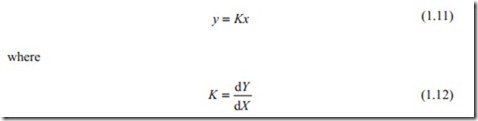Linearization Technique
If there is a continuous nonlinearity in the form of
Feedback Control Theory
In Eqs. (1.10) and (1.9) x, y represent small perturbation from the equilibrium point. Equation (1.10) can be written as
K is constant at an operating point. Throughout this book, the lower case variable represents small perturbation from equilibrium point. This is shown in Fig. 1.3.
Equation (1.8) represents one variable system. For a multivariable system, similar linearized equation can be obtained.
The solution of the governing equation simplifies if Laplace Transform is used.
Related posts:
STEADY STATE EQUIVALENT CIRCUIT AND PERFORMANCE
CONVENTIONAL D.C. MOTORS:MOTIONAL E.M.F.
Loudspeakers:Voice Coil
Signal-carrying switches:Reed switches
Other Digital Audio Devices:DVD and Audio
Wiring Methods for Lighting Circuits:Earthing
Introduction to Actuators Based on Electro-Rheological Fluid
TRANSFORMERS:ANALYSIS OF CIRCUITS CONTAINING IDEAL TRANSFORMERS
Temperature sensors and thermal transducers:Thermal to electrical transducers
Zener Diodes:Voltage regulation with Zener Diodes
Induction motor:Starting Torque and Maximum Torque.
Induction motor:Current/Speed Curve of an Induction Motor
Engine Piston System part7
REAL-TIME OPERATING SYSTEMS:INTERRUPTS