COMPUTER DATA FORMATS

Successful programming requires a precise understanding of data formats. In this section, many common computer data formats are described as they are used with the Intel family of micro- processors. Commonly, data appear as ASCII, Unicode, BCD, signed and unsigned integers, and floating-point numbers (real numbers). Other forms are available, but are not presented here because they are not commonly found.

ASCII and Unicode Data

ASCII (American Standard Code for Information Interchange) data represent alphanumeric characters in the memory of a computer system (see Table 1–8). The standard ASCII code is a 7-bit code, with the eighth and most significant bit used to hold parity in some antiquated systems. If ASCII data are used with a printer, the most significant bits are a 0 for alphanumeric printing and 1 for graphics printing. In the personal computer, an extended ASCII character set is selected by placing a 1 in the leftmost bit. Table 1–9 shows the extended ASCII character set, using code 80H–FFH. The extended ASCII characters store some foreign letters and punctuation, Greek

characters, mathematical characters, box-drawing characters, and other special characters. Note that extended characters can vary from one printer to another. The list provided is designed to be used with the IBM ProPrinter, which also matches the special character set found with most word processors.

The ASCII control characters, also listed in Table 1–8, perform control functions in a computer system, including clear screen, backspace, line feed, and so on. To enter the control codes through the computer keyboard, hold down the Control key while typing a letter. To obtain the control code 01H, type a Control-A; a 02H is obtained by a Control-B, and so on. Note that the control codes appear on the screen, from the DOS prompt, as ^A for Control-A, ^B for Control-B, and so forth. Also note that the carriage return code (CR) is the Enter key on most modem key- boards. The purpose of CR is to return the cursor or print head to the left margin. Another code that appears in many programs is the line feed code (LF), which moves the cursor down one line.

To use Table 1–8 or 1–9 for converting alphanumeric or control characters into ASCII characters, first locate the alphanumeric code for conversion. Next, find the first digit of the hexadecimal ASCII code. Then find the second digit. For example, the capital letter “A” is ASCII code 41H, and the lowercase letter “a” is ASCII code 61H. Many Windows-based applications, since Windows 95, use the Unicode system to store alphanumeric data. This system stores each character as 16-bit data. The codes 0000H–00FFH are the same as standard ASCII code. The remaining codes, 0100H–FFFFH, are used to store all special characters from many worldwide character sets. This allows software written for the Windows environment to be used in many countries around the world. For complete information on Unicode, visit http://www.unicode.org.

ASCII data are most often stored in memory by using a special directive to the assembler program called define byte(s), or DB. (The assembler is a program that is used to program a computer in its native binary machine language.) An alternative to DB is the word BYTE. The DB and BYTE directives, and several examples of their usage with ASCII-coded character strings, are listed in Example 1–18. Notice how each character string is surrounded by apostrophes (’)—never use the quote (”). Also notice that the assembler lists the ASCII-coded value for each character to the left of the character string. To the far left is the hexadecimal memory location where the character string is first stored in the memory system. For example, the character string WHAT is stored beginning at memory address 001D, and the first letter is stored as 57 (W), followed by 68 (H), and so forth. Example 1–19 shows the same three strings defined as String^ character strings for use with Visual C++ Express 2005 and 2008. Note that Visual C++ uses quotes to surround strings. If an earlier version of C++ is used, then the string is defined with a CString for Microsoft Visual C++ instead of a String^. The ^ symbol indicates that String is a member of the garbage collection heap for managing the storage. A garbage collector cleans off the memory system (frees unused memory) when the object falls from visibility or scope in a C++ program and it also prevents memory leaks.

BCD (Binary-Coded Decimal) Data

Binary-coded decimal (BCD) information is stored in either packed or unpacked forms. Packed BCD data are stored as two digits per byte and unpacked BCD data are stored as one digit per byte. The range of a BCD digit extends from 00002 to 10012, or 0–9 decimal. Unpacked BCD data are returned from a keypad or keyboard. Packed BCD data are used for some of the instruc- tions included for BCD addition and subtraction in the instruction set of the microprocessor.

Table 1–10 shows some decimal numbers converted to both the packed and unpacked BCD forms. Applications that require BCD data are point-of-sales terminals and almost any device that performs a minimal amount of simple arithmetic. If a system requires complex arithmetic, BCD data are seldom used because there is no simple and efficient method of performing complex BCD arithmetic.

Example 1–20 shows how to use the assembler to define both packed and unpacked BCD data. Example 1–21 shows how to do this using Visual C++ and char or bytes. In all cases, the convention of storing the least-significant data first is followed. This means that to store 83 into memory, the 3 is stored first, and then followed by the 8. Also note that with packed BCD data, the letter H (hexadecimal) follows the number to ensure that the assembler stores the BCD value rather than a decimal value for packed BCD data. Notice how the numbers are stored in memory as unpacked, one digit per byte; or packed, as two digits per byte.

Byte-Sized Data

Byte-sized data are stored as unsigned and signed integers. Figure 1–14 illustrates both the unsigned and signed forms of the byte-sized integer. The difference in these forms is the weight of the leftmost bit position. Its value is 128 for the unsigned integer and minus 128 for the signed integer. In the signed integer format, the leftmost bit represents the sign bit of the number, as well as a weight of minus 128. For example, 80H represents a value of 128 as an unsigned number; as a signed number, it represents a value of minus 128. Unsigned integers range in value from 00H to FFH (0–255). Signed integers range in value from -128 to 0 to + 127.

Although negative signed numbers are represented in this way, they are stored in the two’s complement form. The method of evaluating a signed number by using the weights of each bit position is much easier than the act of two’s complementing a number to find its value. This is especially true in the world of calculators designed for programmers.

Whenever a number is two’s complemented, its sign changes from negative to positive or positive to negative. For example, the number 00001000 is a +8. Its negative value (-8) is found by two’s complementing the +8. To form a two’s complement, first one’s complement the number. To one’s complement a number, invert each bit of a number from zero to one or from one to zero. Once the one’s complement is formed, the two’s complement is found by adding a one to the one’s complement. Example 1–22 shows how numbers are two’s complemented using this technique.

Another, and probably simpler, technique for two’s complementing a number starts with the rightmost digit. Start by writing down the number from right to left. Write the number exactly as it appears until the first one. Write down the first one, and then invert all bits to its left. Example 1–23 shows this technique with the same number as in Example 1–22.

To store 8-bit data in memory using the assembler program, use the DB directive as in prior examples or char as in Visual C++ examples. Example 1–24 lists many forms of 8-bit numbers stored in memory using the assembler program. Notice in the example that a hexadecimal number is defined with the letter H following the number, and that a decimal number is written as is, without anything special. Example 1–25 shows the same byte data defined for use with a Visual C++ program. In C/C++ the hexadecimal value is preceded by a 0x to indicate a hexadecimal value.

Word-Sized Data

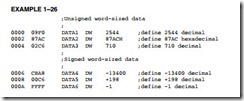
A word (16-bits) is formed with two bytes of data. The least significant byte is always stored in the lowest-numbered memory location, and the most significant byte is stored in the highest. This method of storing a number is called the little endian format. An alternate method, not used with the Intel family of microprocessors, is called the big endian format. In the big endian format, numbers are stored with the lowest location containing the most significant data. The big endian format is used with the Motorola family of microprocessors. Figure 1–15 (a) shows the weights of each bit position in a word of data, and Figure 1–15 (b) shows how the number 1234H appears when stored in the memory locations 3000H and 3001H. The only difference between a signed and an unsigned word in the leftmost bit is position. In the unsigned form, the leftmost bit is unsigned and has a weight of 32,768; in the signed form, its weight is -32,768. As with byte- sized signed data, the signed word is in two’s complement form when representing a negative number. Also, notice that the low-order byte is stored in the lowest-numbered memory location (3000H) and the high-order byte is stored in the highest-numbered location (3001H).

Example 1–26 shows several signed and unsigned word-sized data stored in memory using the assembler program. Example 1–27 shows how to store the same numbers in a Visual C++

program (assuming version 5.0 or newer), which uses the short directive to store a 16-bit integer. Notice that the define word(s) directive, or DW, causes the assembler to store words in the memory instead of bytes, as in prior examples. The WORD directive can also be used to define a word. Notice that the word data is displayed by the assembler in the same form as entered. For example, a l000H is displayed by the assembler as a 1000. This is for our convenience because the number is actually stored in the memory as 00 l0 in two consecutive memory bytes.

Doubleword-Sized Data

Doubleword-sized data requires four bytes of memory because it is a 32-bit number. Doubleword data appear as a product after a multiplication and also as a dividend before a division. In the 80386 through the Core2, memory and registers are also 32 bits in width. Figure 1–16 shows the form used to store doublewords in the memory and the binary weights of each bit position.

When a doubleword is stored in memory, its least significant byte is stored in the lowest numbered memory location, and its most significant byte is stored in the highest-numbered

memory location using the little endian format. Recall that this is also true for word-sized data. For example, 12345678H that is stored in memory locations 00100H–00103H is stored with the 78H in memory location 00100H, the 56H in location 00101H, the 34H in location 00102H, and the 12H in location 00103H.

To define doubleword-sized data, use the assembler directive define doubleword(s), or DD. (You can also use the DWORD directive in place of DD.) Example 1–28 shows both signed and unsigned numbers stored in memory using the DD directive. Example 1–29 shows how to define the same doublewords in Visual C++ using the int directive.

Integers may also be stored in memory that is of any width. The forms listed here are standard forms, but that doesn’t mean that a 256-byte wide integer can’t be stored in the memory. The microprocessor is flexible enough to allow any size of data in assembly language. When non- standard-width numbers are stored in memory, the DB directive is normally used to store them. For example, the 24-bit number 123456H is stored using a DB 56H, 34H, 12H directive. Note that this conforms to the little endian format. This could also be done in Visual C++ using the char directive.

Real Numbers

Because many high-level languages use the Intel family of microprocessors, real numbers are often encountered. A real number, or a floating-point number, as it is often called, contains two parts: a mantissa, significand, or fraction; and an exponent. Figure 1–17 depicts both the 4- and 8-byte forms of real numbers as they are stored in any Intel system. Note that the 4-byte number is called single-precision and the 8-byte form is called double-precision. The form presented here is the same form specified by the IEEE10 standard, IEEE-754, version 10.0. The standard has been adopted as the standard form of real numbers with virtually all programming languages and many applications packages. The standard also applies the data manipulated by the numeric coprocessor in the personal computer. Figure 1–17 (a) shows the single-precision form that contains a sign-bit, an 8-bit exponent, and a 24-bit fraction (mantissa). Note that because applications often require double-precision floating-point numbers [see Figure 1–17 (b)], the Pentium–Core2 with their 64-bit data bus perform memory transfers at twice the speed of the 80386/80486 microprocessors.

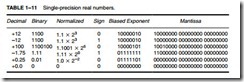
Simple arithmetic indicates that it should take 33 bits to store all three pieces of data. Not true—the 24-bit mantissa contains an implied (hidden) one-bit that allows the mantissa to represent 24 bits while being stored in only 23 bits. The hidden bit is the first bit of the normalized real number. When normalizing a number, it is adjusted so that its value is at least 1, but less than 2.

For example, if 12 is converted to binary (11002), it is normalized and the result is 1.1 * 23. The whole number 1 is not stored in the 23-bit mantissa portion of the number; the 1 is the hidden one-bit. Table 1–11 shows the single-precision form of this number and others.

The exponent is stored as a biased exponent. With the single-precision form of the real number, the bias is 127 (7FH) and with the double-precision form, it is 1023 (3FFH). The bias

and exponent are added before being stored in the exponent portion of the floating-point number. In the previous example, there is an exponent of 23, represented as a biased exponent of 127 + 3 or 130 (82H) in the single-precision form, or as 1026 (402H) in the double-precision form.

There are two exceptions to the rules for floating-point numbers. The number 0.0 is stored as all zeros. The number infinity is stored as all ones in the exponent and all zeros in the mantissa. The sign-bit indicates either a positive or a negative infinity.

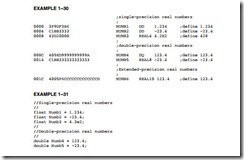
As with other data types, the assembler can be used to define real numbers in both single- and double-precision forms. Because single-precision numbers are 32-bit numbers, use the DD directive or use the define quadword(s), or DQ, directive to define 64-bit double-precision real numbers. Optional directives for real numbers are REAL4, REAL8, and REAL10 for defining single-, double-, and extended precision real numbers. Example 1–30 shows numbers defined in real number format for the assembler. If using the inline assembler in Visual C++ single- precision numbers are defined as float and double-precision numbers are defined as double as shown in Example 1–31. There is no way to define the extended-precision floating-point number for use in Visual C++.

QUESTIONS AND PROBLEMS

1. Who developed the Analytical Engine?

2. The 1890 census used a new device called a punched card. Who developed the punched card?

3. Who was the founder of IBM Corporation?

4. Who developed the first electronic calculator?

5. The first electronic computer system was developed for what purpose?

6. The first general-purpose, programmable computer was called the .

7. The world’s first microprocessor was developed in 1971 by .

8. Who was the Countess of Lovelace?

9. Who developed the first high-level programming language called FLOWMATIC?

10. What is a von Neumann machine?

11. Which 8-bit microprocessor ushered in the age of the microprocessor?

12. The 8085 microprocessor, introduced in 1977, has sold copies.

13. Which Intel microprocessor was the first to address 1M bytes of memory?

14. The 80286 addresses bytes of memory.

15. How much memory is available to the 80486 microprocessor?

16. When did Intel introduce the Pentium microprocessor?

17. When did Intel introduce the Pentium Pro processor?

18. When did Intel introduce the Pentium 4 microprocessor?

19. Which Intel microprocessor addresses 1T of memory?

20. What is the acronym MIPs?

21. What is the acronym CISC?

22. A binary bit stores a(n) or a(n) .

23. A computer K (pronounced kay) is equal to bytes.

24. A computer M (pronounced meg) is equal to K bytes.

25. A computer G (pronounced gig) is equal to M bytes.

26. A computer P (pronounced peta) is equal to T bytes.

27. How many typewritten pages of information are stored in a 4G-byte memory?

28. The first 1M byte of memory in a DOS-based computer system contains a(n) and a(n) area.

29. How large is the Windows application programming area?

30. How much memory is found in the DOS transient program area?

31. How much memory is found in the Windows systems area?

32. The 8086 microprocessor addresses bytes of memory.

33. The Core2 microprocessor addresses bytes of memory.

34. Which microprocessors address 4G bytes of memory?

35. Memory above the first 1M byte is called memory.

36. What is the system BIOS?

37. What is DOS?

38. What is the difference between an XT and an AT computer system?

39. What is the VESA local bus?

40. The ISA bus holds -bit interface cards.

41. What is the USB?

42. What is the AGP?

43. What is the XMS?

44. What is the SATA interface and where is it used in a system?

45. A driver is stored in the area.

46. The personal computer system addresses bytes of I/O space.

47. What is the purpose of the BIOS?

48. Draw the block diagram of a computer system.

49. What is the purpose of the microprocessor in a microprocessor-based computer?

50. List the three buses found in all computer systems.

51. Which bus transfers the memory address to the I/O device or to the memory?

52. Which control signal causes the memory to perform a read operation?

53. What is the purpose of the IORC signal?

54. If the MRDC signal is a logic 0, which operation is performed by the microprocessor?

55. Define the purpose of the following assembler directives:

(a) DB

(b) DQ

(c) DW

(d) DD

56. Define the purpose of the following 32-bit Visual C++ directives:

(a) char

(b) short

(c) int

(d) float

(e) double

57. Convert the following binary numbers into decimal: (a) 1101.01

(b) 111001.0011

(c) 101011.0101

(d) 111.0001

58. Convert the following octal numbers into decimal: (a) 234.5

(b) 12.3

(c) 7767.07

(d) 123.45

(e) 72.72

59. Convert the following hexadecimal numbers into decimal:

(a) A3.3

(b) 129.C

(c) AC.DC

(d) FAB.3

(e) BB8.0D

60. Convert the following decimal integers into binary, octal, and hexadecimal:

(a) 23

(b) 107

(c) 1238

(d) 92

(e) 173

61. Convert the following decimal numbers into binary, octal, and hexadecimal: (a) 0.625

(b) .00390625

(c) .62890625

(d) 0.75

(e) .9375

62. Convert the following hexadecimal numbers into binary-coded hexadecimal code (BCH):

(a) 23

(b) AD4

(c) 34.AD

(d) BD32

(e) 234.3

63. Convert the following binary-coded hexadecimal numbers into hexadecimal: (a) 1100 0010

(b) 0001 0000 1111 1101

(c) 1011 1100

(d) 0001 0000

(e) 1000 1011 1010

64. Convert the following binary numbers to the one’s complement form: (a) 1000 1000

(b) 0101 1010

(c) 0111 0111

(d) 1000 0000

65. Convert the following binary numbers to the two’s complement form:

(a) 1000 0001

(b) 1010 1100

(c) 1010 1111

(d) 1000 0000

66. Define byte, word, and doubleword.

67. Convert the following words into ASCII-coded character strings:

(a) FROG

(b) Arc

(c) Water

(d) Well

68. What is the ASCII code for the Enter key and what is its purpose?

69. What is the Unicode?

70. Use an assembler directive to store the ASCII-character string ‘What time is it?’ in the memory.

71. Convert the following decimal numbers into 8-bit signed binary numbers:

(a) +32

(b) -12

(c) +100

(d) -92

72. Convert the following decimal numbers into signed binary words:

(a) +1000

(b) -120

(c) +800

(d) -3212

73. Use an assembler directive to store byte-sized -34 into the memory.

74. Create a byte-sized variable called Fred1 and store a -34 in it in Visual C++.

75. Show how the following 16-bit hexadecimal numbers are stored in the memory system (use the standard Intel little endian format):

(a) 1234H

(b) A122H

(c) B100H

76. What is the difference between the big endian and little endian formats for storing numbers that are larger than 8 bits in width?

77. Use an assembler directive to store a 123A hexadecimal into memory.

78. Convert the following decimal numbers into both packed and unpacked BCD forms:

(a) 102

(b) 44

(c) 301

(d) 1000

79. Convert the following binary numbers into signed decimal numbers:

(a) 10000000

(b) 00110011

(c) 10010010

(d) 10001001

80. Convert the following BCD numbers (assume that these are packed numbers) to decimal numbers:

(a) 10001001

(b) 00001001

(c) 00110010

(d) 00000001

81. Convert the following decimal numbers into single-precision floating-point numbers:

(a) +1.5

(b) –10.625

(c) +100.25

(d) –1200

82. Convert the following single-precision floating-point numbers into decimal numbers:

(a) 0 10000000 11000000000000000000000

(b) 1 01111111 00000000000000000000000

(c) 0 10000010 10010000000000000000000

83. Use the Internet to write a short report about any one of the following computer pioneers:

(a) Charles Babbage

(b) Konrad Zuse

(c) Joseph Jacquard

(d) Herman Hollerith

84. Use the Internet to write a short report about any one of the following computer languages:

(a) COBOL

(b) ALGOL

(c) FORTRAN

(d) PASCAL

85. Use the Internet to write a short report detailing the features of the Itanium 2 microprocessor.

86. Use the Internet to detail the Intel 45 nm (nanometer) fabrication technology.

SUMMARY

1. The mechanical computer age began with the advent of the abacus in 500 B.C. This first mechanical calculator remained unchanged until 1642, when Blaise Pascal improved it. An early mechanical computer system was the Analytical Engine developed by Charles Babbage in 1823. Unfortunately, this machine never functioned because of the inability to create the necessary machine parts.

2. The first electronic calculating machine was developed during World War II by Konrad Zuse, an early pioneer of digital electronics. His computer, the Z3, was used in aircraft and missile design for the German war effort.

3. The first electronic computer, which used vacuum tubes, was placed into operation in 1943 to break secret German military codes. This first electronic computer system, the Colossus, was invented by Alan Turing. Its only problem was that the program was fixed and could not be changed.

4. The first general-purpose, programmable electronic computer system was developed in 1946 at the University of Pennsylvania. This first modern computer was called the ENIAC (Electronics Numerical Integrator and Calculator).

5. The first high-level programming language, called FLOWMATIC, was developed for the UNIVAC I computer by Grace Hopper in the early 1950s. This led to FORTRAN and other early programming languages such as COBOL.

6. The world’s first microprocessor, the Intel 4004, was a 4-bit microprocessor—a programmable controller on a chip—that was meager by today’s standards. It addressed a mere 4096 4-bit memory locations. Its instruction set contained only 45 different instructions.

7. Microprocessors that are common today include the 8086/8088, which were the first 16-bit microprocessors. Following these early 16-bit machines were the 80286, 80386, 80486, Pentium, Pentium Pro, Pentium II, Pentium III, Pentium 4, and Core2 processors. The architecture has changed from 16 bits to 32 bits and, with the Itanium, to 64 bits. With each newer version, improvements followed that increased the processor’s speed and performance. From all indications, this process of speed and performance improvement will continue, although the performance increases may not always come from an increased clock frequency.

8. The DOS-based personal computers contain memory systems that include three main areas: TPA (transient program area), system area, and extended memory. The TPA hold: application programs, the operating system, and drivers. The system area contains memory used for video display cards, disk drives, and the BIOS ROM. The extended memory area is only available to the 80286 through the Core2 microprocessor in an AT-style or ATX-style personal computer system. The Windows-based personal computers contain memory systems that include two main areas: TPA and systems area.

9. The 8086/8088 address 1M byte of memory from locations 00000H–FFFFFH. The 80286 and 80386SX address 16M bytes of memory from locations 000000H–FFFFFFH. The 80386SL addresses 32M bytes of memory from locations 0000000H–1FFFFFFH. The 80386DX through the Core2 address 4G bytes of memory from locations 00000000H–FFFFFFFFH. In addition, the Pentium Pro through the Core2 can operate with a 36-bit address and access up to 64G bytes of memory from locations 000000000H–FFFFFFFFFH. A Pentium 4 or Core2 operating with 64-bit extensions addresses memory from locations 0000000000H– FFFFFFFFFFH for 1T byte of memory.

10. All versions of the 8086 through the Core2 microprocessors address 64K bytes of I/O address space. These I/O ports are numbered from 0000H to FFFFH with I/O ports 0000H–03FFH reserved for use by the personal computer system. The PCI bus allows ports 0400H–FFFFH.

11. The operating system in early personal computers was either MSDOS (Microsoft disk operating system) or PCDOS (personal computer disk operating system from IBM). The operating system performs the task of operating or controlling the computer system, along with its I/O devices. Modern computers use Microsoft Windows in place of DOS as an operating system.

12. The microprocessor is the controlling element in a computer system. The microprocessor performs data transfers, does simple arithmetic and logic operations, and makes simple decisions. The microprocessor executes programs stored in the memory system to perform com- plex operations in short periods of time.

13. All computer systems contain three buses to control memory and I/O. The address bus is used to request a memory location or I/O device. The data bus transfers data between the microprocessor and its memory and I/O spaces. The control bus controls the memory and I/O, and requests reading or writing of data. Control is accomplished with IORC (I/O read control), IOWC (I/O write control), MRDC (memory read control), and MWTC (memory write control).

14. Numbers are converted from any number base to decimal by noting the weights of each position. The weight of the position to the left of the radix point is always the units position in any number system. The position to the left of the units position is always the radix times one. Succeeding positions are determined by multiplying by the radix. The weight of the position to the right of the radix point is always determined by dividing by the radix.

15. Conversion from a whole decimal number to any other base is accomplished by dividing by the radix. Conversion from a fractional decimal number is accomplished by multiplying by the radix.

16. Hexadecimal data are represented in hexadecimal form or in a code called binary-coded hexadecimal (BCH). A binary-coded hexadecimal number is one that is written with a 4-bit binary number that represents each hexadecimal digit.

17. The ASCII code is used to store alphabetic or numeric data. The ASCII code is a 7-bit code; it can have an eighth bit that is used to extend the character set from 128 codes to 256 codes. The carriage return (Enter) code returns the print head or cursor to the left margin. The line feed code moves the cursor or print head down one line. Most modern applications use Unicode, which contains ASCII at codes 0000H–00FFH.

18. Binary-coded decimal (BCD) data are sometimes used in a computer system to store deci- mal data. These data are stored either in packed (two digits per byte) or unpacked (one digit per byte) form.

19. Binary data are stored as a byte (8 bits), word (16 bits), or doubleword (32 bits) in a com- puter system. These data may be unsigned or signed. Signed negative data are always stored in the two’s complement form. Data that are wider than 8 bits are always stored using the little endian format. In 32-bit Visual C++ these data are represented with char (8 bits), short (16 bits) and int (32 bits).

20. Floating-point data are used in computer systems to store whole, mixed, and fractional numbers. A floating-point number is composed of a sign, a mantissa, and an exponent.

21. The assembler directives DB or BYTE define bytes, DW or WORD define words, DD or DWORD define doublewords, and DQ or QWORD define quadwords.

NUMBER SYSTEMS

The use of the microprocessor requires a working knowledge of binary, decimal, and hexadecimal numbering systems. This section of the text provides a background for those who are unfamiliar with these numbering systems. Conversions between decimal and binary, decimal and hexadecimal, and binary and hexadecimal are described.

Digits

Before numbers are converted from one number base to another, the digits of a number system must be understood. Early in our education, we learned that a decimal (base 10) number is constructed with 10 digits: 0 through 9. The first digit in any numbering system is always zero. For example, a base 8 (octal) number contains 8 digits: 0 through 7; a base 2 (binary) number contains 2 digits: 0 and 1. If the base of a number exceeds 10, the additional digits use the letters of the alphabet, beginning with an A. For example, a base 12 number contains 10 digits: 0 through 9, followed by A for 10 and B for 11. Note that a base 10 number does contain a 10 digit, just as a base 8 number does not contain an 8 digit. The most common numbering systems used with computers are decimal, binary, and hexadecimal (base 16). (Many years ago octal numbers were popular.) Each of these number systems are described and used in this section the chapter.

Positional Notation

Once the digits of a number system are understood, larger numbers are constructed by using positional notation. In grade school, we learned that the position to the left of the units position is the tens position, the position to the left of the tens position is the hundreds position, and so forth. (An example is the decimal number 132: This number has 1 hundred, 3 tens, and 2 units.) What probably was not learned was the exponential value of each position: The units position has a weight of 100, or 1; the tens position has weight of 101, or 10; and the hundreds position has a weight of 102, or 100. The exponential powers of the positions are critical for understanding numbers in other numbering systems. The position to the left of the radix (number base) point, called a decimal point only in the decimal system, is always the units position in any number sys- tem. For example, the position to the left of the binary point is always 20, or 1; the position to the left of the octal point is 80, or 1. In any case, any number raised to its zero power is always 1, or the units position.

The position to the left of the units position is always the number base raised to the first power; in a decimal system, this is 101, or 10. In a binary system, it is 21, or 2; and in an octal system, it is 8l, or 8. Therefore, an 11 decimal has a different value from an 11 binary. The decimal number is composed of 1 ten plus 1 unit, and has a value of 11 units; while the binary number 11 is composed of 1 two plus 1 unit, for a value of 3 decimal units. The 11 octal has a value of 9 decimal units.

In the decimal system, positions to the right of the decimal point have negative powers. The first digit to the right of the decimal point has a value of 10-1, or 0.1. In the binary system the first digit to the right of the binary point has a value of 2-1, or 0.5. In general, the principles that apply to decimal numbers also apply to numbers in any other number system.

Example 1–1 shows 110.101 in binary (often written as 110.1012). It also shows the power and weight or value of each digit position. To convert a binary number to decimal, add weights of each digit to form its decimal equivalent. The 110.1012 is equivalent to a 6.625 in decimal (4 + 2 + 0.5 + 0.125). Notice that this is the sum of 22 (or 4) plus 21 (or 2), but 20 (or 1) is not added because there are no digits under this position. The fraction part is com- posed of 2-1 (.5) plus 2-3 (or .125), but there is no digit under the 2-2 (or .25) so .25 is not added.

Suppose that the conversion technique is applied to a base 6 number, such as 25.26. Example 1–2 shows this number placed under the powers and weights of each position. In the example, there is a 2 under 61, which has a value of 1210 (2 * 6), and a 5 under 60, which has a value of 5 (5 * 1). The whole number portion has a decimal value of 12 + 5, or 17. The number to the right of the hex point is a 2 under 6-1, which has a value of .333 (2 * .167). The number 25.26, therefore, has a value of 17.333.

Conversion to Decimal

The prior examples have shown that to convert from any number base to decimal, determine the weights or values of each position of the number, and then sum the weights to form the decimal equivalent. Suppose that a 125.78 octal is converted to decimal. To accomplish this conversion, first write down the weights of each position of the number. This appears in Example 1–3. The value of 125.78 is 85.875 decimal, or 1 * 64 plus 2 * 8 plus 5 * 1 plus 7 * .125.

Notice that the weight of the position to the left of the units position is 8. This is 8 times 1. Then notice that the weight of the next position is 64, or 8 times 8. If another position existed, it would be 64 times 8, or 512. To find the weight of the next higher-order position, multiply the weight of the current position by the number base (or 8, in this example). To calculate the weights of position to the right of the radix point, divide by the number base. In the octal system, the position immediately to the right of the octal point is 1/8, or .125. The next position is .125/8, or .015625, which can also be written as 1/64. Also note that the number in Example 1–3 can also be written as the decimal number 857/8.

Example 1–4 shows the binary number 11011.0111 written with the weights and powers of each position. If these weights are summed, the value of the binary number converted to decimal is 27.4375.

It is interesting to note that 2-1 is also 1/2, 2-2 is 1/4, and so forth. It is also interesting to note that 2-4 is 1/16, or .0625. The fractional part of this number is 7/16 or .4375 decimal. Notice that 0111 is a 7 in binary code for the numerator and the rightmost one is in the 1/16 position for the denominator. Other examples: The binary fraction of .101 is 5/8 and the binary fraction of .001101 is 13/64.

Hexadecimal numbers are often used with computers. A 6A.CH (H for hexadecimal) is illustrated with its weights in Example 1–5. The sum of its digits is 106.75, or 1063⁄4. The whole number part is represented with 6 * 16 plus 10 1A2 * 1. The fraction part is 12 (C) as a numerator and 16 (16-1) as the denominator, or 12/16, which is reduced to 3/4.

Conversion from Decimal

Conversions from decimal to other number systems are more difficult to accomplish than con- version to decimal. To convert the whole number portion of a number to decimal, divide by 1 radix. To convert the fractional portion, multiply by the radix.

Whole Number Conversion from Decimal. To convert a decimal whole number to another number system, divide by the radix and save the remainders as significant digits of the result. An algorithm for this conversion as is follows:

1. Divide the decimal number by the radix (number base).

2. Save the remainder (first remainder is the least significant digit).

3. Repeat steps 1 and 2 until the quotient is zero.

For example, to convert a 10 decimal to binary, divide it by 2. The result is 5, with a remain- der of 0. The first remainder is the units position of the result (in this example, a 0). Next divide the 5 by 2. The result is 2, with a remainder of 1. The 1 is the value of the twos (21) position. Continue the division until the quotient is a zero. Example 1–6 shows this conversion process. The result is written as 10102 from the bottom to the top.

Converting from a Decimal Fraction. Conversion from a decimal fraction to another number base is accomplished with multiplication by the radix. For example, to convert a decimal fraction into binary, multiply by 2. After the multiplication, the whole number portion of the result is saved as a significant digit of the result, and the fractional remainder is again multiplied by the radix. When the fraction remainder is zero, multiplication ends. Note that some numbers are never-ending (repetend). That is, a zero is never a remainder. An algorithm for conversion from a decimal fraction is as follows:

1. Multiply the decimal fraction by the radix (number base).

2. Save the whole number portion of the result (even if zero) as a digit. Note that the first result is written immediately to the right of the radix point.

3. Repeat steps 1 and 2, using the fractional part of step 2 until the fractional part of step 2 is zero.

Suppose that a .125 decimal is converted to binary. This is accomplished with multiplications by 2, as illustrated in Example 1–9. Notice that the multiplication continues until the fractional remainder is zero. The whole number portions are written as the binary fraction (0.001) in this example.

Binary-Coded Hexadecimal

Binary-coded hexadecimal (BCH) is used to represent hexadecimal data in binary code. A binary-coded hexadecimal number is a hexadecimal number written so that each digit is repre- sented by a 4-bit binary number. The values for the BCH digits appear in Table 1–7.

Hexadecimal numbers are represented in BCH code by converting each digit to BCH code with a space between each coded digit. Example 1–12 shows a 2AC converted to BCH code. Note that each BCH digit is separated by a space.

The purpose of BCH code is to allow a binary version of a hexadecimal number to be written in a form that can easily be converted between BCH and hexadecimal. Example 1–13 shows a BCH coded number converted back to hexadecimal code.

EXAMPLE 1–13

1000 0011 1101 . 1110 = 83D.E

Complements

At times, data are stored in complement form to represent negative numbers. There are two systems that are used to represent negative data: radix and radix – 1 complements. The earliest system was the radix -1 complement, in which each digit of the number is subtracted from the radix -1 to gen- erate the radix -1 complement to represent a negative number.

Example 1–14 shows how the 8-bit binary number 01001100 is one’s (radix -1) comple- mented to represent it as a negative value. Notice that each digit of the number is subtracted from one to generate the radix -1 (one’s) complement. In this example, the negative of 01001100 is 10110011. The same technique can be applied to any number system, as illustrated in Example 1–15, in which the fifteen’s (radix -1) complement of a 5CD hexadecimal is com- puted by subtracting each digit from a fifteen.

Today, the radix -1 complement is not used by itself; it is used as a step for finding the radix complement. The radix complement is used to represent negative numbers in modem computer systems. (The radix -1 complement was used in the early days of computer technology.) The main problem with the radix -1 complement is that a negative or a positive zero exists; in the radix complement system, only a positive zero can exist.

To form the radix complement, first find the radix -1 complement, and then add a one to the result. Example 1–16 shows how the number 0100 1000 is converted to a negative value by two’s (radix) complementing it.

To prove that a 0100 1000 is the inverse (negative) of a 1011 1000, add the two together to form an 8-digit result. The ninth digit is dropped and the result is zero because a 0100 1000 is a positive 72, while a 1011 1000 is a negative 72. The same technique applies to any number system. Example 1–17 shows how the inverse of a 345 hexadecimal is found by first fifteen’s complement- ing the number, and then by adding one to the result to form the sixteen’s complement. As before, if the original 3-digit number 345 is added to the inverse of CBB, the result is a 3-digit 000. As before, the fourth bit (carry) is dropped. This proves that 345 is the inverse of CBB. Additional information about one’s and two’s complements is presented with signed numbers in the next section of the text.