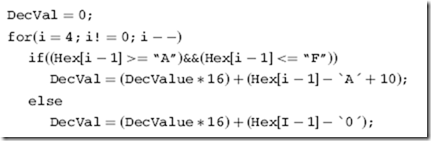Number Systems : Base 16 or Hexadecimal Numbers

Number Systems

Working through the book to this point, you should be comfortable with combining multiple single bit values together in a variety of different ways to perform different combinatorial circuit functions. Along with being able to meet the basic requirements, you should be able to optimize the circuit to the fewest number of gates that is available within the technology that you are going to use. This skill is very useful in itself, but it is only scratching the surface of what can be done with digital electronics; most data consists of more than a single bit (which can have only two values) to process, and working with multiple single bits of data can be cumbersome. What is needed is a methodology for combining bits together so they can represent larger values that can be simply expressed.

The solution to this issue is to combine bits in exactly the same way as a 10-value character is combined to produce the decimal numbers that you are familiar with. While on the surface, combining bits does not seem to be directly analogous to decimal numbers, by using the same method that decimal numbers are produced, multi-bit numbers (which are most often described as ‘‘binary’’) numbers can be produced.

In primary school, you learned that the four-digit number ‘‘1,234’’ was built out of four digits, any of which could have the 10 values ‘‘0’’, ‘‘1’’, ‘‘2’’,‘‘3’’, ‘‘4’’, ‘‘5’’, ‘‘6’’, ‘‘7’’, ‘‘8’’ and ‘‘9’’. When listing the different values for a digit, zero is stated because the number ‘‘10’’ is actually a two digit number. The number of different values for each digit is referred to as its ‘‘base’’ or ‘‘radix’’. It is important to note that the first value is always zero and the last value is the base minus one.

When expressing each digit, its value was stated by the ‘‘column’’ it was in (‘‘ones’’, ‘‘tens’’, ‘‘hundreds’’, ‘‘thousands’’, etc.). For example, the second column of ‘‘1,234’’ is the ‘‘hundreds’’ column and in 1234, there are two hundreds.

In high school, you would have been introduced to the concept of exponents and instead of expressing each digit in the number by the column, you would express it by the digit multiplier. So, 1,234 could now be written out as:

The beauty of expressing a number in this way is that each digit’s multiplier is mathematically defined as a power of the base. Using this format, it is possible to create a numbering system using single bits to represent ‘‘binary’’ numbers.

For example, four bits could be put together with the bit containing the least significant digit labelled ‘‘Bit0’’, the second least significant as ‘‘Bit1’’, the second most significant as ‘‘Bit2’’ and the most significant as ‘‘Bit3’’. The term significance when applied to bits is used to express the magnitude of the bit’s multiplier. For example, Bit0, which is multiplied by 20 or 1, has less significance than Bit3 which is multiplied by 23 or 8.

Using the same exponent format as was used to define the decimal number 1,234, the four-bit binary number could be defined as:

and written out in a similar format to a decimal number. Collectively, the number is written out as a series of ones and zeros, in a similar manner to that of a decimal number.

Many books go into great length trying to explain how to convert a decimal number to a binary number. I won’t go into the same amount of detail because the algorithm to do this is really quite simple: you simply start at some most power of two and work your way down, writing out a ‘‘1’’ for each time the subtraction the power of two results in a positive number or zero and a ‘‘0’’ when the difference is negative.

Written out as part of a ‘‘C’’ program, converting a decimal number to a character four-bit binary number is accomplished by the following statements:

Note that I start at ‘‘4’’ and subtract one for the actual bit value in the example code above.

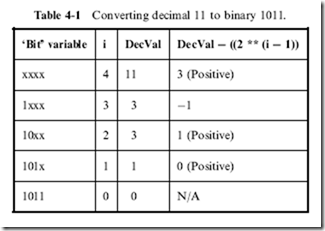
Demonstrating the algorithm, consider the case where you wanted to express the decimal number ‘‘11’’ as a four-bit decimal. In Table 4-1, I have listed each step of the program with the variable values at each step.

Converting binary numbers to decimal is very easy because the power of two of each digit that has a value of ‘‘1’’ are summed together. The ‘‘C’’ code

to convert a value in ‘‘Bit’’ to a decimal value is:

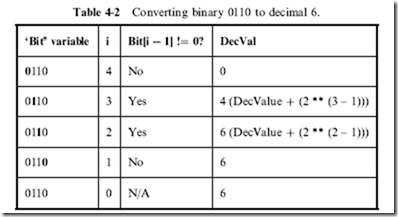
In Table 4-2, I have listed the process of converting the binary number 0110 to decimal and you should note that I have highlighted the bit that is being tested.

Before going on, I would like to point out that there can be a lot of confusion with regards to using binary numbers with decimal numbers or numbers of different bases. To eliminate the confusion, you should always identify the binary numbers by placing a percentage sign (‘‘%’’) or surrounding it with the letter ‘‘B’’ and two single quotes (‘‘ ’ ’’). Using these conventions, the bit pattern converted in Table 4-1 would be written out as %0110 or B’0110’. The % character put before a binary number is a common assembly language programming convention. The letter ‘‘B’’ and the single quotes around the number is the format used in ‘‘C’’ programming and will be the convention that I use in this book.

Another area of confusion with regards to binary numbers is how they are broken up for easier reading. Each group of three digits in a decimal number is usually separated from other groups of digits by use of a comma (‘‘,’’ in North America and a period or dot (‘‘.’’) in Europe and other parts of the world). When working with binary numbers, instead of separating each three digit group with a punctuation character, it is customary to use a blank to separate four digit groups. Using the conventions outlined here, the eight bit number 10111101 would be written out as:

This is the binary number format convention that I will use for the rest of the book.

Base 16 or Hexadecimal Numbers

As I will show in this and the next section, having programming experience is a two-edged sword – it will help you understand certain concepts (such as the ‘‘bit’’ and some data structures like the ones presented in this and the next section), but it will blind you to other opportunities. The goal of these sections is to illustrate how bits can be grouped together to make your design efforts more efficient as well as making it easier for you to both see possibilities for the design and articulate them to other people.

Creating binary numbers from groups of bits, as I demonstrated in the introduction to this chapter, is quite easy to do, but can be very cumbersome to write out as well as transfer correctly. You may also have difficulty in figuring out exactly how to express the number, asking should it be passed along starting from the most significant or least significant bit. At the end of this chapter’s introduction, I left you with the number B’1011 1101’ and you should agree that telling somebody its value is quite cumbersome; for example, you might say something like, ‘‘The eight bit, binary number, starting with the most significant bit is one, zero, one, one, one, one, zero and one.’’

It is much more efficient to combine multiple bits together into a single entity or digit.

The most popular way of doing this is to combine four bits together as a ‘‘hexadecimal’’ digit which has 16 different values. This numbering system has a base of 16. If you are familiar with programming, chances are you are familiar with hexadecimal digits (which is often contracted to the term ‘‘hex’’), which I have listed out with their decimal and binary equivalents in Table 4-3.

To create a way of expressing the 16 values, the first 10 hexadecimal values are the same as the 10 decimal number values, with the following six being given letter codes. This is why I included the ‘‘phonetic’’ values for the hexadecimal values greater than 9; the letter names ‘‘B’’, ‘‘C’’ and ‘‘D’’ can be easily confused, but their phonetic representations are much clearer.

Table 4-3 Hexadecimal digits with binary, decimal equivalents and phonetic values.

I tend to place a lot of importance to using conventions when expressing letters. You may be tempted to make up your own letter codes or use the aviation phonetic alphabet (Table 4-4) when communicating hexadecimal values to other people (‘‘AF’’ could be ‘‘Apple-Frank’’ or ‘‘Alpha-Foxtrot’’ instead of ‘‘Able-Fox’’). I would like to discourage this for two reasons: the first is that the person you are talking to will have to mentally convert your words into letters and then hex digits – this process is complicated when unexpected words are used. Secondly, I prefer using the phonetic codes in Table 4-3 for hex values and the aviation phonetic codes for letter codes.

Multi-digit hexadecimal numbers are written out in a similar way as decimal or binary numbers with each digit multiplied by 16 to the power of the number of value’s position. For a 16 bit number (four hexadecimal digits), the digit multipliers are listed below:

To indicate a hex number, you should use one of the programming conventions, such as putting the prefix ‘‘0x0’’ or ‘‘$’’ at the start of the hexadecimal

Table 4-4 Aviation phonetic codes.

value. The same formatting convention used with binary numbers (X’##’, where ‘‘##’’ are the hex digits) could also be used. For this book, I will be expressing hexadecimal numbers in the format 0x0## which is visually very different from binary numbers, which should help to immediately differentiate them.

To convert a decimal number to a character 16 bit hexadecimal number, you can use the ‘‘C’’ algorithm shown below. Note that I have used the C modulo (‘‘%’’) operation which returns the remainder from an integer division operation and not its dividend.

Going the other way, to convert a four hexadecimal digit number to decimal you can use the algorithm:

Many books provide a conversion table between binary, hexadecimal and decimal numbers, but I would like you to be familiar with the conversion algorithms written out above as well as buy yourself an inexpensive scientific calculator which has ability to convert between base systems. The ability to convert between the base systems is actually quite simple and available in many basic scientific calculators which cost $10 or less. Understanding how to convert between base systems and having an inexpensive calculator will enable you to perform the conversions faster and with more flexibility than using a table, which is limited in the number of different values it can present.

If you are familiar with numbers in different languages, then you will know that the prefix ‘‘hex’’ actually refers to the number ‘‘six’’ and not ‘‘16’’. The actual prefix for 16 is the term ‘‘sex’’ and in the early days of computers, this was (obviously) a source of some amusement. When IBM introduced the System/360, in the early 1960s, the company was uncomfortable with releasing something that was programmed in ‘‘sexadecimal’’, fearing that it might upset some users. To avoid any controversy, all documentation for the System/360 was written using the 16 bit ‘‘hexadecimal’’ numbering system presented here. The System/360 was a wild success, becoming the first ‘‘computer for the masses’’ and many people’s first experience in program- ming and electronics. The term ‘‘hexadecimal’’ became the popular term for 16 bit numbers and displaced the more correct ‘‘sexadecimal.’’