Subtraction and Negative Numbers
As you might expect, binary subtraction has many of the same issues as addition, along with a few complexities that can make it harder to work with. In this section, I will introduce some of the issues in implementing a practical ‘‘subtracter’’ as well as look at some ways in which subtraction can be implemented easily with an existing addition circuit.
To make sure we’re talking the same language, I want to define the terms that I will be using to describe the different parts of the subtraction operation. The ‘‘horizontal’’ arithmetic equation:
The ‘‘minuend’’ and ‘‘subtrahend’’ terms are probably something that you forgot that you learned from grade school. I use them here because they are less awkward than referring to them as the ‘‘value to be subtracted from’’ and the ‘‘value subtracted’’. The term ‘‘difference’’ as being the result of a subtraction operation is generally well understood and accepted.
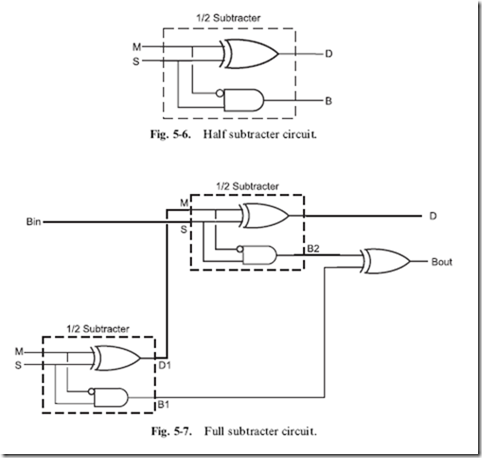
When you carry out subtraction operations, you do it in a manner that is very similar to how you carry out addition; each digit is done individually and if the digit result is less than zero, the base value is ‘‘borrowed’’ from the next significant digit. With the assumption that subtraction works the same way as addition, you could create a ‘‘half subtracter’’, which is analogous to the half adder and could be defined by the truth table shown in Table 5-5
The ‘‘difference’’ bit is simply the minuend and subtrahend XORed together, while the ‘‘borrow’’ bit (decrementing the next significant digit) is only true if the minuend is 0 and the subtrahend is 1. The borrow bit can be defined as the inverted minuend ANDed with the subtrahend. The equations
Table 5-5 ‘‘Half subtracter’’ defining truth table.
|
Minuend |
Subtrahend |
Difference |
Borrow |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
for the half subtracter are listed below and the subtracter building block is shown in Fig. 5-6.
The small circle on the single input indicates that the value is inverted before being passed into the gate. This convention avoids the need for putting a full inverter symbol in the wiring diagram of a digital circuit and is often used in chip datasheets to indicate inverted inputs to complex internal functions.
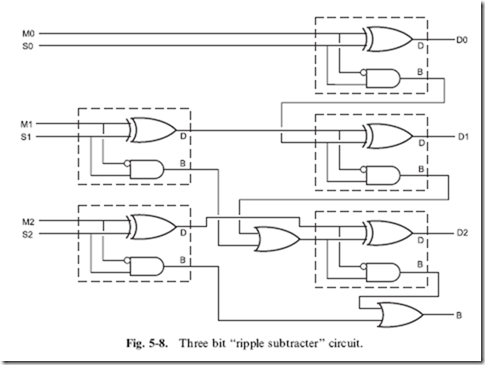
Two half subtracters can be combined into a ‘‘full subtracter’’, just as two half adders can be combined to form a full adder (Fig. 5-7). In Fig. 5-7, I have labeled the two half subtracters, so that their operation can be listed in Table 5-6, to test the operation of the full subtracter.
Table 5-6 Full subtracter operation truth table.
|
Bin |
Minuend (‘‘M’’) |
Subtrahend (‘‘S’’) |
D1 |
B1 |
D |
B2 |
Bout |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
|
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
|
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
|
|
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
|
|
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
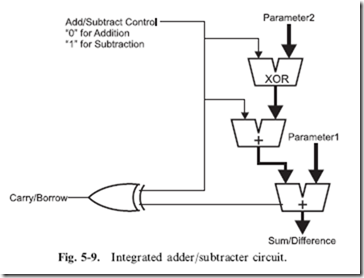
Like the ripple adder, full subtracters can be chained together to create a multi-bit subtracter circuit (Fig. 5-8) and a ‘‘borrow look-ahead’’ (to coin a phrase) subtracter could be designed, but instead of going through the pain of designing one, there is another option and that is to add the negative of the subtrahend to the minuend.
In the introduction to this chapter, I introduced the idea of negative
numbers as being the value being subtracted from an arbitrary large number and showed an example that produced ‘‘-5’’ in a universe where infinity was equal to one million. When you first went through this example, you might have thought that this was an interesting mathematical diversion and an illustration as to how negative and positive numbers converge when they approach infinity. This concept, while seemingly having little application in the ‘‘real world’’, is very useful in the digital domain.
In the digital domain, the term ‘‘infinity’’ can be replaced with ‘‘word size’’ and if the most significant bit of the word is considered to be the ‘‘sign’’ bit, positive and negative numbers can be expressed easily. In Table 5-7, I have listed the decimal, hex as well as the positive and negative values which take into account that a negative number can be written as:
This negative value is known as a ‘‘two’s complement’’ negative number and is the most commonly used negative bit format used. There is a ‘‘one’s
complement’’ number format, but it does not avail itself as efficiently as two’s complement to allow for easier subtraction and addition of negative numbers.
Looking at the formula above, you are probably confused as to why it would be used because it requires both a subtraction operation as well as an addition operation to carry out one subtraction operation. Negating a number in two’s complement format does not actually require a subtraction operation; it can be done by inverting each bit (XORing each bit with 1) and then incrementing the result. Using the values of Table 5-7, you can demonstrate how a positive value is negated.
For example, to negate the value ‘‘5’’, the following steps are used:
1. Each bit of the number is XORed with ‘‘1’’. B’0101’ becomes B’1010’.
2. The XORed result is incremented. B’1010’ becomes B’1011’, which is ‘‘-5’’.
The opposite is also true: the individual bits can be inverted and the result incremented to convert a negative two’s complement value to a positive.
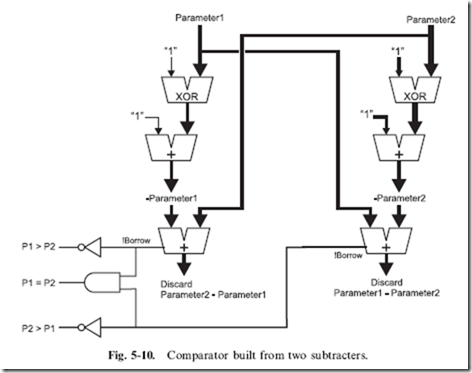
Once the value has been negated, it can be simply added to the other parameter, as I show in Fig. 5-9. There are three things that you should be
Table 5-7 Different ways of representing a four bit number.
|
Binary value |
Decimal value |
Hex value |
Two’s complement value |
|
B’0000’ |
0 |
0x00 |
0 |
|
B’0001’ |
1 |
0x01 |
1 |
|
B’0010’ |
2 |
0x02 |
2 |
|
B’0011’ |
3 |
0x03 |
3 |
|
B’0100’ |
4 |
0x04 |
4 |
|
B’0101’ |
5 |
0x05 |
5 |
|
B’0110’ |
6 |
0x06 |
6 |
|
B’0111’ |
7 |
0x07 |
7 |
|
B’1000’ |
8 |
0x08 |
-8 |
|
B’1001’ |
9 |
0x09 |
-7 |
|
B’1010’ |
10 |
0x0A |
-6 |
|
B’1011’ |
11 |
0x0B |
-5 |
|
B’1100’ |
12 |
0x0C |
-4 |
|
B’1101’ |
13 |
0x0D |
-3 |
|
B’1110’ |
14 |
0x0E |
-2 |
|
B’1111’ |
15 |
0x0F |
-1 |
aware of before leaving this section. The first is the use of the ‘‘V’’ shaped mathematical function symbols in Fig. 5-9; these symbols indicate that two parameters are brought together to form one output. I use this symbol when a group of bits (not just one) are passing through the same operation.
You might be wondering why instead of simply inverting the individual bits of the value to be converted to a negative two’s complement value, I XOR the bits with the value 1. The reason for doing this is in the interests
of practicality and looking ahead. In Fig. 5-9, I show a circuit in which two parameters can be added together or one can be subtracted by the other – the ‘‘switch’’ control for which operation is selected. If a 1 is passed to the ‘‘Parameter2’’ circuitry, each bit of Parameter2 is XORed with 1, inverting each bit and a 1 is passed to the Parameter2 adder, which increments the value. If a zero is passed to the Parameter2 circuitry, the bits of Parameter2 are not inverted and zero is added to the output of the XOR function, resulting in an unchanged value of Parameter2 being passed to the adder with Parameter1. To net it out, if a ‘‘1’’ is passed to this circuit, Parameter2 is subtracted from Parameter1; if a ‘‘0’’ is passed to the circuit, the two parameters are added together.
The last point to note is that the ‘‘carry’’ output of the final adder is a negated ‘‘borrow’’ output when the subtraction operation is taking place. To integrate the operation of the ‘‘carry/borrow’’ bit with the add/subtract switch bit, this bit is set when a carry or borrow of the next significant word is required, regardless of the operation.
Magnitude Comparators and Bus Nomenclature
Along with being able to add and subtract binary values, you will find the need to compare binary values to determine whether or not a value is less
than, equal to or greater than another value. Just as if this were a programming requirement, to test two binary values together, you would subtract one from the other and look at the results. An important issue when comparing a value made up of multiple bits is specifying how it is to be represented in logic drawings and schematic diagrams. In the previous section I touched on both these issues, in this section, I want to expand upon them and help you to understand a bit more about them.
When you are comparing two binary values, you are comparing the magnitude of the values, which is where the term ‘‘magnitude comparator’’ comes from. The typical magnitude comparator consists of two subtracters which either subtract one value from another and vice versa or subtract one value from another and then compare the result to zero. In either case, the magnitude comparator outputs values indicating which value is greater than the other or if they are equal.
Figure 5.10 shows a basic comparator, which consists of two subtracters utilizing the negative addition discussed in the previous section. The differences are discarded, but the !borrow outputs are used to determine if the negative value is greater. If the !borrow outputs from the two
subtracters are both equal to ‘‘1’’, then it can be assumed that the two values are equal.
If one value is subtracted from the other to determine if one is lower than the other and if the value is not lower (i.e. !borrow is not zero), the result can then be compared to zero to see if the value is greater than or equal to the other. This method is probably less desirable because it tends to take longer to get a valid result and the result outputs will be valid at different times. Ideally, when multiple outputs are being produced by a circuit, they should all be available at approximately the same time (which is the advantage of the two subtracter circuit shown in Fig. 5-10 over this one).
If you are working with TTL and require a magnitude comparator, you will probably turn to the 7485, which is a four bit magnitude comparator consisting of two borrow look-ahead subtracters to ensure that the outputs are available in a minimum amount of time and are all valid at approximately the same time.
In Fig. 5-10 (as well as the multi-bit subtracter shown in the previous section), I contained related multiple bits in a single, thick line. This very common method of indicating multiple related bits is often known as a ‘‘bus’’. Other methods include using a line of a different color or style. The advantage of grouping multiple bits that function together like this should be obvious: the diagram is simpler and it is easier to see the path that related bits take.
When I use the term ‘‘related bits’’, I should point out that this does not only include the multiple bits of a binary value. You may have situations
where busses are made up of bits which are not a binary value, but perform a similar function within the circuit. For example, the memory control lines for a microprocessor are often grouped together as a bus even though each function is provided by a single bit (memory read, memory write, etc.) and they are active at different times.
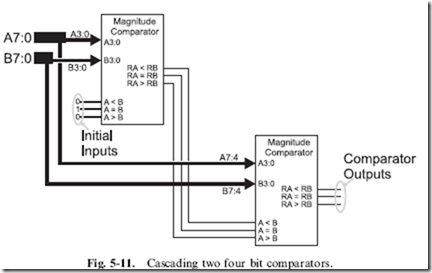
As well as indicating a complete set of related bits, a bus may be broken up into subsets, as shown in Fig. 5-11. In this diagram, I have shown how two four bit magnitude comparators can be ‘‘ganged’’ together to provide a comparison function on eight bits. The least significant four bits are passed to the first magnitude comparator and the most significant four bits are passed to the second magnitude comparator. The bits are typically listed as shown in Fig. 5-11, with the most significant bit listed first and separated from the least significant bit by a colon. In very few cases will you see the width of the bus reduced to indicate a subset of bits as I have done in Fig. 5-11; most design systems will keep the same width for a bus, even if one bit is being used in it.
Before going on, I want to make some comments about Fig. 5-11 as it provides a function that is often required when more bits must be operated on than is available by basic TTL or CMOS logic chips. To carry out the magnitude comparison operation on eight bits, I used two four bit magnitude comparator chips (modeled on the 7485) with the initial state inputs (marked ‘‘Initial Inputs’’ on Fig. 5-11) to start the chip off in the ‘‘neutral’’ state as if everything ‘‘upstream’’ (before) was equal to each other and the chip’s bits as well as any ‘‘downstream’’ (after) bits will determine which value is greater or if the two values are equal. This is a typical method for combining multiple chips to provide the capability to process more bits than one chip is able to.
Multiplication and Division
As you’ve read through this chapter, you should have noticed that there are usually many different ways of implementing different digital electronics functions. Each of the different implementation methods have their own advantages and tradeoffs – it is up to the application designer to understand what are the important ones. Nowhere is this more true than when you start discussing multiplication and division; there are a number of different methods of performing these arithmetic operations, each with their own characteristics.
Off the top of my head, I can come up with five different ways to multiply two binary numbers together. Before listing the different methods, I should make sure that I have defined the terms used in multiplication. The ‘‘multiplicand’’ is the value that is multiplied by the ‘‘multiplier’’ and typically remains static. The ‘‘multiplier’’ is the number of times that the multiplicand is added together to form the result or ‘‘product’’.
It should go without saying that if you had to multiply by a power of 2 (i.e.
1, 2, 4, 8, 16, etc.) a true multiplication operation is not required at all; the
operation can be accomplished by shifting the multiplicand. For example to
multiply a value by 4, you would simply shift the value to the left two times.
Division is the same, except the value is shifted to the right.
Understanding the basic terms ‘‘multiplier’’ and ‘‘multiplicand’’ leads to a
second method to implement a multiplication function in software – the
multiplicand is added multiplier number of times to the product. It can be
written out in ‘‘C’’ as: .
This method is painfully slow (especially for large multiplier values) and is difficult to implement in combinatorial digital logic. It is also different from the method which you were taught in school in which the multiplicand is shifted up by the radix for each digit of the multiplier. Using this method, ‘‘123’’ decimal is multiplied by ‘‘24’’ decimal in the format:
In the first line of the solution, I multiplied the multiplicand ‘‘123’’ by the least significant digit of the multiplier followed by multiplying the multiplicand by 10 (the radix) followed by the next significant digit of the multiplier. Once the multiplicand has been multiplied by each digit of the multiplier (along with the appropriate multiplication of the digit position), each product is added together to get the final result.
This method lends itself extremely well to working within binary systems. Rather than multiplying the multiplicand repeated by the radix for each digit,
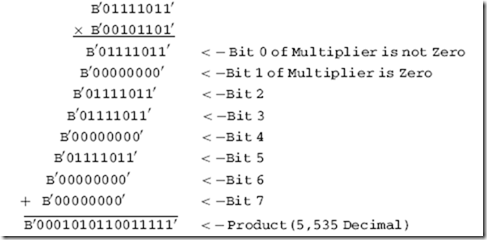
the multiplicand is simply shifted to the right (which is multiplying by two) for each bit of the multiplier. If the multiplier bit is zero, then the value added to the product is zero. The binary multiplication operation for 123 by 45 is:
This is much more efficient than the previous version in terms of execution time and not significantly more complex than the other version. The ‘‘C’’ code that implements it is:
The first version is known as ‘‘Order n’’ because it loops once for each value of the multiplier. The shift and add version shown directly above is known as ‘‘Order log2’’ because it executes the log2 of the word size of the multiplier. For the eight bit multiplication example shown here, for the first method, up to 255 loops (and addition operations) may have to be executed. For the second example, a maximum of 8 loops (one for each bit, which is a simple way to calculate log2 of a number) is required.
The final method of multiplying two numbers together is known as ‘‘Booth’s algorithm’’ and looks for opportunities to reduce the number of addition operations that are required by rounding the multiplier up and then adjusting the product by subtracting the multiplier’s zero bits that were ignored. For the example given in this section (123 multiplied by 45), Booth’s algorithm would recognize that 45, B’00101101’ rounds up to 64 (B’01000000’). Multiplying a binary number by 64 is the same as shifting left six times.
To adjust the product, the basic multiplicand (multiplied by 1) along with
all the instances where the multiplier has bit value of zero (in this case, bits one and four) have to be taken away from the rounded up value. For this example, the multiplication operation would look like:
which is the same result as we got above for a bit less work. Booth’s algorithm can produce a product in fewer, the same or more addition/subtraction operations as the previous method, so care must be taken to make sure that it is only used when it is going to provide an advantage.
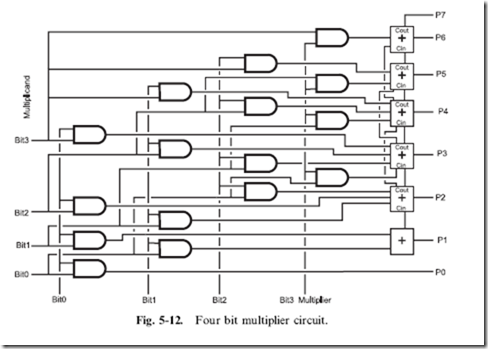
Each of the three methods presented so far requires the ability to ‘‘loop’’ through multiple iterations. This is a problem for most digital electronic circuits, as it not only requires a ‘‘clock’’ to synchronize the operations but it will also most likely take up more time than is desired. When a digital logic multiplier is designed, it typically looks something like Fig. 5-12. This circuit is wired to add all the multiplicand bits together for each possible multiplier values.
The multiplier bits are taken into account by ANDing them with each of the multiplicand bits. If a multiplier bit is zero, then the shifted up multiplicand bits are not passed to the multi-bit adders.
There are a couple points about the multi-bit adders that you should be
aware of. The first is that the maximum number of input bits for the adders used in the multiplier circuit is the number of bits in the multiplicand plus the log2 value of the multiplier. Secondly, as drawn, the adders are connected in a ‘‘ripple’’ configuration – a commercial circuit would probably wire the .
adders together as a carry look-ahead to minimize the time required for the multiplication operation to take place.
Before leaving the topic of multiplication, I should point out that all the methods presented here will handle multiplication of two’s complement negative numbers ‘‘natively’’. This is to say that no additional gates must be added to support the multiplicand or multiplier being negative.
Division is significantly more difficult to implement and is very rarely implemented in low-cost devices. Handling negative values considerably complicates the division operation and in this section, as well as most commercial solutions, negative values cannot be used for the dividend or divisor. To avoid the hardware complexities of division, software intensive solutions are normally done such as a repeated subtraction:
The bit shifting method shown for multiplication can also be used, but before comparisons can start, the divisor should be shifted up the word size of the dividend. To follow the bit shifting division code listed below you might want to do a thought experiment and single step through it with arbitrary values to see exactly how it works:
At the end of both these division algorithms, ‘‘Quotient’’ contains the quotient of the division operation and ‘‘Dividend’’ contains the remainder.
The bit shifting division algorithm could be implemented using digital
electronic gates as I demonstrated for the bit shifting multiplication algorithm, but you will find that it is quite a bit more complex than the bit shifting multiplication application in Fig. 5-12. This does not mean that there are some tricks you cannot implement if a division operation is required.
For example, if you wanted to divide a value by a known, constant value,
you could multiply it by its fraction of 256 (rather than the typical 1) and then divide by 256 (which is accomplished by shifting right by eight bits). For example, dividing 123 by 5 would be accomplished by multiplying 123 by 51 (256 divided by 5) and shifting the product (6,273) to the right by 8 bits to get the result 24. While this method seems like it’s complex, it is actually quite easy to implement in digital electronics.
Quiz
1. 6 – 5 is the same as:
(a) 6+ (-5)
(b) 5 – 6
(c) 999999
(d) B’1111 1111’
2. In a universe where infinity (the highest possible number) is one million (1,000,000); ‘‘-11’’ could be represented as:
(a) Only -11
|
(b) |
999,988 |
|
(c) |
999,989 |
|
(d) |
89 |
3. A ‘‘half adder’’:
(a) Can perform an addition operation on two bits
(b) Can add half the bits together of an addition operation
(c) Combines the ‘‘carry’’ outputs of a ‘‘full adder’’ to produce the correct result
(d) Is built from half the number of gates as a full adder
4. A ‘‘ripple adder’’ is not used in a PC or workstation processor because:
(a) Its complexity can affect the operation of other arithmetic functions
(b) The result is often wrong by one or two bits
(c) The delay required for the signal to pass through the gates can be unacceptably long
(d) It cannot handle the 32 or 64 bit addition operations required
5. B’10’ – B’01’ passed through two full subtracters produces the result:
(a) Cannot be done because a borrow operation is required
(b) B’01’ with borrow ¼ 1
(c) B’10’ with borrow ¼ 0
(d) B’01’ with borrow ¼ 0
6. Converting the four bit, two’s complement value ‘‘-4’’ to a positive number by inverting each bit and incrementing the result produces the bit pattern:
(a) B’0100’
(b) Which is five bits long and is invalid (c) B’0011’
(d) B’1100’
7. Busses are made up of:
(a) Multiple bits of a single value
(b) Multiple bits passing to the same subsystem of the application
(c) The highest speed signals in the application
(d) Related bits
8. Multiplying two four bit numbers by repeated addition:
(a) Will require up to 4 addition operations
(b) Will require up to 15 addition operations
(c) Cannot be implemented in digital electronics
(d) Is the fastest way of performing binary multiplication
9. Multiplying a binary number by 16 can be accomplished by:
(a) Clearing the least significant four bits
(b) Shifting left four bits
(c) Shifting right four bits
(d) Setting the least significant four bits
10. Dividing an eight bit value by the constant value 6 is best accomplished by:
(a) Using the repeated subtraction method
(b) Using the bit shifting method
(c) Shifting the value to the right by two and then shifting the value to the right by 1 and adding the two values.
(d) Multiplying by 256/6 (42) and shifting the product to the right
by 8 bits