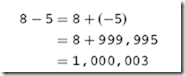Binary Arithmetic Using Digital Electronics : Adders

Binary Arithmetic Using Digital Electronics

Before going into showing how basic binary arithmetic operations are performed in digital electronic circuits, I thought it would be useful to review how you would perform basic arithmetic operations. Before discussing how many binary arithmetic operations there are, some different characteristics of binary numbers should be discussed. I realize that much of the material in this chapter introduction is a review of work that you first did in grade school, but often when confronted with situations that require you to develop binary arithmetic operations in digital electronics, this basic information can easily be forgotten and standard devices that provide this function are often overlooked.

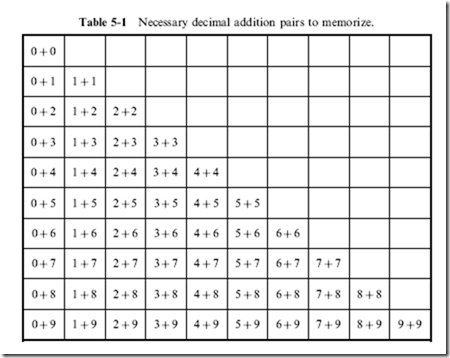
When you first learned to add decimal numbers together, you probably were required to memorize all 100 different combinations of single digit parameters when only 55 are really required. In Table 5-1, I have listed the 55 pairs which have to be memorized; the remaining 45 pairs do not have to be memorized because of the commutative law which states:

A + B =B + A

and means that the number pairs like ‘‘4+7’’ and ‘‘7+ 4’’ are equivalent.

The result of adding each of these two parameters produces either a single digit or double digit sum. The double digit sum indicates that the value of the result is greater than could be represented in a single digit of the number base. For decimal numbers, the maximum value that can be represented by a single digit is ‘‘9’’. Looking at the general case, the maximum value that can be represented by a number system is the base minus one. So, for the binary number system (base 2), the maximum value is ‘‘1’’; for hexadecimal (base 16), the maximum value is ‘‘15’’ (or ‘‘0x0F’’).

The leftmost digit of a double digit number is known as the ‘‘carry’’ digit.

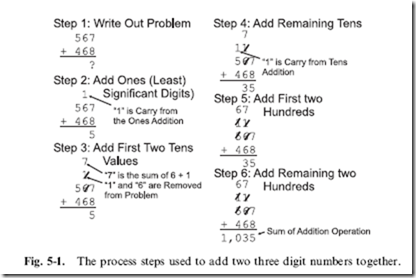
In Chapter 4, I showed how multi-digit numbers are made up of single digit values multiplied by powers of their base. Knowing the sums of the 55 addition pairs of Table 5-1, multi-digit numbers can be added together

by working through pairs of numbers, as I show in Fig. 5-1. This is a rather pedantic way of showing addition and I’m sure that when you add two multi- digit numbers together, you are much more efficient, but when you were learning, this was probably the process that you went through.

While saying that you are much more efficient, it really comes down to the idea that you are able to recognize that one plus another number is the same as incrementing the other number. You are still only adding one digit at a time and the carry is ‘‘rippling’’ to the next significant digit. Carry ‘‘ripple’’ is an important concept that will be discussed in more detail in the next section.

Subtraction has many of the same issues as addition, but with some additional complexities. The first being that you cannot simplify your memorization of the 100 pairs of subtracted parameters as you did for addition; the commutative law does not apply to subtraction as it did for addition. For example,

Next, if the number being taken away is greater than the original number, the result (or ‘‘difference’’) could be less than 0 or ‘‘negative’’. There is a very big question on how to represent that negative number. Typically, it is represented as a value with a ‘‘minus’’ or ‘‘subtraction’’ sign in front of it, e.g. ‘‘-2’’.

The minus sign is only used when the digit cannot ‘‘borrow’’ from the next significant digit, as shown in Fig. 5-2. The result of 25 minus 9 is 16, with the ones borrowing 10 from the tens column (the next significant digit) to allow the operation to proceed without a negative result.

Subtraction can also be expressed as adding a negative value and can be written out as:

This should not be a surprise to you unless you consider the following philosophical question: What would happen if infinity was arbitrarily defined as one million (1,000,000)? Instead of adding a minus sign to our value to make it negative, we could subtract it from ‘‘infinity’’.

For example, if we had the problem:

we could define ‘‘-5’’ as one million subtract 5 or ‘‘999,995’’. Now, going back to the addition of the negative number and substituting in ‘‘999,995’’ for ‘‘-5’’ we get:

Since a million is defined as infinity and has no meaning, it can be taken away from the result, leaving us with the difference of 8 minus 5 being ‘‘3’’. This method may seem to be overly complex, but I will show you how this applies to digital electronics later in the chapter.

Like addition, the method presented here for subtraction is carried out a single digit at a time with the need to borrow from the next more significant digit being similar to passing the carry digit in addition. Like the ‘‘ripple carry’’ in addition, the ‘‘borrow’’ in subtraction can also be thought of as a ‘‘ripple’’ operation.

Multiplication and division have, not surprisingly, many of the same issues and when I discuss them later in this chapter, I will review them with you. Before reading the section discussing multiplication and division, I suggest that you review these operations and try to think of how they can be accomplished using digital electronics.

Adders

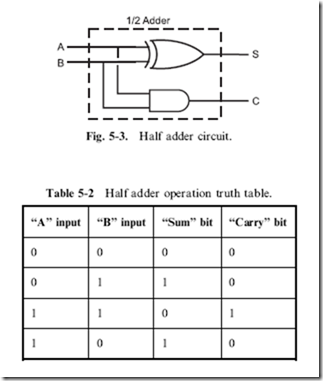
The circuit shown in Fig. 5-3 will add two bits together and output the sum (‘‘S’’) bit along with a carry (‘‘C’’) bit, if both inputs are ‘‘1’’ and the sum is ‘‘2’’, which is greater than the maximum number that can be represented by the number base (which is 1 for binary). Table 5-2 is a truth table, showing the output of each bit for different input values. You should be able to see that the ‘‘sum’’ bit is 1 when one or the other (but not both) of the two input bits is 1 and the ‘‘carry’’ bit is 1 only when both input bits are 1.

The adder is the first practical use most people have for the XOR gate and its function can be seen very clearly in Table 5-2 for the sum bit. Along with the XOR gate providing the function for the sum bit, you should also recognize that the carry bit is the output of a simple AND gate.

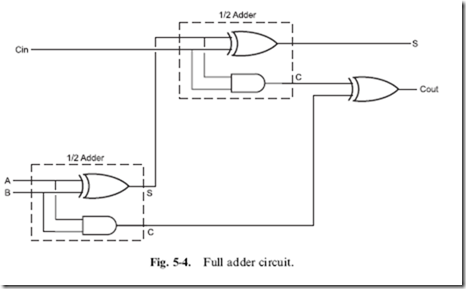
This simple digital electronic circuit is known as a ‘‘half adder’’ because it will handle half the operations required of the general case addition circuit. The ‘‘full adder’’ (Fig. 5-4) starts with a half adder and adds another bit (which is the less significant bit’s ‘‘carry’’ output) to its sum. Put another way, the full adder adds three individual bits together (two bits being the digit inputs and the third bit assumed to be carry from the addition of the next least-significant bit addition operation, known as ‘‘Cin’’).

You can analyze the operation of the full adder to check on its operation.

The sum bit is 1 only if one or three of the input bits is 1. In the half adder, I showed that the sum bit could be written out as:

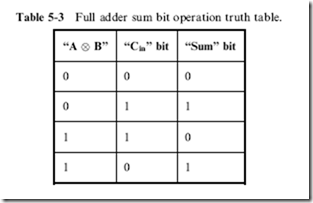
and should only be ‘‘1’’ if only one of the two inputs was 1. To understand the logic required to produce the sum bit for the three bit full adder, I created Table 5-3 in which the XOR output of the A and B inputs was given a single column entry. From the data presented in this table, you can see that the sum could be expressed as:

which, if you look back at Fig. 5-4, is exactly how it is implemented in the ‘‘full adder’’.

The carry output bit is 1 if two or three of the input bits are 1. As an

exercise, you may wish to create a truth table and reduce it down to see if you can match the carry gate logic of Fig. 5-3, but you can write out and reduce a sum of products equation quite easily:

which is exactly the carry logic circuit shown in Fig. 5-2. This type of analysis is useful to do when you are trying to puzzle out what a circuit is doing or to confirm that it is doing exactly what you expect it to do. It is also good practice of using the logic equation optimization skills first presented in Chapter 2.

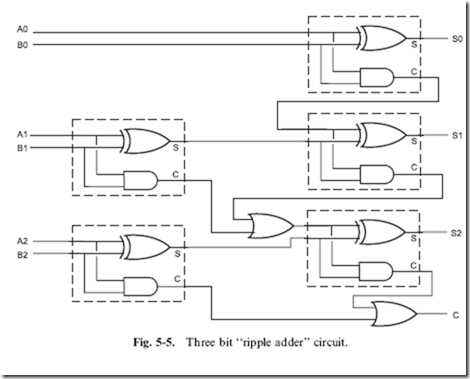
Multiple full adders can be chained together (like in Fig. 5-5) to produce a multi-bit adder in which the carry results for each bit ‘‘ripples’’ through the various adder circuits. For most applications, this ‘‘ripple carry adder’’ can be used safely, but in something like your PC’s processor, where quite a few bits are required and the adder is expected to execute quickly, the time required for the carry to ripple through the adders is prohibitive.

The solution to this problem is the ‘‘carry look-ahead’’ adder in which each bit takes not only the appropriate bits for input but also all the least

significant bits that can affect the bit. The length of time the carry look-ahead adder needs to produce a sum is generally independent of the number of bits in the operation (unlike the time the ripple adder requires to produce a sum which is a function of the number of bits). Table 5-4 lists the different inputs and expected outputs for a three bit carry look-ahead adder. Reducing the

Table 5-4 Carry look-ahead adder input/output truth table.

Table 5-4 Continued.

Table 5-4 Continued.

information from this table, I have listed the equations for the three sum bits and the carry bit below:

It was a major effort on my part to reduce the equations for each sum bit and the carry bit. To do this, I used the truth table reduction method discussed in Chapter 2. To reduce the number of terms in the resulting sum of products equations, I first deleted all the instances where the specific bit was not ‘‘1’’ – in every case, this reduced the number of instances by half. Next, I worked at combining instances that were similar and found that rather than combining ‘‘don’t care’’ bits, I found a number of places where two bits were XORed together. In the resulting equations, I kept the ‘‘XOR’’ terms in, even though when the ‘‘technology optimization’’ stage of the development effort is completed, these gates will be reduced to the technology’s basic gates.

If you read through the equations and try to understand them, you will find that they do make a kind of sense. Obviously, as more bits are added to the carry look-ahead adder, the circuit becomes much more complex. Despite this complexity, the carry look-ahead is the most efficient way to provide an adder circuit for large bit words in fast applications.