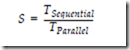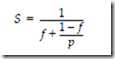Parallel Architecture
One method of improving the performance of a processor is to decrease the time needed to execute instructions. This will work up to a limit of about 400 MHz (Stone, 1991), at which point an effect known as ringing on busses prohibits further speedup with conventional bus technology. This is not to say that higher clock speeds are not possible, because indeed current microprocessors have clock rates well above 400 MHz, but that “shared bus” approaches become impractical at these speeds. As conventional architectural approaches to improving performance wear thin, we need to consider alternative methods of improving performance.
One alternative approach to increasing bus speed is to increase the number of processors, and decompose and distribute a single program onto the processors. This approach is known as parallel processing, in which a number of processors work collectively, in parallel, on a common problem. We see an example of parallel processing earlier in the chapter with pipelining. For that case, four processors are connected in series (Figure 10-3), each performing a different task, like an assembly line in a factory. The interleaved memory described in Chapter 7 is another example of pipelining.
A parallel architecture can be characterized in terms of three parameters: (1) the number of processing elements (PEs); (2) the interconnection network among the PEs; and (3) the organization of the memory. In the four-stage instruction pipeline of Figure 10-3, there are four PEs. The interconnection network among the PEs is a simple ring. The memory is an ordinary RAM that is external to the pipeline.
Characterizing the architecture of a parallel processor is a relatively easy task, but measuring the performance is not nearly so simple. Although we can easily mea- sure the increased speed that a simple enhancement like a pipeline offers, the overall speedup is data dependent: not all programs and data sets map well onto a pipelined architecture. Other performance considerations of pipelined architectures that are also data dependent are the cost of flushing a pipeline, the increased area cost, the latency (input to output delay) of the pipeline, etc.
A few common measures of performance are parallel time, speedup, efficiency, and throughput. The parallel time is simply the absolute time needed for a pro- gram to execute on a parallel processor. The speedup is the ratio of the time for a program to execute on a sequential (non-parallel, that is) processor to the time for that same program to execute on a parallel processor. In a simple form, we can represent speedup (S, now in the context of parallel processing) as:
Since a sequential algorithm and a parallel version of the same algorithm may be programmed very differently for each machine, we need to qualify TSequential and TParallel so that they apply to the best implementation for each machine.
There is more to the story. If we want to achieve a speedup of 100, it is not enough to simply distribute a single program over 100 processors. The problem is that not many computations are easily decomposed in a way that fully utilizes the available PEs. If there are even a small number of sequential operations in a parallel program, then the speedup can be significantly limited. This is summarized by Amdahl’s law, in which speedup is expressed in terms of the number of processors p and the fraction of operations that must be performed sequentially f:
For example, if f = 10% of the operations must be performed sequentially, then speedup can be no greater than 10 regardless of how many processors are used:
This brings us to measurements of efficiency. Efficiency is the ratio of speedup to the number of processors used. For a speedup of 5.3 with 10 processors, the efficiency is:
If we double the number of processors to 20, then the speedup increases to 6.9 but the efficiency reduces to 34%. Thus, parallelizing an algorithm can improve performance to a limit that is determined by the amount of sequential operations. Efficiency is drastically reduced as speedup approaches its limit, and so it does not make sense to simply use more processors in a computation in the hope that a corresponding gain in performance will be achieved.
Throughput is a measure of how much computation is achieved over time, and is of special concern for I/O bound and pipelined applications. For the case of a four stage pipeline that remains filled, in which each pipeline stage completes its task in 10 ns, the average time to complete an operation is 10 ns even though it takes 40 ns to execute any one operation. The overall throughput for this situation is then:
THE FLYNN TAXONOMY
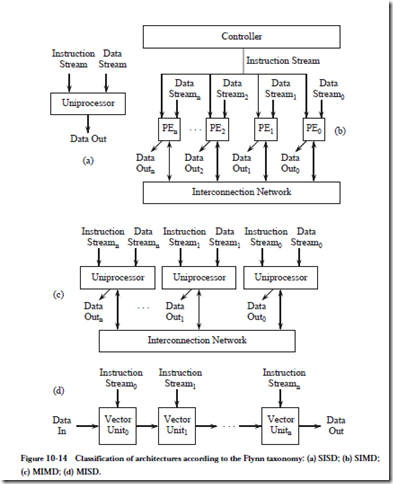
Computer architectures can be classified in terms of their instruction streams and their data streams, using a taxonomy developed by M. J. Flynn (Flynn, 1972). A conventional sequential processor fits into the single-instruction stream, single data stream (SISD) category, as illustrated in Figure 10-14a. Only a single instruction is executed at a time in a SISD processor, although pipelining may allow several instructions to be in different phases of execution at any given time.
In a single instruction stream, multiple data stream (SIMD) processor, several identical processors perform the same sequence of operations on different data sets, as illustrated in Figure 10-14b. A SIMD system can be thought of as a room filled with mail sorters, all sorting different pieces of mail into the same set of bins.
In a multiple instruction stream, multiple data stream (MIMD) processor, several processors perform different operations on different data sets, but are all coordinated to execute a single parallel program, as illustrated in Figure 10-14c. An example of a MIMD processor is the Sega home video entertainment system, which has four processors for (1) sound synthesis (a Yamaha synthesis processor); (2) sound filtering (a Texas Instruments programmable sound generator); (3) program execution (a 68000); and (4) background processing (a Z80). We will see more of the Sega Genesis in a Case Study at the end of the chapter.
In a multiple instruction stream, single data stream (MISD) processor, a single data stream is operated on by several functional units, as illustrated in Figure 10-14d. The data stream is typically a vector of several related streams. This con- figuration is known as a systolic array, which we see in Chapter 3 in the form of an array multiplier.
INTERCONNECTION NETWORKS
When a computation is distributed over a number of PEs, the PEs need to communicate with each other through an interconnection network. There is a host of topologies for interconnection networks, each with their own characteristics in terms of crosspoint complexity (an asymptotic measure of area), diameter (the length of the worst case path through the network), and blocking (whether or not a new connection can be established in the presence of other connections). A few representative topologies and control strategies for configuring networks are described below.
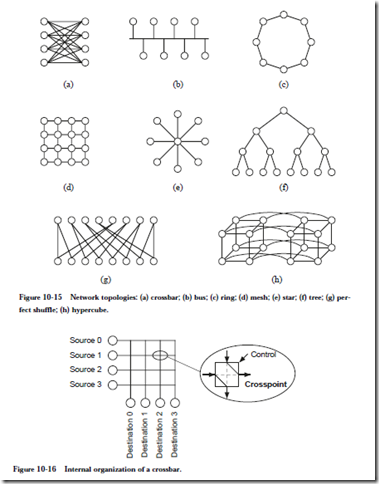
One of the most powerful network topologies is the crossbar, in which every PE is directly connected to every other PE. An abstract view of a crossbar is illustrated in Figure 10-15a, in which four PEs are interconnected. In a closeup view illustrated in Figure 10-16, the crossbar contains crosspoint switches, which are configurable devices that either connect or disconnect the lines that go through it. In general, for N PEs, the crosspoint complexity (the number of crosspoint switches) is N2. In Figure 10-15a, N = 4 (not 8) because the output ports of the PEs on the left and the input ports of the PEs on the right belong to the same PEs. The crosspoint complexity is thus 42 = 16. The network diameter is 1 since every PE can directly communicate with every other PE, with no intervening PEs. The number of crosspoint switches that are traversed is not normally considered in evaluating the network diameter. The crossbar is strictly nonblocking, which means that there is always an available path between every input and output regardless of the configuration of existing paths.
At the other extreme of complexity is the bus topology, which is illustrated in Figure 10-15b. With the bus topology, a fixed amount of bus bandwidth is shared among the PEs. The crosspoint complexity is N for N PEs, and the net- work diameter is 1, so the bus grows more gracefully than the crossbar. There can only be one source at a time, and there is normally only one receiver, so blocking is a frequent situation for a bus.
In a ring topology, there are N crosspoints for N PEs as shown in Figure 10-15c. As for the crossbar, each crosspoint is contained within a PE. The network diameter is N/2, but the collective bandwidth is N times greater than for the case of the bus. This is because adjacent PEs can communicate directly with each other over their common link without affecting the rest of the network.
In the mesh topology, there are N crosspoints for N PEs, but the diameter is only 2 N as shown in Figure 10-15d. All PEs can simultaneously communicate in just 3 N steps, as discussed in (Leighton, 1992) using an off-line routing algorithm (in which the crosspoint settings are determined external to the PEs).
In the star topology, there is a central hub through which all PEs communicate as shown in Figure 10-15e. Since all of the connection complexity is centralized, the star can only grow to sizes that are bounded by the technology, which is normally less than for decentralized topologies like the mesh. The crosspoint complexity within the hub varies according to the implementation, which can be anything from a bus to a crossbar.
In the tree topology, there are N crosspoints for N PEs, and the diameter is 2log2N – 1 as shown in Figure 10-15f. The tree is effective for applications in which there is a great deal of distributing and collecting of data.
In the perfect shuffle topology, there are N crosspoints for N PEs as shown in Figure 10-15g. The diameter is log2N since it takes log2N passes through the net- work to connect any PE with any other in the worst case. The perfect shuffle name comes from the property that if a deck of 2N cards, in which N is an integer, is cut in half and interleaved N times, then the original configuration of the deck is restored. All N PEs can simultaneously communicate in 3log2N – 1 passes through the network as presented in (Wu and Feng, 1981).
Finally, the hypercube has N crosspoints for N PEs, with a diameter of log2N-1, as shown in Figure 10-15h. The smaller number of crosspoints with respect to the perfect shuffle topology is balanced by a greater connection complexity in the PEs.
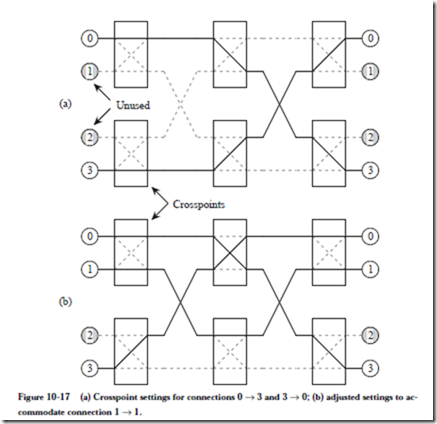
Let us now consider the behavior of blocking in interconnection networks. Figure 10-17a shows a configuration in which four processors are interconnected
with a two-stage perfect shuffle network in which each crosspoint either passes both inputs straight through to the outputs, or exchanges the inputs to the out- puts. A path is enabled from processor 0 to processor 3, and another path is enabled from processor 3 to processor 0. Neither processor 1 nor processor 2 needs to communicate, but they participate in some arbitrary connections as a side effect of the crosspoint settings that are already specified.
Suppose that we want to add another connection, from processor 1 to processor
1. There is no way to adjust the unused crosspoints to accommodate this new connection because all of the crosspoints are already set, and the needed connection does not occur as a side effect of the current settings. Thus, connection 1 ® 1 is now blocked.
If we are allowed to disturb the settings of the crosspoints that are currently in use, then we can accommodate all three connections, as illustrated in Figure 10-17b. An interconnection network that operates in this manner is referred to as a rearrangeably nonblocking network.
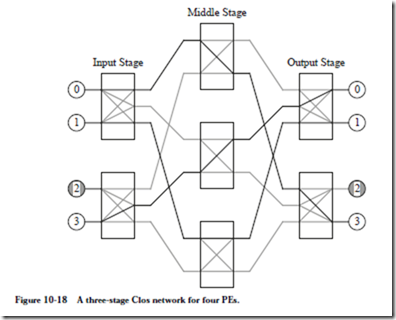
The three-stage Clos network is strictly nonblocking. That is, there is no need to disturb the existing settings of the crosspoints in order to add another connection. An example of a three stage Clos network is shown in Figure 10-18 for four
PEs. In the input stage, each crosspoint is actually a crossbar that can make any connection of the two inputs to the three outputs. The crosspoints in the middle stage and the output stage are also small crossbars. The number of inputs to each input crosspoint and the number of outputs from each output crosspoint is selected according to the desired complexity of the crosspoints, and the desired complexity of the middle stage.
The middle stage has three crosspoints in this example, and in general, there are (n – 1) + (p – 1) + 1 = n + p – 1 crosspoints in the middle stage, in which n is the number of inputs to each input crosspoint and p is the number of outputs from each output crosspoint. This is how the three-stage Clos network maintains a strictly nonblocking property. There are n – 1 ways that an input can be blocked
at the output of an input stage crosspoint as a result of existing connections. Similarly, there are p – 1 ways that existing connections can block a desired connection into an output crosspoint. In order to ensure that every desired connection can be made between available input and output ports, there must be one more path available.
For this case, n = 2 and p = 2, and so we need n + p – 1 = 2 + 2 – 1 = 3 paths from every input crosspoint to every output crosspoint. Architecturally, this relationship is satisfied with three crosspoints in the middle stage that each connect every input crosspoint to every output crosspoint.
EXAMPLE: STRICTLY NONBLOCKING NETWORK
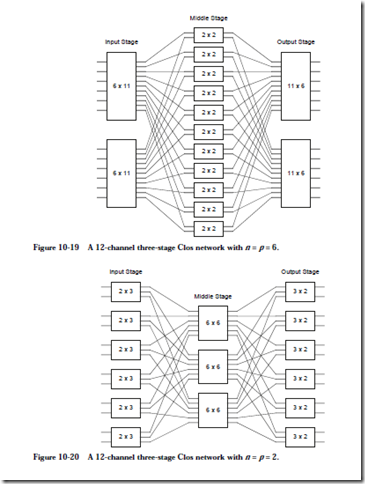
For this example, we want to design a strictly nonblocking (three-stage Clos) network for l2 channels (l2 inputs and l2 outputs to the network) while maintaining a low maximum complexity of any crosspoint in the network.
There are a number of ways that we can organize the network. For the input stage, we can have two input nodes with 6 inputs per node, or 6 input nodes with two inputs per node, to list just two possibilities. We have similar choices for the output stage. Let us start by looking at a configuration that has two nodes in the input stage, and two nodes in the output stage, with 6 inputs for each node in the input stage and 6 outputs for each node in the output stage. For this case, n = p = 6, which means that n + p – l = ll nodes are needed in the mid- dle stage, as shown in Figure lO-l9. The maximum complexity of any node for this case is 6 ´ ll = 66, for each of the input and output nodes.
Now let us try using 6 input nodes and 6 output nodes, with two inputs for each input node and two outputs for each output node. For this case, n = p = 2, which means that n + p – l = 3 nodes are needed in the middle stage, as shown in Figure lO-2O. The maximum node complexity for this case is 6 ´ 6 = 36 for each of the middle stage nodes, which is better than the maximum node complexity of 66 for the previous case.
Similarly, networks for n = p = 4 and n = p = 3 are shown in Figure lO-2l and Figure lO-22, respectively. The maximum node complexity for each of these net- works is 4 ´ 7 = 28 and 4 ´ 4 = l6, respectively. Among the four configurations studied here, n = p = 3 gives the lowest maximum node complexity.