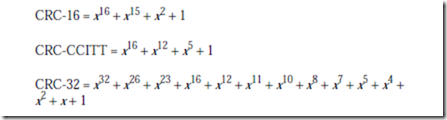9.4 Communication Errors and Error Correcting Codes
In situations involving communications between computers, and even inside of a computer system, there is a finite chance that the data is received in error, due to noise in the communication channel. The data representations we have considered up to this point make use of the binary symbols 1 and 0. In reality, the binary symbols take on physical forms such as voltages or electric current. The physical form is subject to noise that is introduced from the environment, such as atmospheric phenomena, gamma rays, and power fluctuations, to name just a few. The noise can cause errors, also known as faults, in which a 0 is turned into a 1 or a 1 is turned into a 0.
Suppose that the ASCII character ‘b’ is transmitted from a sender to a receiver, and during transmission, an error occurs, so that the least significant bit is inverted. The correct bit pattern for ASCII ‘b’ is 1100010. The bit pattern that the receiver sees is 1100011, which corresponds to the character ‘c.’ There is no way for the receiver to know that an error occurred simply by looking at the received character. The problem is that all of the possible 27 ASCII bit patterns represent valid characters, and if any of the bit patterns is transformed into another through an error, then the resulting bit pattern appears to be valid.
It is possible for the sender to transmit additional “check bits” along with the data bits. The receiver can examine these check bits and under certain conditions not only detect errors, but correct them as well. Two methods of computing these additional bits are described below. We start by introducing some preliminary information and definitions.
9.4.1 BIT ERROR RATE DEFINED
There are many different ways that errors can be introduced into a system, and those errors can take many different forms. For the moment, we will assume that the probability that a given bit is received in error is independent of the probability that other bits near it are received in error. In this case, we can define the bit error rate (BER) as the probability that a given bit is erroneous. Obviously this must be a small number, and is usually less than 10-12 errors per bit examined for fiber networks. That means, loosely speaking, that as bits are examined, only one in every 1012 bits will be erroneous (in radio networks, as many as 1 in every 100 packets may contain an error.)
Inside of a computer system typical BER’s may run 10-18 or less. As a rough estimate, if the clock rate of the computer is 500 MHz, and 32 bits are manipulated during each clock period, then the number of errors per second for that portion of the computer will be 10-18 ´ 100 ´ 106 ´ 32 or 1.6 ´ 10-9 errors per second, approximately one erroneous bit once every 5 years.
On the other hand, if one is receiving a bit stream from a serial communications line at, say, 1 million bits per second, and the BER is 10-10, then the number of errors per second will be 1 ´ 106 ´ 10-10 or 10-4 errors per second, approximately 10 errors per day.
9.4.2 ERROR DETECTION AND CORRECTION
One of the simplest and oldest methods of error detection was used to detect errors in transmitting and receiving characters in telegraphy. A parity bit, 1 or 0, was added to each character to make the total number of 1’s in the character even or odd, as agreed upon by sender and receiver. In our example of transmitting the ASCII character ‘b,’ 1100010, assuming even parity, a 1 would be attached as a parity bit to make the total number of 1’s even, resulting in the bit pattern 11000101 being transmitted. The receiver could then examine the bit pattern, and if there was an even number of 1’s, the receiver could assume that the character was received without error. (This method fails if there is a significant probability of two or more bits being received in error. In this case, other methods must be used, as discussed later in this section.) The intuition behind this approach is explored below.
Hamming Codes
If additional bits are added to the data then it is possible to not only detect errors, but to correct them as well. Some of the most popular error-correcting codes are based on the work of Richard Hamming while at Bell Telephone Labo- ratories (now Lucent Technologies).
We can detect single-bit errors in the ASCII code by adding a redundant bit to each codeword (character). The Hamming distance defines the logical distance between two valid codewords, as measured by the number of digits that differ between the codewords. If a single bit changes in an ASCII character, then the resulting bit pattern represents a different ASCII character. The corresponding Hamming distance for this code is 1. If we recode the ASCII table so that there is a Hamming distance of 2 between valid codewords, then two bits must change in order to convert one character into another. We can then detect a single-bit error because the corrupted word will lie between valid codewords.
One way to recode ASCII for a Hamming distance of two is to assign a parity bit, which takes on a value of 0 or 1 to make the total number of 1’s in a code- word odd or even. If we use even parity, then the parity bit for the character ‘a’ is 1 since there are three 1’s in the bit pattern for ‘a’: 1100001 and assigning a parity bit of 1 (to the left of the codeword here) makes the total number of 1’s in the recoded ‘a’ even: 11100001. This is illustrated in Figure 9-8. Similarly, the parity
bit for ‘c’ is 0 which results in the recoded bit pattern: 01100011. If we use odd parity instead, then the parity bits take on the opposite values: 0 for ‘a’ and 1 for ‘c,’ which results in the recoded bit patterns 01100001 and 11100011, respectively.
The recoded ASCII table now has 28 = 256 entries, of which half of the entries (the ones with an odd number of 1’s) represent invalid codewords. If an invalid codeword is received, then the receiver knows that an error occurred and can request a retransmission.
A retransmission may not always be practical, and for these cases it would be helpful to both detect and correct an error. The use of a parity bit will detect an error, but will not locate the position of an error. If the bit pattern 11100011 is received in a system that uses even parity, then the presence of an error is known because the parity of the received word is odd. There is not enough information from the parity bit alone to determine if the original pattern was ‘a’, ‘b’, or any of five other characters in the ASCII table. In fact, the original character might even be ‘c’ if the parity bit itself is in error.
In order to construct an error correcting code that is capable of detecting and correcting single-bit errors, we must add more redundancy than a single parity bit provides to the ASCII code by further extending the number of bits in each codeword. For instance, consider the bit pattern for ‘a’: 1100001. If we wish to detect and correct a single bit error in any position of the word, then we need to assign seven additional bit patterns to ‘a’ in which exactly one bit changes in the original ‘a’ codeword: 0100001, 1000001, 1110001, 1101001, 1100101, 1100011, and 1100000. We can do the same for ‘b’ and the remaining characters, but we must construct the code in such a way that no bit pattern is common to more than one ASCII character, otherwise we will have no means to unambig- uously determine the original bit pattern.
A problem with using redundancy in this way is that we assign eight bit patterns to every character: one for the original bit pattern, and seven for the neighboring error patterns. Since there are 27 characters in the ASCII code, and since we need 23 bit patterns for every character, then we can only recode 27/23 = 24 characters if we use only the original seven bits in the representation.
In order to recode all of the characters, we must add additional redundant bits (also referred to as check bits) to the codewords. Let us now determine how many bits we need. If we start with a k-bit word that we would like to recode, and we use r check bits, then the following relationship must hold:
The reasoning behind this relationship is that for each of the 2k original words, there are k bit patterns in which a single bit is corrupted in the original word, plus r bit patterns in which one of the check bits is in error, plus the original uncorrupted bit pattern. Thus, our error correcting code will have a total of 2k ´ (k + r + 1) bit patterns. In order to support all of these bit patterns, there must be enough bit patterns generated by k + r bits, thus 2k+r must be greater than or equal to the number of bit patterns in the error correcting code. There are k = 7 bits in the ASCII code, and so we must now solve for r. If we try a few successive values, starting at 1, we find that r = 4 is the smallest value that satisfies relation 8.1. The resulting codewords will thus have 7 + 4 = 11 bits.
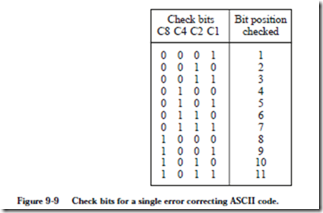
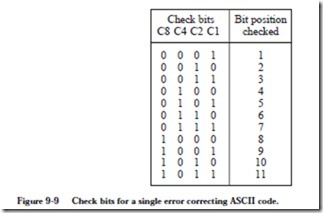
We now consider how to recode the ASCII table into the 11-bit code. Our goal is to assign the redundant bits to the original words in such a way that any single-bit error can be identified. One way to make the assignment is shown in Figure 9-9. Each of the 11 bits in the recoded word are assigned a position in the
table indexed from 1 to 11, and the 4-bit binary representations of the integers 1 through 11 are shown next to each index. With this assignment, reading across each of the 11 rows of four check bits, there is a unique positioning of the 1 bits in each row, and so no two rows are the same. For example, the top row has a single 1 in position C1, but no other row has only a single 1 in position C1 (other rows have a 1 in position C1, but they also have 1’s in the other check bit positions.)
Now, reading down each of the four check bit columns, the positions of the 1 bits tell us which bits, listed in the rightmost ‘Bit position checked’ column, are included in a group that must form even parity. For example, check bit C8 covers a group of 4 bits in positions 8, 9, 10, and 11, that collectively must form even parity. If this property is satisfied when the 11-bit word is transmitted, but an error in transmission causes this group of bits to have odd parity at the receiver, then the receiver will know that there must be an error in either position 8, 9, 10, or 11. The exact position can be determined by observing the remaining check bits, as we will see.
In more detail, each bit in the 11-bit encoded word, which includes the check bits, is assigned to a unique combination of the four check bits C1, C2, C4, and C8. The combinations are computed as the binary representation of the position of the bit being checked, starting at position 1. C1 is thus in bit position 1, C2 is in position 2, C4 is in position 4, etc. The check bits can appear anywhere in the word, but normally appear in positions that correspond to powers of 2 in order to simplify the process of locating an error. This particular code is known as a single error correcting (SEC) code.
Since the positions of the 1’s in each of the check bit combinations is unique, we can locate an error by simply observing which of the check bits are in error. Con- sider the format shown in Figure 9-10 for the ASCII character ‘a’. The values of
the check bits are determined according to the table shown in Figure 9-9. Check bit C1 = 0 creates even parity for the bit group {1, 3, 5, 7, 9, 11}. The members in this group are taken from the positions that have 1’s in the C1 column in Figure 9-9. Check bit C2 = 1 creates even parity for the bit group {2, 3, 6, 7, 10, 11}. Similarly, check bit C4 = 0 creates even parity for the bit group {4, 5, 6, 7}. Finally, check bit C8 = 0 creates even parity for the bit group {8, 9, 10, 11}.
As an alternative to looking up members of a parity group in a table, in general, bit n of the coded word is checked by those check bits in positions b1, b2, …, bj such that b1 + b2 + … + bj = n. For example, bit 7 is checked by bits in positions 1, 2, and 4 because 1 + 2 + 4 = 7.
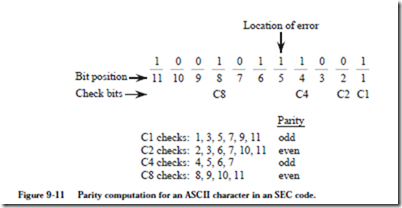
Now suppose that a receiver sees the bit pattern 10010111001. Assuming that the SEC code for ASCII characters described above is used, what character was sent? We start by computing the parity for each of the check bits as shown in Figure 9-11. As shown in the figure, check bits C1 and C4 have odd parity. In order to locate the error, we simply add up the positions of the odd check bits. The error then, is in position 1 + 4 = 5. The word that was sent is 10010101001. If we strip away the check bits, then we end up with the bit pattern 1000100 which corresponds to the ASCII character ‘D’.
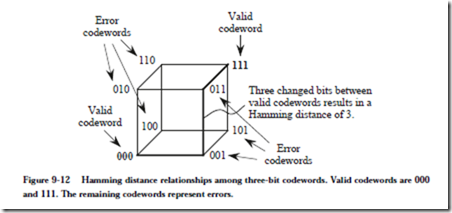
One way to think about an SEC code is that valid codewords are spaced far enough apart so that a single error places a corrupted codeword closer to one particular valid codeword than to any other valid codeword. For example, consider an SEC code for a set of just two symbols: {000, 111}. The Hamming distance relationships for all three-bit patterns are shown for this code in the cube in Figure 9-12. The cube has correspondingly higher dimensions for larger word sizes,
resulting in what is called a hypercube. The two valid codewords are shown on opposing vertices. Any single bit error will locate an invalid codeword at a different vertex on the cube. Every error codeword has a closest valid codeword, which makes single error correction possible.
SECDED Encoding
If we now consider the case in which there are two errors, then we can see that the SEC code works for double error detection (DED), but not for double error correction (DEC). This is sometimes referred to as SECDED encoding. Since valid codewords are spaced at a Hamming distance of 3, two errors will locate an error codeword on the cube, and thus two errors can be detected. The original codeword cannot be determined unambiguously, however, since vertices that correspond to two errors from one codeword overlap vertices that corre- spond to a single error from another codeword. Thus, every SEC code is also a DED code, but every DED code is not necessarily a DEC code. In order to correct two errors, a Hamming distance of five must be maintained. In general, a Hamming distance of p + 1 must be maintained in order to detect p errors, and a Hamming distance of 2p + 1 must be maintained to correct p errors.
9.4.3 VERTICAL REDUNDANCY CHECKING
The SEC code described in the previous section is used for detecting and correcting single bit errors in individual data words. Redundant bits are added to each data word, and each resulting codeword is treated independently. The recoding scheme is sometimes referred to as horizontal or longitudinal redundancy checking (LRC) because the width of the codeword is extended for the redundant bits.
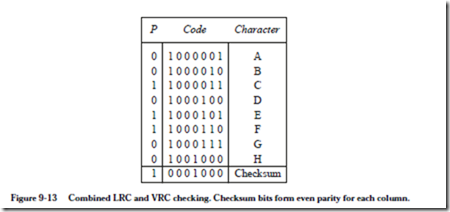
An alternative approach is to use a vertical redundancy checking (VRC) code, in which a checksum word is added at the end of a group of words that are trans- mitted. In this case, parity is computed on a column by column basis, forming a checksum word that is appended to the message. The checksum word is computed and transmitted by the sender, and is recomputed and compared to the transmitted checksum word by the receiver. If an error is detected, then the receiver must request a retransmission since there is not enough redundancy to identify the position of an error. The VRC and LRC codes can be combined to improve error checking, as shown for the ASCII characters ‘A’ through ‘H’ in Figure 9-13.
In some situations, errors are bursty, and may corrupt several contiguous bits both horizontally and vertically. A more powerful scheme such as cyclic redundancy checking (CRC) is more appropriate for this situation, which is a variation of VRC checking in which the bits are grouped in a special way, as described in the next section.
9.4.4 CYCLIC REDUNDANCY CHECKING
Cyclic redundancy checking (CRC) is a more powerful error detection and correction scheme that operates in the presence of burst errors, which each begin and end with a bit error, with zero or more intervening corrupted bits. The two endpoint corrupted bits are included in the burst error. If the length of a burst error is B, then there must be B or more uncorrupted bits between burst errors.
CRCs use polynomial codes, in which a frame to be transmitted is divided by a polynomial, and the remainder is appended to the frame as a frame check sequence (FCS), commonly known as the CRC digits. The frame is transmitted (or stored) along with the CRC digits. After receiving the frame, the receiver then goes through the same computation, using the same polynomial, and if the remainders agree then there are no detectable errors. There can be undetectable errors, and the goal in creating a CRC code is to select a polynomial that covers the statistically likely errors for a given fault model.
The basic approach starts with a k-bit message to be transmitted, M(x), which is appended with n 0’s in which n is the degree of the generator polynomial, G(x), with k > n. This extended form of M(x) is divided by G(x) using modulo 2 arithmetic (in which carries and borrows are discarded), and then the remainder, R(x), which is no more than n bits wide, forms the CRC digits for M(x).
As an example, consider a frame to be transmitted:
(10011) is divided into the dividend, but the magnitudes of the divisor and dividend do not play a role in determining whether the divisor “goes into” the dividend at the location of a particular digit. All that matters is that the number of bits in the divisor (which has no leading zeros) matches the same number of bits in the dividend (which also must not have leading zeros at the position being checked.) Note that there are no borrows in modulo-2 subtraction, and that a bit-by-bit exclusive-OR (XOR) operation between the divisor and the dividend achieves the same result.
Now suppose that the transmitted frame T(x) = M(x) + R(x) gets corrupted during transmission. The receiver needs to detect that this has happened. The receiver divides the received frame by G(x), and all burst errors that do not include G(x) as a factor will be caught because there will be a nonzero remainder for these cases. That is, as long as the 1’s in 10011 do not coincide with the positions of errors in the received frame, all errors will be caught. In general, a polynomial code of degree n will catch all burst errors of length < n.
Common polynomials that give good error coverage include:
A deeper analysis of CRC codes is beyond the scope of this book, and the reader is referred to (Hamming, 1986) for further details.
EXAMPLE: DOUBLE ERROR CORRECTION
Consider how many check bits are needed for a double-error correcting ASCII code. There are k = 7 bits for each ASCII character, and we need to add r check bits to each codeword. For each of the 2k ASCII characters there are k + r possible one-bit error patterns, there are![]() possible two-bit error pat-terns, and there is one bit pattern for the uncorrupted codeword. There are 2k+r possible bit patterns, and so the following relation must hold:
possible two-bit error pat-terns, and there is one bit pattern for the uncorrupted codeword. There are 2k+r possible bit patterns, and so the following relation must hold:
Since a Hamming distance of 2p + 1 must be maintained to correct p errors, the Hamming distance for this DEC code must be at least 2 ´ 2 + 1 = 5. If we use the same encoding for error detection instead, then we have p + 1 = 5, and since a Hamming distance of p + 1 must be maintained to detect p errors, then p = 4 errors can be detected.