Examples of Assembly Language Programs
The process of writing an assembly language program is similar to the process of writing a high-level program, except that many of the details that are abstracted away in high-level programs are made explicit in assembly language programs. In this section, we take a look at two examples of ARC assembly language programs.
Program: Add Two Integers.
Consider writing an ARC assembly language program that adds the integers 15 and 9. One possible coding is shown in Figure 4-13. The program begins and ends with a .begin/.end pair. The .org pseudo-op instructs the assembler to begin assembling so that the assembled code is loaded into memory starting at location 2048. The operands 15 and 9 are stored in variables x and y, respectively. We can only add numbers that are stored in registers in the ARC (because
only ld and st can access main memory), and so the program begins by loading registers %r1 and %r2 with x and y. The addcc instruction adds %r1 and %r2 and places the result in %r3. The st instruction then stores %r3 in memory location z. The jmpl instruction with operands %r15 + 4, %r0 causes a return to the next instruction in the calling routine, which is the operating sys- tem if this is the highest level of a user’s program as we can assume it is here. The variables x, y, and z follow the program.
In practice, the SPARC code equivalent to the ARC code shown in Figure 4-13 is not entirely correct. The ld, st, and jmpl instructions all take at least two instruction cycles to complete, and since SPARC begins a new instruction at each clock tick, these instructions need to be followed by an instruction that does not rely on their results. This property of launching a new instruction before the previous one has completed is called pipelining, and is covered in more detail in Chapter 9.
Program: Sum an Array of Integers
Now consider a more complex program that sums an array of integers. One pos- sible coding is shown in Figure 4-14. As in the previous example, the program begins and ends with a .begin/.end pair. The .org pseudo-op instructs the assembler to begin assembling so that the assembled code is loaded into memory starting at location 2048. A pseudo-operand is created for the symbol a_start which is assigned a value of 3000.
The program begins by loading the length of array a, which is given in bytes, into %r1. The program then loads the starting address of array a into %r2, and
clears %r3 which will hold the partial sum. Register %r3 is cleared by ANDing it with %r0, which always holds the value 0. Register %r0 can be ANDed with any register for that matter, and the result will still be zero.
The label loop begins a loop that adds successive elements of array a into the partial sum (%r3) on each iteration. The loop starts by checking if the number of remaining array elements to sum (%r1) is zero. It does this by ANDing %r1 with itself, which has the side effect of setting the condition codes. We are interested in the z flag, which will be set to 1 if %r1 = 0. The remaining flags (n, v, and c) are set accordingly. The value of z is tested by making use of the be instruction. If there are no remaining array elements to sum, then the program branches to done which returns to the calling routine (which might be the operating system, if this is the top level of a user program).
If the loop is not exited after the test for %r1 = 0, then %r1 is decremented by the width of a word in bytes (4) by adding -4. The starting address of array a (which is stored in %r2) and the index into a (%r1) are added into %r4, which then points to a new element of a. The element pointed to by %r4 is then loaded into %r5, which is added into the partial sum (%r3). The top of the loop is then revisited as a result of the “ba loop” statement. The variable length is stored after the instructions. The five elements of array a are placed in an area of memory according to the argument to the .org pseudo-op (location 3000).
Notice that there are three instructions for computing the address of the next array element, given the address of the top element in %r2, and the length of the array in bytes in %r1:
This technique of computing the address of a data value as the sum of a base plus an index is so frequently used that the ARC and most other assembly languages have special “addressing modes” to accomplish it. In the case of ARC, the ld instruction address is computed as the sum of two registers or a register plus a 13-bit constant. Recall that register %r0 always contains the value zero, so by specifying %r0 which is being done implicitly in the ld line above, we are wasting an opportunity to have the ld instruction itself perform the address calculation. A single register can hold the operand address, and we can accomplish in two instructions what takes three instructions in the example:
Notice that we also save a register, %r4, which was used as a temporary place holder for the address.
VARIATIONS IN MACHINE ARCHITECTURES AND ADDRESSING
The ARC is typical of a load/store computer. Programs written for load/store machines generally execute faster, in part due to reducing CPU-memory traffic by loading operands into the CPU only once, and storing results only when the computation is complete. The increase in program memory size is usually considered to be a worthwhile price to pay.
Such was not the case when memories were orders of magnitude more expensive and CPUs were orders of magnitude smaller, as was the situation earlier in the computer age. Under those earlier conditions, for CPUs that had perhaps only a single register to hold arithmetic values, intermediate results had to be stored in memory. Machines had three-address, two-address, and one-address arithmetic instructions. By this we mean that an instruction could do arithmetic with 3, 2, or 1 of its operands or results in memory, as opposed to the ARC, where all arithmetic and logic operands must be in registers.
Let us consider how the C expression A = B*C + D might be evaluated by each of the three- two- and one-address instruction types. In the examples below, when referring to a variable “A,” this actually means “the operand whose address is A.” In order to calculate some performance statistics for the program fragments below we will make the following assumptions:
• Addresses and data words are 16-bits – a not uncommon size in earlier ma- chines.
• Opcodes are 8-bits in size.
• Operands and opcodes are moved to and from memory one word at a time. We will compute both program size, in bytes, and program memory traffic with these assumptions.
Memory traffic has two components: the code itself, which must be fetched from memory to the CPU in order to be executed, and the data values—operands must be moved into the CPU in order to be operated upon, and results moved back to memory when the computation is complete. Observing these computations allows us to visualize some of the trade-offs between program size and memory traffic that the various instruction classes offer.
Three-Address Instructions
In a three-address instruction, the expression A = B*C + D might be coded as:
which means multiply B by C and store the result at A. (The mult and add operations are generic; they are not ARC instructions.) Then, add D to A (at this point in the program, A holds the temporary result of multiplying B times C) and store the result at address A. The program size is 7×2 or 14 bytes. Memory traffic is 16 + 2x(2×3) or 28 bytes.
Two Address Instructions
In a two-address instruction, one of the operands is overwritten by the result. Here, the code for the expression A = B*C + D is:
The program size is now 3x3x2) or 18 bytes. Memory traffic is 18 + 2×2 + 2x2x3 or 34 bytes.
One Address, or Accumulator Instructions
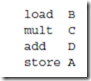
A one-address instruction employs a single arithmetic register in the CPU, known as the accumulator. The accumulator typically holds one arithmetic operand, and also serves as the target for the result of an arithmetic operation. The one-address format is not in common use these days, but was more common in the early days of computing when registers were more expensive and frequently served multiple purposes. It serves as temporary storage for one of the operands and also for the result. The code for the expression A = B*C + D is now:
The load instruction loads B into the accumulator, mult multiplies C by the accumulator and stores the result in the accumulator, and add does the corresponding addition. The store instruction stores the accumulator in A. The pro- gram size is now 2´2´4 or 16 bytes, and memory traffic is 16 + 4´2 or 24 bytes.
Special-Purpose Registers
In addition to the general-purpose registers and the accumulator described above, most modern architectures include other registers that are dedicated to specific purposes. Examples include
• Memory index registers: The Intel 80×86 Source Index (SI) and Destination Index (DI) registers. These are used to point to the beginning or end of an array in memory. Special “string” instructions transfer a byte or a word from the starting memory location pointed to by SI to the ending memory location pointed to by DI, and then increment or decrement these registers to point to the next byte or word.
• Floating point registers: Many current-generation processors have special registers and instructions that handle floating point numbers.
• Registers to support time, and timing operations: The PowerPC 601 processor has Real-Time Clock registers that provide a high-resolution mea- sure of real time for indicating the date and the time of day. They provide a range of approximately 135 years, with a resolution of 128 ns.
• Registers in support of the operating system: most modern processors have registers to support the memory system.
• Registers that can be accessed only by “privileged instructions,” or when in “Supervisor mode.” In order to prevent accidental or malicious damage to the system, many processors have special instructions and registers that are unavailable to the ordinary user and application program. These instructions and registers are used only by the operating system.
PERFORMANCE OF INSTRUCTION SET ARCHITECTURES
While the program size and memory usage statistics calculated above are observed out of context from the larger programs in which they would be contained, they do show that having even one temporary storage register in the CPU can have a significant effect on program performance. In fact, the Intel Pentium processor, considered among the faster of the general-purpose CPUs, has only a single accumulator, though it has a number of special-purpose registers that sup- port it. There are many other factors that affect real-world performance of an instruction set, such as the time an instruction takes to perform its function, and the speed at which the processor can run.