■ SUMMARY
Computer arithmetic can be carried out as we normally carry out decimal arithmetic by hand, while taking the base into account. A two’s complement or a ten’s complement representation is normally used for integers, whereas signed magnitude is normally used for fractions due to the difficulty of manipulating positive and negative fractions in a uniform manner.
Performance can be improved by skipping over 1’s in the Booth and bit-pair recoding techniques. An alternative method of improving performance is to use carryless addition, such as in residue arithmetic. Although carryless addition may be the fastest approach in terms of time complexity and circuit complexity, the more common weighted position codes are normally used in practice in order to simplify comparisons and represent fractions.
■ FURTHER READING
(Goldberg, 1990) is a concise but thorough source of numerous aspects of computer arithmetic. (Hamacher et al., 1990) provides a classic treatment of integer arithmetic. (Flynn, 1970) gives an early treatment of division by zero finding. (Garner, 1959) gives a complete description of the residue number system, whereas (Koren, 1993) gives a more tutorial treatment of the subject. (Huang and Goodman, 1979) describes how a memory based residue processor can be constructed. Koren (1993) also provides additional details on cascading carry-lookahead units. (Cochran, 1968) is a good source for the programming of the HP9100A calculator.
Cochran, D. S., “Internal Programming of the 9100A Calculator,” Hewlett-Pack- ard Journal, (Sept. 1968); Also see http://www.hpmuseum.org/jour- nals/9100:prg.htm.
Flynn, M. J., “On division by functional iteration,” IEEE Trans. Comp., C-19, no. 8, pp. 702-706, (Aug. 1970).
Garner, H. L., “The Residue Number System,” IRE Transactions on Electronic Computers, vol. 8, pp. 140-147, (Jun. 1959).
Goldberg, D., “Computer Arithmetic,” in Patterson, D. A. and J. L. Hennessy, Computer Architecture: A Quantitative Approach, 2/e, Morgan Kaufmann, (1995).
Hamacher, V. C., Z. G. Vranesic, and S. G. Zaky, Computer Organization, 3/e, McGraw Hill, (1990).
Huang, A. and J. W. Goodman, “Number Theoretic Processors, Optical and Electronic,” SPIE Optical Processing Systems, vol. 185, pp. 28-35, (1979).
Koren, I., Computer Arithmetic Algorithms, Prentice Hall, Englewood Cliffs, (1993).
■ PROBLEMS
3.1 Show the results of adding the following pairs of five-bit (i.e. one sign bit and four data bits) two’s complement numbers and indicate whether or not overflow occurs for each case:
3.2 One way to determine that overflow has occurred when adding two numbers is to detect that the result of adding two positive numbers is negative, or that the result of adding two negative numbers is positive. The overflow rules are different for subtraction: there is overflow if the result of subtracting a negative number from a positive number is negative or the result of subtracting a positive number from a negative number is positive.
Subtract the numbers shown below and determine whether or not an overflow has occurred. Do not form the two’s complement of the subtrahend and add: perform the subtraction bit by bit, showing the borrows generated at each position:
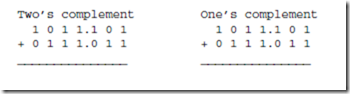
3.3 Add the following two’s complement and one’s complement binary numbers as indicated. For each case, indicate if there is overflow.
3.4 Show the process of serial unsigned multiplication for 1010 (multiplicand) multiplied by 0101 (multiplier). Use the form shown in Figure 3-12.
3.5 Show the process of serial unsigned multiplication for 11.1 (multiplicand) multiplied by 01.1 (multiplier) by treating the operands as integers. The result should be 101.01.
3.6 Show the process of serial unsigned division for 1010 divided by 0101.
Use the form shown in Figure 3-15.
3.7 Show the process of serial unsigned division for 1010 divided by 0100, but instead of generating a remainder, compute the fraction by continuing the process. That is, the result should be 10.12.
3.8 The equation used in Section 3.5.1 for c4 in a carry lookahead adder assumes that c0 is 0 for addition. If we perform subtraction by using the addition / subtraction unit shown in Figure 3-6, then c0 = 1. Rewrite the equation for c4 when c0 = 1.
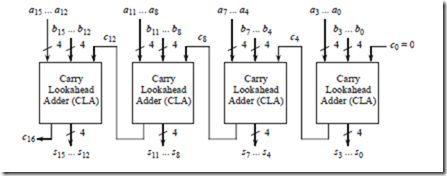
3.9 The 16-bit adder shown below uses a ripple carry among four-bit carry lookahead adders.
(a) What is the longest gate delay through this adder?
(b) What is the shortest gate delay through this adder, from any input to any output?
(c) What is the gate delay for s12?
3.10 Use the Booth algorithm (not bit pair recoding) to multiply 010011 (multiplicand) by 011011 (multiplier).
3.11 Use bit pair recoding to multiply 010011 (multiplicand) by 011011 (mul- tiplier).
3.12 Compute the maximum gate delay through a 32-bit carry lookahead adder.
3.13 What is the maximum number of inputs for any logic gate in a 32-bit carry lookahead adder, using the scheme described in this chapter?
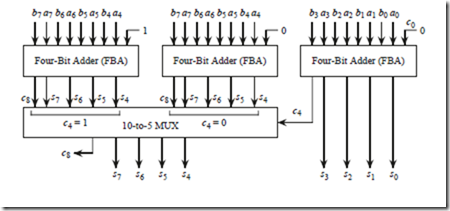
3.14 In a carry-select adder a carry is propagated from one adder stage to the next, similar to but not exactly the same as a carry lookahead adder. As with many other adders, the carry out of a carry-select adder stage is either 0 or 1. In a carry-select adder, two sums are computed in parallel for each adder stage: one sum assumes a carry-in of 0, and the other sum assumes a carry-in of 1.
The actual carry-in selects which of the two sums to use (with a MUX, for example). The basic layout is shown below for an eight-bit carry-select adder:
Assume that each four-bit adder (FBA) unit uses carry lookahead internally. Compare the number of gate delays needed to add two eight-bit numbers using FBA units in a carry-select configuration vs. using FBA units in which the carry is rippled from one FBA to the next.
(a) Draw a diagram of a functionally equivalent eight-bit carry lookahead configuration using the FBAs shown above.
(b) Show the number of gate delays for each adder configuration, by both the 8-bit carry-select adder shown above and the adder designed in part (a) above.
3.15 The path with the maximum gate delay through the array multiplier shown in Figure 3-22 starts in the top right PP element, then travels to the bottom row, then across to the left. The maximum gate delay through a PP element is three. How many gate delays are on the maximum gate delay path through an array multiplier that produces a p-bit result?
3.16 Given multiplication units that each produce a 16-bit unsigned product on two unsigned 8-bit inputs, and 16-bit adders that produce a 16-bit sum and a carry-out on two 16-bit inputs and a carry-in, connect these units so that the overall unit multiplies 16-bit unsigned numbers, producing a 32-bit result.
3.17 Using Newton’s iteration for division, we would like to obtain 32 bits of
precision. If we use a lookup table that provides eight bits of precision for the initial guess, how many iterations need to be applied?
3.18 Add (641)10 to (259)10 in unsigned BCD, using as few digits in the result as necessary.
3.19 Add (123)10 and (-178)10 in signed BCD, using four digit words.