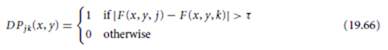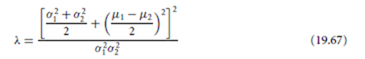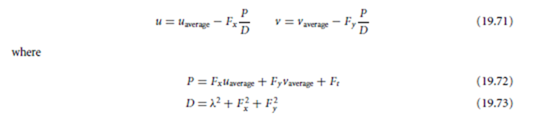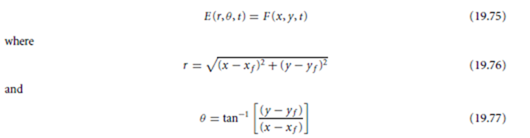19.4.1 Three-Dimensional Object Recognition
The real world that we see and touch is primarily composed of three-dimensional solid objects. When an object is viewed for the first time, people typically gather information about that object from many different viewpoints. The process of gathering detailed object information and storing that information is referred to as model formation. Once a person is familiar with many objects, the objects are then identified from an arbitrary viewpoint without further investigation. People are also able to identify, locate, and qualitatively describe the orientation of objects in black-and-white photographs. This basic capability is significant to machine vision because it involves the spatial variation of a single parameter within a framed rectangular region that corresponds to a fixed, single view of the world.
Recognition System Components
Recognition implies awareness of something already known. In modeling real-world objects for recognition purposes, different kinds of schemes have been used. To determine how recognition will take place, a method for matching model data to sensor data must be considered. A straightforward blind-search approach would entail (1) transforming all possible combinations of all possible known object models in all possible distinguishable orientations and locations into a digitized sensor format and (2) matching based on the minimization of a matching-error criterion. Clearly, this approach is impractical. On the other hand, since object models contain more object information than sensor data, we are prohibited from transforming sensor data into complete model data and matching in the model data format. However, this does not prevent us from matching with partial model data. As a result, working with an intermediate domain that is computable from both sensor and model data is advantageous. This domain is referred to as the symbolic scene description domain. A matching procedure is carried out on the quantities in this domain, which are referred to as features.
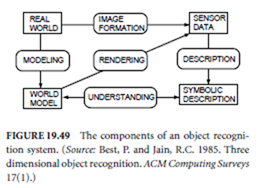
The interactions between the individual components of a recognition system are illustrated in Fig. 19.49. The image formation process creates intensity or range data based purely on physical principles. The description process acts on the sensor data and extracts relevant application-independent features. This process is completely data-driven and includes only the knowledge of the image formation process. The modeling process provides object models for real-world objects. Object reconstruction from sensor data is one method for building models automatically. The understanding, or recognition, process involves an algorithm to perform matching between model and data descriptions. This process might include data- and model-driven sub- processes, where segmented sensor data regions seek explanations in terms of models and hypothesized models seek verification from the data. The rendering process produces synthetic sensor data from object models. Rendering provides an important feedback link by allowing an autonomous system to check on its own understanding of the sensor data by comparing synthetic images to sensed images.
Object Representation Schemes
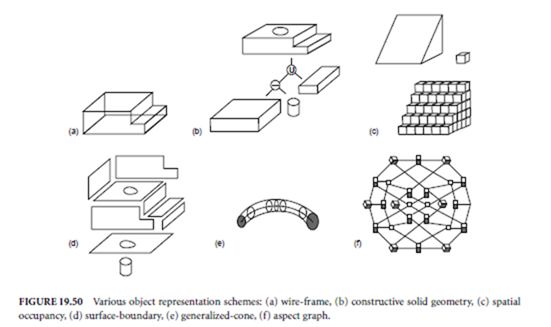
Numerous schemes have been developed for representing three-dimensional objects. The choice of a particular scheme is governed by its intended application. In computer graphics, schemes such as the wire-frame and constructive solid-geometry representations are popular since their data structures are suitable for image rendering. In machine vision systems, other methods such as generalized cones and characteristic views are used extensively. In the following, we briefly describe some commonly used object representation schemes.
Wire Frame
The wire-frame representation of a three-dimensional object consists of a three-dimensional vertex point list and an edge list of vertex pairs. Although this representation is very simple, it is an ambiguous representation for determining such quantities as surface area and volume of an object. Wire-frame
models can sometimes be interpretted as several different solid objects or as different orientations of the same object. Figure 19.50(a) shows the wire-frame representation of a simple three-dimensional object.
Constructive Solid Geometry
The constructive solid-geometry (CSG) representations of an object is specified in terms of a set of three- dimensional volumetric primitives (blocks, cylinders, cones, spheres, etc.) and a set of boolean operators: union, intersection, and difference. Figure 19.50(b) shows the CSG representation for a simple geometric object. The storage data structure is a binary tree, where the terminal nodes are instances of the geometric primitives and the branching nodes represent the Boolean set operations and positioning information. CSG trees define object surface area unambiguously and can, with very little data, represent complex objects. However, the boundary evaluation algorithms required to obtain usable surface information are very computationally expensive. Also, general sculptured surfaces are not easily represented using CSG models.
Spatial Occupancy
Spatial-occupancy representations use nonoverlapping subregions of three-dimensional space occupied by an object to define that object. This method unambiguously defines an object’s volume. Some commonly used single primitive representations of this type are the voxel and octree representations. Voxels are small volume elements of discretized three-dimensional space (see Fig. 19.50(c)). They are usually fixed-size cubes. Objects are represented by the lists of voxels occupied by the object. Voxel representations tend to be very memory intensive, but algorithms using them tend to be very simple. An octree is a hierarchical representation of spatial occupancy. Volumes are decomposed into cubes of different size, where the cube size depends on the distance from the root node. Each branching node of the tree represents a cube and points to eight other nodes, each of which describes object volume occupancy in the corresponding octant subcubes of the branching node cube. The octree representation offers the advantages of the voxel description but is more compact. Beacuse of this compactness, more complicated algorithms are required for many computations than those needed for voxel representation.
Surface Boundary
The surface-boundary representation defines a solid object by defining the three-dimensional surfaces that bound the object. Figure 19.50(d) shows a surface-boundary representation for a simple geometric object. The simplest boundary representation is the triangle-faced polyhedron, which can be stored as a list of three-dimensional triangles. Arbitrary surfaces are approximated to any desired degree of accuracy by utilizing many triangles. A slightly more compact representation allows the replacement of adjacent, connected, coplanar triangles with arbitrary n-sided planar polygons. Structural relationships between bounding surfaces may also be included as part of the model.
Generalized Cone
In the generalized-cone (generalized-cylinder or sweep) representation, an object is represented by a three-dimensional space curve that acts as a spine or axis of the cone, a two-dimensional cross-sectional figure, and a sweeping rule that defines how the cross section is to be swept (and possibly modified) along the space curve (see Fig. 19.50(e)). Generalized cones are well suited for representing many real-world shapes. However, certain objects, such as the human face or an automobile body, are difficult to represent as generalized cones. Despite its limitations, the generalized-cone representation is popular in machine vision.
Skeleton
Skeleton representations use space-curve skeletons. A skeleton can be considered an abstraction of the generalized cone description that consists of only the spines. Skeleton geometry provides useful abstract information. If a radius function is specified at each point on the skeleton, this representation is capable of general-purpose object description.
Multiple Two-Dimensional Projection
For some applications, a library of two-dimensional silhouette projections that represent three-dimensional objects can be conveniently stored. For the recognition of three-dimensional objects with a small number of stable orientations on a flat table, this representation is ideal—if the object silhouettes are sufficiently different. For example, silhouettes have been used to recognize aircraft in any orientation against a well-lit sky background. However, because many different three-dimensional-object shapes can possess the same silhoutte projection, this type of representation is not a general-purpose technique.
Aspect Graphs
In the aspect graph representation, the space of viewpoints is partitioned into maximal regions, where every viewpoint in each region gives the same qualitative view of the object, called the aspect. Within each region, projections of the object will have the same number and types of features, with identical spatial relationships among them. However, the quantitative properties of these features, such as lengths of edges, vary with the change in viewpoint. Changes in the aspect, called visual events, take place at the boundaries between regions. Two aspects are said to be connected by a visual event if their corresponding regions are adjacent in the viewpoint space. An aspect graph is a graph structure whose nodes represent aspects and their associated regions and whose arcs denote the visual events and boundaries between adjacent regions. Figure 19.50(f) shows the aspect graph for a cube.
Characteristic Views
A concept very similar to aspect graphs is that of characteristic views. All of the infinite two-dimensional perspective projection views of an object are grouped into a finite number of topologically equivalent classes. Different views within an equivalence class are related via linear transformations. A representative member of an equivalence class is called the characteristic view for that class. In this scheme, objects are assumed to rest on a supporting plane; hence, they are restricted to appear in a number of stable positions. Characteristic views of objects are derived with certain constraints on the camera configuration. It is this use
of camera position and orientation information that differentiates the characteristic view representation scheme from the aspect graph. Because characteristic views specify the three-dimensional structure of an object, they also provide a general-purpose object representation.
19.4.2 Dynamic Vision
Early machine vision systems were concerned primarily with static scenes; however, the world is dynamic. Designing machine vision systems capable of analyzing dynamic scenes is increasingly becoming more popular. For a machine vision system engaged in the performance of nontrivial real-world operations and tasks, the ability to cope with moving and changing objects and viewpoints is vital.
The input to a dynamic-scene analysis system is a sequence of image frames. The camera used to acquire the image sequence may itself be in motion. Each frame represents an image of the scene at a particular instant in time. The changes in a scene may be due to camera motion, object motion, illumination changes, or changes in object structure, size, or shape. Changes in a scene are usually assumed to be due to camera and/or object motion; objects are usually assumed to be either rigid or quasirigid. Other changes are not allowed.
A scene usually contains several objects. An image of the scene at a given time represents a projection of part of the scene; the part of the scene depends on the position of the camera. Four cases represent the possibilities for the dynamic-camera/world setup:
1. Stationary camera, stationary objects (SCSO)
2. Stationary camera, moving objects (SCMO)
3. Moving camera, stationary objects (MCSO)
4. Moving camera, moving objects (MCMO)
The first case is simple static-scene analysis. In many applications, processing a single image to obtain the required information may be feasible. However, many more applications exist that require information to be extracted from a dynamic environment.
Clearly, a sequence of image frames offers much more information to aid in scene understanding, but significantly increases the amount of data to be processed by the system. Applying static-scene analysis techniques to each frame of a sequence requires an enormous amount of computation, while still suffering from all of the problems of static-scene analysis. Fortunately, research in dynamic-scene analysis has shown that information recovery may be easier in dynamic scenes than in static scenes. In some cases, the total computational effort may be significantly less and the performance is better.
SCMO scenes have received the most attention in dynamic-scene analysis. The objectives of such scene analysis usually are to detect motion, to extract masks of moving objects with the aim of recognizing them, and to compute their motion characteristics. MCMO is the most general case and possibly presents the most difficult situation in dynamic-scene analysis. Many techniques that have been developed assuming a stationary camera are not applicable to a moving camera. Likewise, techniques developed for a moving camera generally assume a stationary scene and are usually not applicable if the objects are moving. SCMO and MCSO have found uses in many applications and have been studied by researchers in various contexts under various assumptions.
Change Detection
Any perceptable motion in a scene results in some change in the sequence of frames of the scene. If such changes are detected, motion characteristics can be analyzed. A good quantitative estimate of the motion components of an object can be obtained if the motion is restricted to a plane that is parallel to the image plane; for three-dimensional motion, only qualitative estimates are possible. By analyzing frame-to-frame differences, a global analysis of the sequence can be performed. Changes can be detected at different levels: pixel, edge, or region.
Difference Pictures
The most obvious method of detecting change between two frames is to directly compare the corresponding pixels of the frames to determine whether or not they are the same. In the simplest form, a binary difference picture D P jk (x, y) between frames j and k is obtained by
where τ is a threshold and F (x, y, j ) and F (x, y, k) are the image arrays of the j th and kth frames, respectively.
In the difference picture, pixels that have a value of 1 may be considered to be the result of object motion. Because of noise, however, such a simple test on real scenes usually produces unsatisfactory results. A simple size filter may be used to ignore pixels not forming a connected cluster of minimal size. Then only those pixels in the difference picture with the value of 1 that belong to a four-connected (or eight-connected) component larger than a set number of pixels will be attributed to object motion. This filter is very effective in reducing noise, but unfortunately it also filters some desirable signals, such as those from small or slowly moving objects.
Likelihood Ratio
To make change detection more robust, regions or groups of pixels at the same location in two frames may be considered and their intensity characteristics may be compared more rigorously. One method using this approach is based on comparing the frames using the likelihood ratio. Thus, we can compute the difference picture by replacing |F (x, y, j ) − F (x, y, k)| with λ where
and µ and σ denote the mean gray value and the square root of the variance from the frames for the sample area, respectively.
The likelihood ratio can only be applied to regions and not to single pixels. This limitation presents a minor problem, which can be solved by considering corresponding areas of the frames. The likelihood ratio test, combined with a size filter, works well for noise removal in many real-world scenes. The likelihood ratio test can be applied to every point in each frame by considering overlapping areas centered on each pixel of the image, or to a subsampling of points by using nonoverlapping areas, called superpixels.
Accumulative Difference Pictures
The problem of missing the detection of small or slowly moving objects can be solved by analyzing change over a series of frames, instead of just between two frames. The accumulative difference picture (ADP) is used to detect the motion of small and slowly moving objects. An accumulative difference picture is formed by comparing every frame in an image sequence to a common reference frame. The entry in the accumulative difference picture is increased by one whenever the likelihood ratio for that region exceeds the threshold. Thus, an accumulative difference picture acquired over k frames is given by
where the first frame of a sequence is usually the reference frame.
Time-Varying Edge Detection
As a result of the importance of edge detection in static scenes, it is reasonable to expect that time- varying edge detection may also be important in dynamic-scene analysis. Moving edges can be detected by combining the spatial and temporal gradients using a logical AND operation, which is implemented
through multiplication. Thus, the time-varying edgeness of a point in a frame is given by
where dF /dS and dF /dt are the magnitudes of the spatial and temporal gradients of the intensity at point (x, y, t), respectively. Various conventional edge detectors can be used to compute the spatial gradient, and a simple difference can be used to compute the temporal gradient. In most cases, this edge detector works effectively. By applying a threshold to the product—rather than first differencing and then applying an edge detector, or first detecting edges and then computing their temporal gradient—this method overcomes the problem of missing weak or slowly moving edges.
Optical Flow
Optical flow is the distribution of velocity, relative to the observer, over the points of an image. Optical flow carries information that is valuable in dynamic-scene analysis. Optical flow is determined by the velocity vector at each pixel in an image. Several methods have been devised for calculating optical flow based on two or more frames of a sequence. These methods can be classified into two general categories: feature based and gradient based. If a stationary camera is used, most of the points in an image frame will have zero velocity. This is assuming that a very small subset of the scene is in motion, which is usually true. Thus, most applications for optical flow involve a moving camera.
Feature-Based Methods
Feature-based methods for computing optical flow first select some features in consecutive image frames, match these features between frames, and then calculate the disparities between them. As mentioned earlier, the correspondence problem can be solved using relaxation. However, the problem of selecting features and establishing correspondence is not easy. Moreover, this method only produces velocity vectors at sparse points within the image.
Gradient-Based Methods
Gradient-based methods exploit the relationship between the spatial and temporal gradients of image intensity. This relationship can be used to segment images based on the velocity of image points. The relationship between the spatial and temporal gradients and the velocity components is
where u = dx/dt and v = dy/dt. In this equation, Fx , F y , and Ft represent the spatial gradients in the x and y directions and the temporal gradient, respectively, and can be computed directly from the image. Then, at every point in an image, there are two unknowns, u and v , yet there is only one equation. Thus, optical flow cannot be directly determined.
The velocity field, however, can be assumed to vary smoothly over an image. Under this assumption, an iterative approach for computing optical flow using two or more frames can be utilized. The following iterative equations are used for the computation of image flow:
where λ is a constant multiplier. When only two frames are used, the computation is iterated over the same frames many times. For more than two frames, each iteration uses a new frame.
Segmentation Using a Moving Camera
If the camera is moving, then every point in the image has nonzero velocity relative to the camera (except the case where object points are moving with the same velocity as the camera). The velocity relative to the camera depends on both the velocity of the point itself and the distance of the point from the camera. Approaches based on differences may be extended for segmenting moving-camera scenes. If the aim is to extract images of moving objects, however, then additional information is required to decide whether the motion at a point is due solely to its depth or is due to a combination of its depth and its motion. Gradient-based approaches will also require additional information.
If the camera’s direction of motion is known, the focus of expansion (FOE) with respect to the stationary components in the scene can easily be computed. The FOE will have coordinates (x f , y f ) where
in the image plane. The velocity vectors of all stationary points in a scene project onto the image plane so that they intersect at the FOE. A transformation with respect to the FOE can be used to simplify the task of segmentation. The ego-motion polar (EMP) transformation of an image transforms a frame F (x, y, t) into E (r, θ, t) using
In EMP space, stationary points are displaced only along the θ axis between the frames of an image sequence, whereas points on moving objects are displaced along the r axis as well as the θ axis. Thus, the displacement in EMP space can be used to segment a scene into its stationary and nonstationary components. Moreover, when complex logarithmic mapping (CLM) is performed about the FOE, interesting points in the EMP space can be obtained.