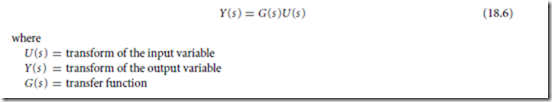Process Dynamics and Control
Introduction
The field of process dynamics and control is concerned with the analysis of dynamic behavior of processes, process simulation, design of automatic controllers, and associated instrumentation. Process control as practiced in the process industries has undergone significant changes since it was first introduced in the 1940s. Perhaps the most significant influence on the changes in process control technology has been the introduction of digital computers and instruments with greater capabilities than their analog predecessors. During the past 25 years automatic control has assumed increased importance in the process industries, which has led to the application of more sophisticated techniques (Seborg, Edgar, and Mellichamp, 2004; Ogunnaike and Ray, 1995).
For instrumenting and controlling a modern plant, it is necessary that an engineer has an understanding of the time-dependent behavior of typical processes. This in turn requires an appreciation of how mathematical tools can be employed in analysis and design of automatic control systems. In this chapter we present the basic ideas involved in developing dynamic models for typical processes and then discuss the use of control valves and proportional-integral-derivative (PID) feedback controllers for process control. Next, various types of advanced control methods that have seen commercial use are reviewed. Finally, some comments on computer control are included. For a thorough discussion of process instrumentation and measurement devices, the reader is referred to other entries in the section, “Control and Instrumentation Technology,” in this handbook.
Objectives of Process Control
The main economic objective of process control is to achieve maximum productivity or efficiency while maintaining a satisfactory level of product quality. Manufacturing facilities in the production of chemicals, paper, metals, power, food, and pharmaceuticals require accurate and precise control systems. Although the methods of production vary from industry to industry, the principles of automatic control are generic in nature and can be universally applied, regardless of the size of the plant.
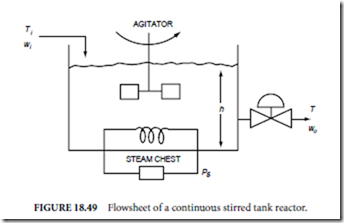
Consider the control of the stirred tank reactor shown in Fig. 18.49. This system can be used to introduce basic concepts and definitions in process control, as given by the following:
1. Controlled variables: These are the variables that quantify the performance or quality of the final product, which are also called output variables. In Fig. 18.49, the controlled variables are the tank temperature T and the liquid level in the tank h. Controlling the temperature allows the chemical reaction to proceed at a specified rate. The tank level determines the residence time in the reactor. The desired operating point for each controlled variable is called the set point.
2. Manipulated variables: These input variables are adjusted dynamically to keep the controlled variables at their setpoints. There are two manipulated variables in Fig. 18.49, namely, the exit flow rate wo and the steam pressure Ps to the heat transfer coil in the tank.
3. Disturbance variables: These are also called load variables and represent input variables that can cause the controlled variables to deviate from their respective set points. For the stirred tank heater, both the feed rate wi and feed temperature Ti can change, causing the tank level and exit temperature to move away from the set points.
In the design of controllers for this process, two cases can be evaluated:
1. Set point change: This involves carrying out a change in the operating conditions, e.g., from a tank exit temperature of 125 to 150◦C while holding the level constant. The set-point signal is changed, and the heat transfer rate is adjusted appropriately to achieve the new operating conditions. The changing of set points is also called servomechanism (or servo) control, and it can require a time span as short as a few seconds to as long as several hours to carry out, depending on the process design variables. In Fig. 18.49, such design variables could include the flow rate and the tank holdup.
2. Disturbance change: This case relates to the process transient behavior when a disturbance enters, also called regulatory control. A control system should be able to return each controlled variable back to its set point.
Several other definitions need to be discussed here. Steady-state behavior pertains to the case where there is no variation in the process variables with respect to time. If the system is in equilibrium (at steady state), it can be described by algebraic equations, such as material and energy balances. Unsteady-state (dynamic) behavior occurs when the process variables change as a function of time. The required mathematical model for this case includes ordinary differential equations as well as algebraic relationships.
Three further classifications deal with how process control is implemented, namely:
✁ Open-loop or manual control
✁ Closed-loop or feedback control
✁ Feedforward control
Manual control implies that the operator makes the changes in manipulated variable, which is used occasionally. Feedback control connotes that the manipulated variable is changed automatically in response to the error between the set point and controlled variable. The second approach serves as the basis for most automatic control schemes. Feedforward control is a technique where the manipulated variable is changed as a function of a disturbance variable. Both feedback and feedforward control are discussed in later sections of this chapter.
Development of a Mathematical Model
There are a number of modeling approaches that can be used with process control systems. Whereas mathematical models based on the chemistry and physics of the system represent one alternative, the typical process control model utilizes an empirical input/output relationship, the so-called black-box model. These models are found by experimental tests of the process. Mathematical models of the control system may include not only the process but also the controller, the final control element, and other electronic components such as measurement devices and transducers. Once these component models have been determined, one can proceed to analyze the overall system dynamics, the effect of different controllers in the operating process configuration, and the stability of the system, as well as obtain other useful information.
Mathematical models provide a convenient and compact way of expressing the behavior of a process as a function of process physical parameters and process inputs. The same mathematical model can be expressed in several ways; for example, a continuous-time model based on a differential equation can be converted to a discrete-time system, or it can be transformed to a different type of independent variable altogether (e.g., Laplace transforms or z transforms). Transform models generally feature a simplified notation, which greatly facilitates analysis of complicated systems.
A simple dynamic system with one input and one output can be represented by equations of the form
where y is the output, u is the input, and t is time. The time solution to this equation can be found by integrating Eq. (18.1) for a given input u(t), based on a specified initial condition for the output y(0). By letting dy/dt = 0, steady-state or equilibrium value(s) of y can be found for each selected value of u, the input, by solving the algebraic equation
Theoretical models of chemical processes normally involve sets of nonlinear differential equations that arise from mass and energy balances, thermodynamics, reaction kinetics, transport phenomena, and physical property relationships. Because of the difficulty of developing such theoretical models, simpler models are usually sought for the purposes of control, either by linearization of the nonlinear models or by making simplifying assumptions. On the other hand, a less time-consuming approach involves developing black box models, which are obtained by fitting experimental input-output data. This latter approach has been the historical basis of process control practice. During the past 10 years, however, there has been increasing use of fundamental models in design and control, largely due to the availability of modeling software packages.
Denoting K as the process gain, the simplest dynamic model used in process control is a first-order linear differential equation:
where τ is the time constant and K is the process gain.
At steady state, yss = K u. Linear dynamic models such as Eq. (18.3) provide a theoretical means to determine the time scale of the process. For a step change in u (= M), the solution to Eq. (18.3) can be found analytically,
From Eq. (18.4) we can conclude that the response of y reaches 63.2% of its final value when t = τ (1 − e−1) = 0.632. In this way, τ determines the speed of response for the system.
Experience in the process industries indicates that there are a limited number of expected dynamic behaviors that actually influence the controller design step. These behaviors can be categorized using the step response and are based on a transfer function representation of the process model, which is assumed to be linear or a linear approximation of a nonlinear model. A transfer function is found by taking the Laplace transform of the ordinary differential equation that describes the system; the mathematical definition of the Laplace transform is
where f (t) is a specified function of time.
The chief mathematical advantage of the Laplace transform is the conversion of the differential equation (such as Eq. (18.1)) to an algebraic equation. The resulting equation can be rearranged as a transfer function,
G (s ) describes the dynamic characteristics of the process. For linear systems it is independent of the input variable, so it applies for any time-dependent input signal. For the model in Eq. (18.3), the transfer function is
where K is the process gain and τ the time constant already mentioned.
Transfer functions can also be used to describe the dynamic behavior of instruments, controllers, and valves. For a temperature transmitter the steady-state gain is simply the output span divided by the input span; an electronic transmitter which has a 4–20 mA output and a 100–200◦F temperature input range gives a gain of (20 − 4)/(200 − 100) = 0.16 mA/◦F. Sensors usually have simple dynamics, typically described by a first-order transfer function. The characteristics of control valves are more complicated and are discussed in the next section.
The order of the transfer function is the power of the polynomial in s in the denominator of G (s ) and is equivalent to the order of the differential equation describing the process. There are a limited number of dynamic transfer functions that are important for process control; Fig. 18.50 shows the dynamic response
of nine different cases that result from a step change in the input variable. Simple approximate models are usually developed from experimental tests, and the model parameters are fitted either graphically or by nonlinear regression. In Fig. 18.50 only first- and second-order models are used. Some comments on each case are given next:
Case 1
This is the first-order system discussed previously, which is the analog of a resistance-capacitance circuit in electronics. It is mainly applicable to responses of instruments (sensors and valves) but usually is inadequate to describe dynamic behavior of actual chemical processes.
Case 2
The second-order system response provides a better approximation for many real processes dynamics, such as chemical reactors and distillation columns.
Case 3
Overshoot can occur in some open-loop systems as shown here, but this case is relatively rare. Some controllers exhibit this behavior.
Case 4
This behavior is called inverse response, where the output initially goes the opposite direction to the final value. This wrong-way behavior is seen in boilers and distillation columns.
Case 5
Pure delay or dead time usually occurs due to transportation lag, such as flow through a pipe. For a velocity
v and distance L , θ = L /v . Another case is a measurement delay, such as for a gas or liquid chromatograph.
Case 6
This is a more realistic response than case 1 because it allows for a time delay as well as first-order behavior, and can be applied to many chemical processes. The delay time may not be clearly identified as transport lag but may be imbedded in higher order dynamics. Hence, this is an approximate but very useful model, especially for staged systems such as distillation or extraction columns. An extension of this model is second order plus time-delay, the response of which is equivalent to case 2 or case 4 with an initial time delay. The advantage over first-order models is that an additional model parameter can give greater accuracy in fitting process data.
Case 7
The integrator describes the behavior of level systems, where the step input (such as a flow change) causes the level to increase with constant slope until the flow is reduced to its original value. There is no time constant here because the level does not reach steady state for a step input but continues to increase until the step input is terminated (or the vessel overflows).
Case 8
Oscillation in the step response is rare for chemical processes under open-loop or manual conditions. When feedback control is implemented, with processes described by cases 2–6, the occurrence of oscillation is quite common. In fact, a well-tuned feedback controller exhibits some degree of oscillation, as discussed later. The time constants for this case are not real values but are imaginary numbers.
Case 9
If any time constant is negative (τ in this case is not physically meaningful), the response is unstable. The output response becomes larger with time and is unbounded. No real system actually behaves this way since some constraint will eventually be reached; for example, a safety valve will open. A linear process is at the limit of instability if it oscillates without decay. Most processes are stable and do not require a controller for stability; however, such self-regulating processes may exhibit very slow responses unless feedback control is applied. On the other hand, when feedback control is used with some processes, instability can occur if the controller is incorrectly designed (see later discussion on controller tuning). There are a few processes, such as chemical reactors, which may be unstable in the open loop, but these can be stabilized by feedback control.
In summary, with all of the various dynamic behaviors shown in Fig. 18.50, it is important for plant engineers, instrument specialists, and even some operators to understand the general dynamic character- istics of a process. It is also crucial that they know how various processes respond under the influence of feedback control.