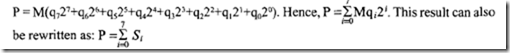8.4.2 Pipeline Processing
The purpose of this section is to provide a brief overview of pipelining.
Basic Concepts
Assume a task T is carried out by performing four activities: AI, A2, A3, and A4, in that order. Hardware Hi is designed to perform the activity Ai. Hi is referred to as a segment, and it essentially contains combinational circuit elements. Consider the arrangement shown in Figure 8.45.
In this configuration, a latch is placed between two segments so the result computed
by one segment can serve as input to the following segment during the next clock period. The execution of four tasks Tl, T2, T3, and T4 using the hardware of Figure 8.45 is described using a space-time chart shown in Figure 8.46.
Initially, task Tl is handled by segment I. After the first clock, segment 2 is busy with Tl
while segment 1 is busy with T2. Continuing in this manner, the task Tl is completed at the end of the fourth clock. However, following this point, one task is shipped out per clock. This is the essence of the pipeline concept. A pipeline gains efficiency for the same reason as an assembly line does: Several activities are performed but not on the same material. Suppose ti and L denote the propagation delays of segment i and the latch, respectively. Then the pipeline clock period T can be expressed as follows:
T = max (Tl, T2, … Tn) + L
The segment with the maximum delay is known as the bottleneck, and it decides the pipeline clock period T. The reciprocal ofT is referred to as the pipeline frequency.
Consider the execution of m tasks using an n-segment pipeline. In this case, the
first task will be completed after n clocks (because there are n segments) and the remaining m-1 tasks are shipped out at the rate of one task per pipeline clock.
Therefore, n + (m – 1) clock periods are required to complete m tasks using an n-s egment pipeline. If all m tasks are executed without any overlap, mn clock periods are needed because each task has to pass through all n segments. Thus speed gained by an n segment pipeline can be shown as follows:
P(n) approaches n when m approaches infinity. This implies that when a large number of tasks are carried out using ann-segment pipeline, ann-fold increase in speed can be expected.
The previous result shows that the pipeline completes m tasks in the m + n – 1 clock periods. Therefore, its throughput can be defined as follows:
For a large value of m, U(n) approaches 1/T, which is the pipeline frequency. Thus the throughput of an ideal pipeline is equal to the reciprocal of its clock period. The efficiency of an n-segment pipeline is defined as the ratio of the actual speedup to the maximum speedup realized.
This illustrates that when m is very large, E(n) approaches 1 as expected.
In many modem computers, the pipeline concept is used in carrying out two tasks: arithmetic operations and instruction execution.
Arithmetic Pipelines
The pipeline concept can be used to build high-speed multipliers. Consider the multi plication P = M * Q, where M and Q are 8-bit numbers. The 16-bit product P can be expressed as:
where, S; = Mq;2; and each S; represents a 16-bit partial product. Each partial product is the shifted multiplicand. All 8 partial products can be added using several carry-save adders.
This concept can be extended to design an n x n pipelined multiplier. Here n partial products must be summed with 2n bits per partial product. So, as n increases, the hardware cost associated with a fully combinational multiplier increases in an exponential fashion. To reduce the hardware cost, large multipliers are designed.
The pipeline concept is widely used in designing floating-point arithmetic units. Consider the process of adding two floating point numbers A= 0.9234 * I 04 and B = 0.48 * 102 • First, notice that the exponents of A and Bare unequal. Therefore, the smaller number should be modified so that its exponent is equal to the exponent of the greater number.
For this example, modify B to 0.0048 * 104• This modification step is known as exponent alignment. Here the decimal point of the significand 0.48 is shifted to the right to obtain the desired result. After the exponent alignment, the significands 0.9234 and 0.0048 are added to obtain the final solution of0.9282 * 104•
For a second example, consider the operation A- B, where A= 0.9234 * 104 and B = 0.9230 * 104• In this case, no exponent alignment is necessary because the exponent of A equals to the exponent of B. Therefore, the significand of B is subtracted from the significand of A to obtain 0.9234- 0.9230 = 0.0004. However, 0.0004 * 104 cannot be the final answer because the significand, 0.0004, is not normalized. A floating-point number with base b is said to be normalized if the magnitude of its significand satisfies the following inequality: 1/b lsignificandl < 1.
In this example, since b = 10, a normalized floating-point number must satisfy the condition:
0.1 lsignificandl < I
(Note that normalized floating-point numbers are always considered because for each real world number there exists one and only one floating-point representation. This uniqueness property allows processors to make correct decisions while performing compare operations).
The final answer is modified to 0.4 * 101 • This modification step is known as postnormalization, and here the significand is shifted to the left to obtain the correct result.
In summary, addition or subtraction of two floating-point numbers calls for four activities:
I. Exponent comparison
2. Exponent alignment
3. Significand addition or subtraction
4. Postnormalization
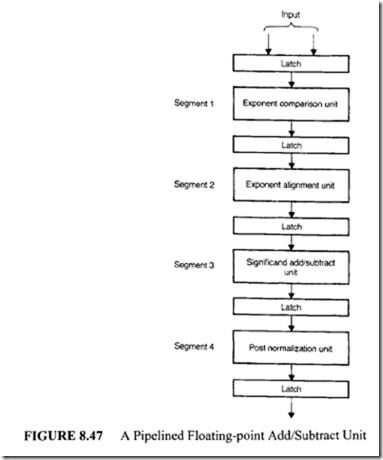
Based on this result, a four-segment floating-point adder/subtracter pipeline can be built, as shown in Figure 8.47.
It is important to realize that each segment in this pipeline is primarily composed of combinational components such as multiplexers. The shifter used in this system is the barrel shifter discussed earlier. Modem microprocessors such as Motorola MC 68040 include a 3-stage floating-point pipeline consisting of operand conversion, execute, and result normalization.
Instruction Pipelines
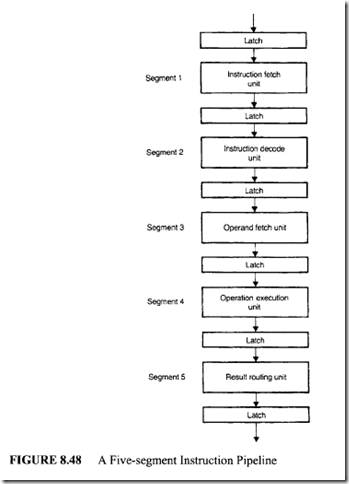
Modem microprocessors such as Motorola MC 68020 contain a 3-stage instruction pipeline. Recall that an instruction cycle typically involves the following activities:
I. Instruction fetch
2. Instruction decode
3. Operand fetch
4. Operation execution 5. Result routing.
This process can be effectively carried out by using the pipeline shown in Figure 8.48. As mentioned earlier, in such a pipelined scheme the first instruction requires five clocks to complete its execution. However, the remaining instructions are completed at a rate of one per pipeline clock. Such a situation prevails as long as all the segments are busy.
In practice, the presence of branch instructions and conflicts in memory accesses poses a great problem to the efficient operation of an instruction pipeline.
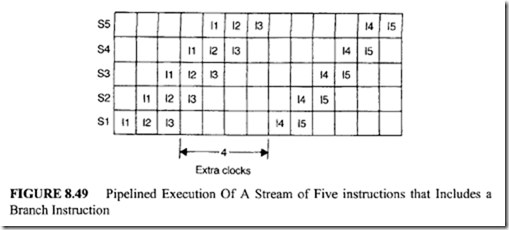For example, consider the execution of a stream of five instructions: I1, 12, 13, 14, and IS in which I3 is a conditional branch instruction. This stream is processed by the instruction pipeline (Figure 8.48) as depicted in Figure 8.49.
When a conditional branch instruction is fetched, the next instruction cannot be
fetched because the exact target is not known until the conditional branch instruction has been executed. The next fetch can occur once the branch is resolved. Four additional clocks are required due to 13.
Suppose a stream of s instructions is to be executed using an n-segment pipeline. If c is the probability for an instruction to be a conditional branch instruction, there will be s c conditional branch instructions in a stream of s instructions. Since each branch instruction requires n – I additional clocks, the total number of clocks required to process a stream of s instructions is
For no conditional branch instructions (c = 0), 5 instructions per instruction cycle are executed. This is the best result produced by a five-segment pipeline. If 25% of the
per instruction cycle can be executed. This shows how pipeline efficiency is significantly decreased even with a small percentage of branch instructions.
·In many contemporary systems, branch instructions are handled using a strategy called Target Prefetch. When a conditional branch instruction is recognized, the immediate successor of the branch instructions and the target of the branch are prefetched. The latter is saved in a buffer until the branch is executed. If the branch condition is successful, one pipeline is still busy because the branch target is in the buffer.
Another approach to handle branch instructions is the use of the delayed branch concept. In this case, the branch does not take place until after the following instruction. To illustrate
this, consider the instruction sequence shown in Figure 8.50.
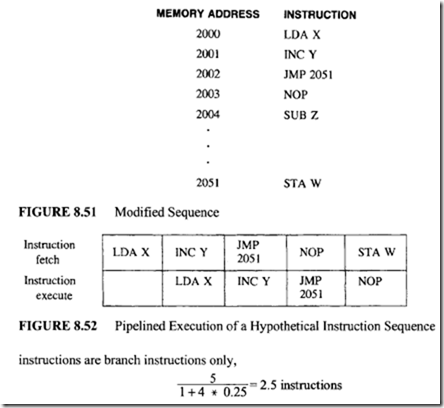
Suppose the compiler inserts a NOP instruction and changes the branch instruction to JMP 2051. The program semantics remain unchanged. This is shown in Figure 8.51.
This modified sequence depicted in Figure 8.51 will be executed by a two-segment pipeline, as shown in Figure 8.52:
-
Instruction fetch
-
Instruction execute
Because of the delayed branch concept, the pipeline still functions correctly without damage.
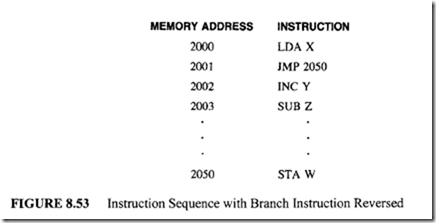
The efficiency of this pipeline can be further improved if the compiler produces a new sequence as shown in Figure 8.53.
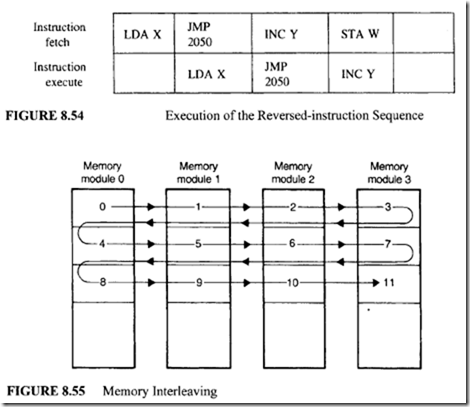
In this case, the compiler has reversed the instruction sequence. The JMP instruction is placed in the location 2001, and the INC instruction is moved to memory location 2002. This reversed sequence is executed by the same 2-segment pipeline, as shown in Figure 8.54.
It is important to understand that due to the delayed branch rule, the INC Y instruction is fetched before the execution of JMP 2050 instruction; therefore, there is no change in the order of instruction execution. This implies that the program will still produce the same result. Since the NOP instruction was eliminated, the program is executed more efficiently.
The concept of delayed branch is one of the key characteristics of RISC as it makes concurrency visible to a programmer.
As does the presence of branch instructions, memory-access conflicts cause damage to pipeline performance. For example, if the instructions in the operand fetch and result-saving units refer to the same memory address, these operations cannot be overlapped.
To reduce such memory conflicts, a new approach called memory interleaving is often employed. For this case, the memory addresses are distributed among a set of memory modules, as shown in Figure 8.55.
In this arrangement, memory is distributed among many modules. Since consecutive addresses are placed into different modules, the CPU can access several words in one memory access.