Number Systems :Binary Coded Decimal and Gray Codes

Binary Coded Decimal

In the early days of programming, data structures were often the result of a curious blend of trying to come up with a data format that best suited the programmer and what best suited the current hardware. One of the more

Table 4-5 Decimal digits with binary and BCD decimal equivalents.

Decimal	Binary	BCD	Decimal	Binary	BCD
0	B’0000’	0	8	B’1000’	8
1	B’0001’	1	9	B’1001’	9
2	B’0010’	2	10	B’1010’	Invalid
3	B’0011’	3	11	B’1011’	Invalid
4	B’0100’	4	12	B’1100’	Invalid
5	B’0101’	5	13	B’1101’	Invalid
6	B’0110’	6	14	B’1110’	Invalid
7	B’0111’	7	15	B’1111’	Invalid

enduring structures that came from this time is the ‘‘binary coded decimal’’ (most often referred to by its acronym ‘‘BCD’’) which used four bits, like hexadecimal values, but only allowed the values of zero through nine rather than the full 16 values that were possible (as shown in Table 4-5). The reason for using this data structure has largely disappeared in computer systems, but it is still a viable and useful method of handling data in digital electronics and one that you should keep in your ‘‘hip pocket’’ when you design circuits.

The original reason for using the BCD data format in computer programming was its elimination of the need to add code to the program to convert a binary or hex number into decimal. The code storage required for the conversion was expensive and the processors were nowhere near as possible as what is available today. Using decimal values was actually an optimal way of processing data in these old systems.

The lasting legacy of this is the number of standard chips that can process BCD values just as easily as other standard chips can process hexadecimal values and will allow you to design circuitry that works with decimal values just as easily as if you were working with hex values.

While this is getting a bit ahead of things, I want to give the example of designing a delay that holds back a signal for 100 seconds. Using traditional binary logic, which only works with bits that are a power of two, you would have to design a circuit that compares a counter value and indicates when the

value ‘‘100’’ was reached and reset itself. When using digital electronic chips that are designed for BCD values, the comparator function is not required, as each BCD digit cannot be greater than ‘‘9’’ and, cascaded together, they can only count to a maximum value of ‘‘99’’ to ‘‘00’’.

This may seem like a trivial example, but you will find a number of cases like this one where you will have to create circuits that work on base 10 data and by using chips which are designed for BCD values, the complexity of your work will be greatly reduced.

Going back to Table 4-5, the production of the ‘‘invalid’’ indication is

worthy of some discussion as it provides a good example of how gate optimization is not always as straightforward as you might expect.

In most BCD chips, if the value of 10 or more is passed in the binary bits, then the value is converted to zero and a carry indication is output. Using the tools presented in Chapter 2, you should be able to derive the sum of products formula for the positive active ‘‘invalid’’ indicator as:

and using the conversion formulas of Chapter 2, you would simplify the ‘‘invalid’’ formula above to:

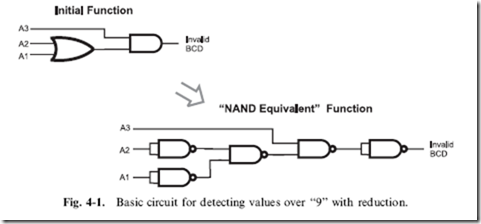
Figure 4-1 shows the AND/OR gates for this function along with the ‘‘NAND equivalent’’ function beneath it. The NAND equivalent was chosen by assuming that the function would be implemented in TTL. While this circuit looks a bit complex, if you follow it through, you will find that it provides the same function as the AND/OR combination above it.

It will probably surprise you to find out that this circuit is not optimal by any measurement: you can do better in terms of the number of gates, the time

it takes a signal to pass through the gates and in providing a constantly timed output. The circuit at the bottom half of Fig. 4-1 will respond in two gate delays if A3 changes and in four gate delays if A2 changes. For many circuits, this is not a problem, but when you are working with high-performance designs, a variable output delay can result in the application not working correctly and being almost impossible to debug.

A much better approach to optimizing the circuit is to work at converting it to the basic gate used by the technology that you are working with and then optimizing this. Going back to the original ‘‘Invalid’’ equation:

I can convert the OR to a NAND, by inverting its two parameters (according to De Morgan’s theorem), ending up with:

It is probably astounding to see that the function provided by the mess of NAND gates in Fig. 4-1 can be reduced to the three simple gates required by the formula above. Along with reducing the number of gates, you should also notice that the maximum number of gate delays is two, regardless of which bit changes.

Looking at the NAND circuits in both diagrams, you are probably  at a loss as to how you could reduce the NAND circuit in Fig. 4-1 to the three

gates of the optimized circuit. Personally, I would be surprised if you could; when I look at the two circuits, they look like they provide completely different functions.

What I want to leave you with is an example of how looking at a logic function from different perspectives can result in radically different circuits

with surprisingly different parameters. In the first case, I reduced three gates to two, to end up with six NAND gates, while in the second, I avoided reducing the basic function and converted it directly to a much more efficient three NAND gate circuit.

In going through this exercise to produce the ‘‘invalid’’ output for BCD, I hope that you can apply this knowledge for creating circuits that work with different base systems than just a power of two. In some cases, you may have to work with numbers that are base 9 or 13 and using the example here, you should have some idea of how to keep the values within certain ‘‘bounds’’.

Gray Codes

I hope I have convinced you of the usefulness of using Gray codes for inputs when you are illustrating how digital electronic logic functions respond to inputs. I must point out, however, that Gray codes were originally created for a much different function – they were designed for use in position sensors as the single changing bit allowed hardware to be designed to respond to a single changing bit and not the potentially several bits of a binary sequence. By only changing one bit at a time, absolutely precise positioning of marking sensors (causing all changing bits being sensed at the exact same instant) was not required.

Gray codes were invented by Frank Gray of Bell Labs in the mid 1950s and has a ‘‘hamming value’’ of 1. The hamming value is the number of bits that change between one value and the next. A four bit binary number can have all four bits change as it increments or decrements; a Gray code never has more than one bit change during incrementing or decrementing operations.

Chances are, you would not have any trouble coming up with a two bit Gray code (b’00’, b’01’, b’11’ and b’10’) and in a pinch, you would be able to come up with a three bit Gray code (b’000’, b’001’, b’011’, b’010’, b’110’, b’111’, b’101’ and b’100’). I suspect that if you were given the task of coming up with any more bits than this, you would be stumped.

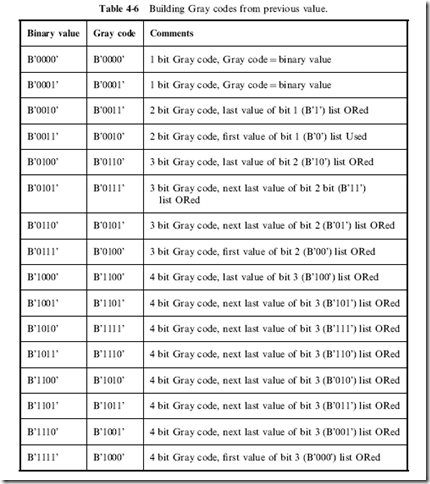
In trying to come up with a way of explaining how Gray codes worked, I noticed that when a new most significant bit was set, the previous values were ORed with this bit, but written out in reverse order. In some texts, this property is recognized by calling Gray codes a binary reflected code. Looking at Table 4-6, you can see that I created a four bit

Gray code by taking the eight values of the three bit code, reversing them and setting bit 3.

This could be written out as a computer program algorithm as:

This code demonstrates how Gray codes are produced, but is not the optimal method for producing Gray codes (it is actually an ‘‘order n2’’ algorithm, which means that every time the number of bits is doubled, the amount of time required to produce the values is quadrupled). Along with this, it is not easy to create digital logic hardware that will create these codes.

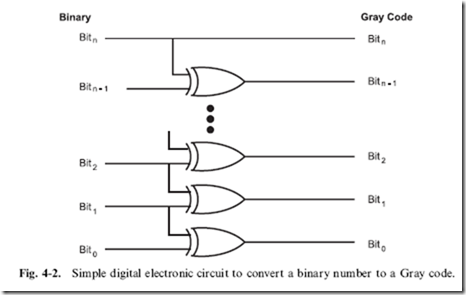
Fortunately, individual binary codes can be converted to Gray codes using the circuit shown in Fig. 4-2, which simply implements the formula:

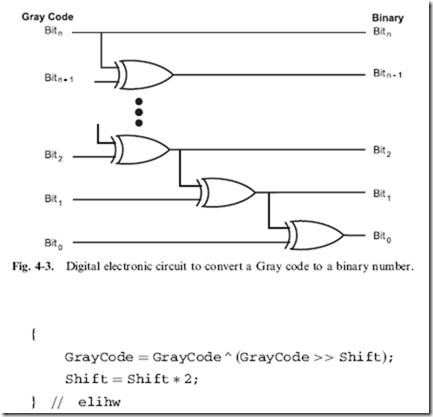
Going the other way (from Gray code to binary) is a bit more complex and while it uses n – 1 (where ‘‘n’’ is the number of bits) XOR gates, like converting binary codes to Gray codes, the output of each XOR gate is required as an input to the next least significant bit, as shown in Fig. 4-3. The output of the circuit is not correct until the most significant bit has passed through each of the XOR gates to the least significant bit.To perform the data conversion a simple formula cannot be used. Instead  the following algorithm is required:

I find it very difficult to explain exactly how this code works, except to say that with each iteration of the while loop, the ‘‘Gray code’’ value gets shifted down more and more to move the most significant bits into position for XORing with the less significant bits. To convince yourself that the algorithm works, you might want to perform a ‘‘thought experiment’’ on it and list the changing value of ‘‘Gray code’’ as I have done in Table 4-7.

In this chapter, more than anywhere else in the book, I have used sample computer programs to show how different values can be produced. This is a somewhat different approach to explaining how multi-bit binary data conversions are implemented and one that takes advantage of the ubiquity of the personal computer and the ability of most technical students to perform even rudimentary programming.

Using computer code to help demonstrate how the conversions are done should also give you another method for processing binary values as well as of testing formulas and optimizations. I always find it useful to have a number of different ways to solve a problem, or test a potential solution,

Table 4-7 Working through the shifting values of the Gray code convention algorithm.

Initial bit values	Shift ¼ 1 bit values	Shift ¼ 2 bit values	Shift ¼ 4 bit values
B7	B7	B7	B7
B6	B6 ^ B7	B6 ^ B7	B6 ^ B7
B5	B5 ^ B6	B5 ^ B6 ^ B7	B5 ^ B6 ^ B7
B4	B4 ^ B5	B4 ^ B5 ^ B6 ^ B7	B4 ^ B5 ^ B6 ^ B7
B3	B3 ^ B4	B3 ^ B4 ^ B5 ^ B6	B3 ^ B4 ^ B5 ^ B6 ^ B7
B2	B2 ^ B3	B2 ^ B3 ^ B4 ^ B5	B2 ^ B3 ^ B4 ^ B5 ^ B6 ^ B7
B1	B1 ^ B2	B1 ^ B2 ^ B3 ^ B4	B1 ^ B2 ^ B3 ^ B4 ^ B5 ^ B6 ^ B7
B0	B0 ^ B1	B0 ^ B1 ^ B2 ^ B3	B0 ^ B1 ^ B2 ^ B3 ^ B4 ^ B5 ^ B6 ^ B7

and I suggest that along with the various tools and computer algorithms presented in this book that you try to come up with methods for yourself that will help you design and test digital electronic circuits more efficiently.

Quiz

1. If you had a number system that was base 5, the most significant value in a digit would be:

(a)	6
(b)	10
(c)	4
(d)	5

2. The eight bit binary equivalent to decimal 47 is: (a) 0010 1111

(b) B’0010 1111’

(c) 101111

(d) 1011 11

3. The third most significant digit in the decimal number ‘‘1234’’ is:

(a) The hundreds column

(b) 3

(c) 1

(d) No digit can be the third most significant

4. To verbally tell somebody the hex number value 0x04AC you would say:

(a) ‘‘Four-Able-Charlie’’

(b) ‘‘Hexadecimal Four-Eh-See’’

(c) ‘‘Hexadecimal Four-Apple-Charlie’’

(d) ‘‘Hexadecimal Four-Able-Charlie’’

5. The decimal number ‘‘123’’ in hexadecimal is:

(a) 0x0123

(b) B’0111 1011’

(c) 7B

(d) 0x07B

6. The four bit hexadecimal number 0x01234 expressed in decimal is:

(a) 1,234

(b) 4,660

(c) B’0001 0010 0011 0100’

(d) 0x04D2

7. Binary coded decimal is defined as:

(a) Ten bits providing ten different values

(b) Four bits providing ten numeric values and six control codes

(c) Four bits providing ten numeric values

(d) Five bits with each bit providing two values for a total of 10

8. BCD should:

(a) Never be used

(b) Used with circuits that operate with base 10 numbers

(c) Only be used when you’ve run out of binary chips

(d) Used when values are not expected to exceed 9

9. B’0110’ in binary, using the formula Gray code ¼ binary ^ (binary » 1) can be converted to the Gray code:

(a) B’1010’

(b) B’0110’

(c) B’0101’

(d) B’0111’

10. The Gray code B’0010’ corresponds to the binary value: (a) B’0011’

(b) Unknown because more data is required (c) B’1101’

(d) B’0010’