Work, Heat, & Reversible Change
State Functions & Path Functions
Work, W , and heat, Q, are obviously very important in thermodynamics, playing a central role in the First Law [Equation (7.3)]. They are also unique, in being the only thermodynamic quantities that are not also state functions. By the latter, we mean quantities such as U(T, V ) that depend only on the thermodynamic state. In contrast, values for work and heat can only be assigned to thermodynamic processes (changes of state)—never to individual states themselves.
⊳⊳⊳ To Ponder… One imagines the stereotypical Holly- wood agent, promoting his or her clients as “having heat.” Thermodynamically speaking, this is nonsense; one can “release heat” or “absorb heat,” but not “have heat.” What one “has”—though admittedly a lot less catchy—is internal energy.
For a change from initial state A to final state B, the generic state function change, ΔX , depends only on A and B themselves [as per Equation (7.1)], and not on the specific path taken through “state space” to get from A to B (as in Figure 7.2). The opposite is true for the non-state-function quantities, W and Q. In other words, it is not only the path endpoints, A and B, that determine W and Q, but also all of the states in between. Such quantities are called path functions, to emphasize this path dependence.
⊳⊳⊳Helpful Hint: To use a driving analogy, “elevation” is a state function; it depends only on where you are, not on where you’ve been. On the other hand, “mileage” is a path function—nonzero for a round trip, and otherwise dependent on your past travel history.
⊳⊳⊳ Helpful Hint: For equations describing thermodynamic change, every term must have one ‘Δ’ in it. The only exceptions are for the path functions, W and Q, as in Equation (7.3). Also, remember that ‘Δ’ expressions are always computed as “final minus initial” [Equation (7.1)]—not the other way around.
⊳⊳⊳ Don’t Try It !! Don’t ever combine ‘ΔX ’ expressions and ‘X ’ expressions (i.e., with no ‘Δ’) in the same equation! This is the third most common error made by stu- dents, after the “liter/cubic meter” error of Section 3.2, and the “ideal gas” error of Section 4.4. Specific examples with correct usage are listed in the Helpful Hint on p. 74.
Definition of Work
We all have some intuitive notions of what “work” and “heat” are. More mathematically, we learn from Equation (7.3) that both W and Q are extensive quantities with units of energy. But these are mere descriptions, not quantitative, scientific definitions. Fortunately, physics already provides a definition of mechanical work—one that is best expressed in differential form.
Consider an infinitesimal thermodynamic change—i.e., one in which the initial state A and final state B become arbitrarily close. Thus, (Pf , Vf ) ≈ (Pi, Vi ), or (Pf , Vf ) = (Pi + dP, Vi + dV ), where dP and dV are differentials. For an infinitesimal change, ΔP → dP and ΔV → dV ; the same is also true for all other state function quantities—i.e., ΔX → dX .
where Fsur is the opposing force, and dz is the infinitesimal change in the object’s position.
In thermodynamic terms, the “opposing” force is that imparted by the surroundings, and the macroscopic object is the (movable) dividing wall. These ideas are conveniently encapsulated in the piston-cylinder apparatus of Figure 8.1.
From Equation (4.4), pressure can be obtained from force, by dividing by the area of the movable wall. Likewise, infinitesimal distance becomes infinitesimal volume when multiplied by the wall area, so that
Figure 8.1 Expansion work for piston-cylinder apparatus. The “system” is the gas inside the cylinder. The piston itself serves as the movable dividing wall; as part of the surroundings, it also provides the opposing force, Fsur (and the surroundings pressure, Psur). Expansion is in the vertical direction. The resultant infinitesimal work [Eqs. (8.2) and (8.3)] is negative; work is done by the system on the surroundings.
From Equation (8.4), there are two conditions that are absolutely required of any thermodynamic process, in order for it to exhibit nonzero work. These are:
1. a change in the system volume, V .
2. a nonzero surroundings pressure, Psur, against which the expansion takes place.
Both conditions are necessary. Without Condition 1, there is no macroscopic motion, and therefore no work. Without Condition 2, there is free expansion (see Section 16.2), but again, no work.
⊳⊳⊳Helpful Hint: Equation 8.4 is a definition, and as such
may always be relied upon. You will encounter many other,
conditional expressions for W (Sections 8.5 and 16.3) that you may also use—but which only apply under special circumstances. When in doubt, use the definition; it is always correct.
Definition of Heat
Heat will be treated a little differently than the other thermodynamic quantities considered thus far. Rather than describe heat at the macroscopic scale and define it at the molecular scale, we will do exactly the opposite.
Qualitatively, we already understand what heat is at the molecular scale: it is the transfer of molecular kinetic energy across a diathermic wall. This is merely a description, however, not a definition. Whereas it might be possible to actually define Q at the molecular scale, we prefer to define it at the macroscopic scale, directly from the First Law:
Thus, heat is “whatever is left over” in a thermodynamic change, when the work is subtracted from the change in the internal energy.
Since ΔU and W are well defined for any thermodynamic process, so is Q. There is absolutely nothing wrong with this definition—it satisfies the criterion of Definition 1.1 (p. 4) perfectly well. Moreover, from a practical standpoint, Equation (8.5) conveys the usual procedure that you should follow, when asked to compute Q in problems.
Reversible & Irreversible Change
Why is the thermodynamic path taken to be Psur(V ) rather than P(V )? This is because P itself is not necessarily well defined throughout the entire process, since the system may venture far from equilibrium at intermediate times. We know that at least the path endpoints, A and B, are necessarily both equilibrium states—but in between, it could well be another story.
On the other hand, we do presume that the surroundings are always in equilibrium throughout the thermodynamic change—so that Psur is always well defined. An extremely important consequence is that the work [Equation (8.4)] is also always well defined, even for irreversible processes (see below).
⊳⊳⊳ To Ponder… The above underscores another important difference between system and surroundings—and another reason why the “total system” (Section 7.1) and “subsystems” (Section 4.3) pictures are not the same.
We distinguish two types of thermodynamic change:
reversible The system is in equilibrium at every step along the path from A to B, with P = Psur throughout.
irreversible The system is far from equilibrium for at least part of the path from A to B.
Reversible change is an idealization—if a system were truly in equilibrium (Definition 4.1, p. 26), its thermodynamic state would never change! In practice, what “reversible” really means is that external factors change very slowly—so that the system can gently readjust itself, incrementally through- out the process. As a consequence, the system never gets very far away from the equation of state.
In contrast, irreversible change occurs after a sudden external change has pushed the system far from equilibrium. The system then undergoes an automatic or “spontaneous” thermodynamic change, until a new equilibrium state is reached (see Section 12.3).
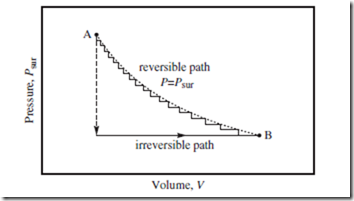
Figure 8.2 Reversible and irreversible paths. Two isothermal paths—one reversible and one irreversible—to get from A to B. The dotted curve represents the true reversible path, an isotherm. The vertical dashed line and horizontal solid line represent the irreversible path. See main text for further discussion.
Figure 8.2 depicts two different isothermal (constant T) paths to get from A to B—one a reversible path, the other an irreversible path. The reversible path is an isotherm—i.e., a contour of the T(P, V ) equation of state (treating T as the dependent variable; see box on p. 24). In reality, a nearly reversible path might look more like the staggered solid curve— obtained when Psur is reduced slowly, so that P ≈ Psur throughout. In contrast, when Psur is suddenly reduced (vertical dashed line), a spontaneous change ensues (horizontal solid line) until equilibrium is again restored at B. This is the irreversible path.
Your primary textbook most likely discusses work as being “the area under the path.” The two paths indicated in Figure 8.2 clearly have different W ) W values. Note that the reversible path generates more work (larger | | than does the irreversible path. This is always the case for a true ΔV > 0 expansion; of all physically realizable paths from A to B, the reversible path yields maximum work.
Why should this be the case? To expand a gas, one must first ease up on Psur, and then allow the system to increase V on its own (thereby restoring equilibrium). Hence, all real isothermal expansion paths lie below the reversible path indicated in Figure 8.2. To compress a gas, one first increases Psur, and then allows V to decrease. Thus, all real compression paths lie above the reversible path in Figure 8.2.
A Gas Expansion Example
We actually did this once before, in Fig. 7.2—now seen to be a reversible isobaric expansion.
There is a bewildering variety of different kinds of gas expansions. There are reversible and irreversible expansions, for gases that are either ideal or non-ideal. Some expansions are isothermal (constant T); others are iso- baric (constant Psur). There are also free (W = 0) and adiabatic (Q = 0) gas expansions.
In Section 16.3, we offer a comprehensive compendium. Here, we successively narrow the focus down to one classic example: the reversible isothermal expansion of an ideal gas. Refer to Figures 8.1 and 8.2.
Reversible expansion: For the special case of a reversible gas expansion, Psur = P at every point along the path from A to B. This means that we can replace the vertical axis in Figure 8.2 with P. The path Psur(V ) thus becomes the reversible path, P(V ). Moreover, because the system is in equilibrium throughout, we know that the reversible path lies on the equation of state. Consequently, the temperature is not arbitrary, but is determined from the T(P, V ) equation of state [T(V ) = T(P(V ), V )].
Reversible expansion of ideal gas: Let us further specialize, by assuming that our reversible expansion applies to an ideal gas. This means that the reversible path P(V ) in Equation (8.6) can be related to T via the ideal gas equation of state, P(V ) = nRT∕V . The work, in turn, becomes W = − ∫ nRT(1∕V ) dV .
Reversible isothermal expansion of ideal gas: Only by specifying that the reversible ideal gas expansion path is isothermal can we treat T as a con- stant. We thus obtain W = −nRT∫ (1∕V ) dV , or