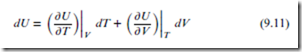Partial Derivative Quantities
In the previous chapters (and in Chapter 16), we have explored essentially all there is to know about T, P, V , U, W , and Q, on their own. Accordingly, in this chapter, we introduce a host of new thermodynamic quantities. Instead of delving down to the molecular scale and applying statistical mechanics—as was done previously, e.g., for U—the new quantities are derived directly at the macroscopic scale, from previously defined quantities. This is perfectly legitimate, since It’s OK to be Lazy; in fact, we have already used this strategy in our definition of heat [Equation (8.5)].
Most of the new quantities are defined as mathematical derivatives of other state function quantities—exploiting the fact that the latter are, in fact, functions of the independent thermodynamic variables. Of course, there are two variables, rather than just one—necessitating the use of partial derivatives, rather than ordinary derivatives, and otherwise making things more difficult and confusing.
Internal Energy & Heat Capacity at Constant Volume
In Section 8.5, we discussed the reversible isothermal expansion of an ideal gas. How could such an experiment be realized in practice? One simple sce- nario would be to imagine dunking the entire piston-cylinder apparatus of Figure 8.1 into a very large heat bath, represented schematically as the surroundings in Figure 7.1.
While the piston is slowly moved, and the system thus reversibly expanded, heat flows from the bath to the system. This compensates for the system internal energy that is being lost in the form of work. How- ever, because energy is extensive and temperature intensive, the heat loss of the surroundings results in only a negligible reduction in Tsur—which is therefore effectively constant. Finally, since the system and surroundings are in thermal equilibrium with each other throughout the expansion pro- cess, T = Tsur is also constant.
The above scenario plays out the way it does because of something called the heat capacity—essentially, the ratio between heat and tempera- ture change. You have no doubt known about heat capacity for some time, but probably not as a true thermodynamic state function. Our goal in this section is to define one such heat capacity quantity. First though, we must consider a new type of thermodynamic change.
Instead of changing V while keeping T constant (i.e., as in isothermal expansion), consider changing T while keeping V constant. Since the volume does not change, there is no work; all internal energy change is thus due to heat alone:
ΔU = Q [const V ] (9.1)
We can therefore measure Q experimentally simply by measuring ΔU, or vice-versa—but only under constant volume conditions. For an ideal gas, moreover, we can obtain both Q and ΔU simply by measuring ΔT and the amount of substance. This is the basis of calorimetry:
Implicit in the partial derivative expression of Equation (9.3) is the assumption that T and V are the two independent variables—with T varying, and V fixed. Note that CV = CV (T, V ) is itself a state function quantity. In the general case, it depends on both variables, T and V . For the ideal gas special case, however, we see from the differential form of Equation (9.2) [i.e., dU = dQ = (3∕2)nR dT] that CV is constant:
Note that CV is extensive—which is why it is large for a large heat bath, leading to negligible ΔTsur for the example discussed at the start of this section.
Enthalpy & Heat Capacity at Constant Pressure
In calorimetry—and in many other contexts, too—we find that T and V are a natural choice of independent variables to use with U. In principle of course, any other variable pair could also be used, but there is a definite preference for thinking of U = U(T, V ).
One very nice property of Equation (9.1) is that it effectively turns a path function (Q) into a state function (ΔU). Path functions—particularly W — can be difficult to measure in real applications; thus a great simplification results when W is known in advance to be zero, as in the case of bomb calorimetry.
On the other hand, most real processes do not occur under constant volume conditions, but rather, under constant pressure conditions. Unfortunately, there is no special relationship between ΔU and Q at constant P.
We therefore seek a new thermodynamic quantity, X , such that:
• X is an extensive state function with dimensions of energy.
• X is closely related to U.
• The natural variables for X are T and P.
• ΔX = Q at constant P.
Such a quantity, should it exist,would be very useful in practice—because for any constant P process, it would avoid entirely the need to worry about work. Such a quantity does indeed exist; it is called the enthalpy.
In practical terms, CP is generally more useful than CV ; for example, CP is what is usually meant when the term “heat capacity” is used by itself (i.e., with no additional qualifier). That said, the relation between the two heat capacities has important thermodynamic relevance. The heat capacity
ratio, = CP∕CV , plays a key role in reversible adiabatic change (is also called the adiabat coefficient). For the ideal gas, is constant; however, its value depends on whether or not point particles are presumed (see Sections 13.1 and 16.2).
So what is enthalpy, really? Enthalpy is by no means a true energy, and is therefore far less fundamentally important than the internal energy. Probably the best way to think of enthalpy is simply as a practical tool—an energy-like quantity, better suited to constant P processes than is U itself. Working with H at constant P, Q effectively becomes a state function, and W can be ignored altogether. This is certainly handy, however…we would probably never have a need for enthalpy, were it not for the fact that we happen to like performing experiments at constant pressure.
Other Partial Derivative Quantities
According to the rules of calculus, the total differential for the state function U(T, V ) is given by:
The first partial derivative above is CV . The second partial derivative is also a useful quantity; it has dimensions of pressure, and is called the internal pressure, denoted ‘T ’:
The two partial derivatives in Equation (9.13) measure how V changes with respect to T and to P, respectively. These are thus quite useful in engineering, in the characterization of materials—but only after they are first converted into intensive quantities, via division by V .
In this manner, we obtain the following “relative expansion quantities”:
Note the minus sign in Equation (9.15); this is introduced so that T itself is positive—since V always decreases, when P increases at constant T.
Why stop now? Why not continue to differentiate everything in sight, thereby creating a zillion new state function quantities? We could certainly do this, but there would be very little point. In practice, new thermodynamic quantities are introduced for one of three reasons:
1. They are theoretically meaningful.
2. They are experimentally useful.
3. They connect other quantities that we care about, through partial derivative relations.
Reason 3 will become a bit clearer in the next section.
Partial Derivatives & Differentials
We have made many references to “differential forms,” “total differentials,” and “partial derivatives.” These are the building blocks of multivariable calculus, and also, useful tools for understanding thermodynamic change. Accordingly, in this section we explore some of the underlying mathematics in greater detail.
⊳⊳⊳ To Ponder… Warning! As with Chapter 6, the material in this section may be somewhat advanced and/or not so immediately relevant for some students. Accordingly, some readers may prefer to proceed directly to Chapter 10.
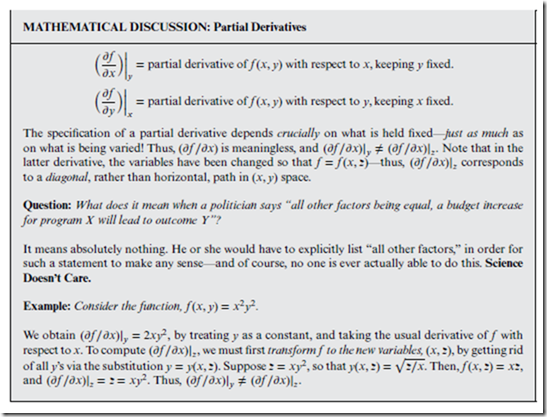
Consider a generic mathematical function f (x, y), in the two independent variables, x and y. We understand the basic idea that the “derivative” represents how f changes with respect to the independent variable— but since there are two of these instead of one, there are two independent ways in which the variables can change, and therefore two partial derivatives.
⊳⊳⊳ To Ponder… In fact, there are many ways that the variables can change—corresponding to many diagonal paths in the (x, y) “state space” (one such path is indicated in the marginal figure on this page)—and thus, there are many different partial derivatives.