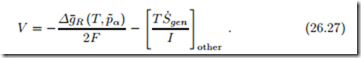Mass Transfer Losses
The pressure considered in the Nernst equation above are the pressures at which the inflows are supplied, and the outflows are removed, that is the pressures in the transport channels. The transport of reactants and products through the porous gas diffusion layers leads to friction losses, and thus generation of entropy as discussed in Sec. 9.7. Entropy generation and over- potential associated with this loss will be determined next.
The flow through the porous medium can be described by Darcy’s law (9.30) which we can write for mole flows as
where flow goes from pα,1 to pα,2; K is an overall transport parameter.
For ideal gases, the corresponding entropy generation rate (9.29) can be written in the equivalent forms3
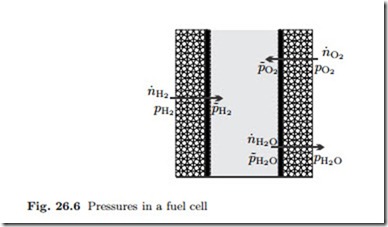
The relevant mole flows and pressures for a hydrogen fuel cell are depicted in Fig. 26.6, where pα denotes the pressures in the gas channels, and p˜α denotes the pressures at the catalyst layers. Note that hydrogen and oxygen flow from the channels to the catalyst layer, while water flows in the opposite direction. The mole flows are related to current as
For compact notation we used the abbreviation Iα = 2F Kαpα/ |γα| for the so-called limiting currents. Note that all pressures in these are taken in the supply channels. The different forms of the expressions are due the fact that H2 and O2 are entering the device, while the water leaves; all three expressions are positive.
In the fuel cell literature, one sometimes finds these contributions to loss, or overpotential, subsumed into just one expression of the form
Here, the last term refers to other contributions to entropy generation which will be discussed below.
In acidic fuel cells, water is produced at the cathode, and must be removed. In low temperature fuel cells the produced water is liquid, and might clog the pores of the gas diffusion layer, and even the gas channels. This reduces the transport parameter K and the limiting current Ilimit. The air flow that provides the oxygen must be dry enough, so that the product water can evaporate into the exhaust. The use of excess air increases the water intake, and also guarantees sufficient oxygen pressures everywhere (see Nernst equation).
It is worth noting that the Nernst equation and the entropy generation terms for transport can be combined to give the fuel cell potential as4
This form of the equation shows that it is really the pressures p˜α at the catalyst layers that are important. These however cannot be controlled, rather they depend on the pressures pα in the gas channels and the current I as expressed in (26.23). This dependence is explicit in the form (26.26), which therefore must be used.