Thermodynamic States, Variables & Quantities
Thermodynamic Variables & Quantities
As discussed in Chapter 2, thermodynamics is able to reduce all of the molecular-scale complexity of macroscopic systems down to just a few thermodynamic variables. These are:
• temperature, T
• pressure, P
• volume, V
• number of particles, N
Remarkably, these four variables alone determine everything there is to know about the system at the macroscopic scale. In other words, from know- If you learn nothing else froming the values of the four thermodynamic variables, the value of any other macroscopic quantity may be predicted with perfect precision, without the this chapter, let it be this.
need to conduct an actual laboratory measurement. Although there are some caveats, this is an amazing fact—and the reason that we can regard thermodynamics as a being a true law, rather than a mere model. More technically, we say that thermodynamics is macroscopically complete.
On to the caveats. First, in addition to the four thermodynamic variables, knowledge of the particular substance of which the system is composed is also required, in order to make specific macroscopic predictions. Second, thermodynamics does not tell us everything there is to know about the individual molecules that make up the system. As a predictive theory, thermo- dynamics is decidedly incomplete at the molecular scale. Still, molecular information is not actually necessary, in order to understand with perfect precision what is happening at the macroscopic scale.
Next, we clarify some terminology. By thermodynamic system, we simply mean “a macroscopic amount of stuff ” (i.e., bulk matter). Macroscopic, in turn, means that the number of molecules or particles is on the order of Avogadro’s number,
A thermodynamic quantity is any macroscopic property of the system that can be measured as a number; this includes the four thermodynamic variables, among many others. To specify a quantity with perfect precision means “to any desired accuracy”—i.e., to any number of significant digits.
the quantity is “well defined.” We also take a substance (or pure substance) to be a thermodynamic system whose constituent particles are all of the same kind. This assumption is presumed throughout this book.
For a pure substance, the most fundamental thermodynamic quantity imaginable is the amount of substance—i.e., how much “stuff ” there is. There are two ways to reckon this. The molecular-scale quantity is N, the number of particles (molecules). There is also a macroscopic measure of the amount of substance, the so-called number of moles, n, defined as
There is no fundamental difference between N and n; the distinction is merely one of scale. In statistical mechanics and physics, N is usually preferred, whereas in thermodynamics and chemistry, n is typically used. Engineers eschew both quantities, preferring to work with the system mass, Nm = nM, where m is the mass per particle, and M is the mass per mole (molar mass). In any case, we have now defined our first thermodynamic quantity, and we did so by following Einstein’s advice—i.e., by counting.
More on Thermodynamic Quantities
There are many thermodynamic quantities that can be defined or measured. and with perfect precision, no We usually denote these quantities using capital letters—with ‘X ’ representing a generic choice.
Thermodynamic quantities can be usefully divided into two basic types:
extensive vary proportionally with n.
intensive independent of n.
Note that any extensive quantity can be converted into an intensive quantity, simply by dividing by n. The resultant molar quantity receives an ‘m’subscript.
Any quantity in science can be characterized with both a number and a unit. Since thermodynamics describes macroscopic systems, we generally use macroscopic units—almost always Syste`me International (SI) units. Note that thermodynamic quantities always describe the whole system, rather than individual particles. This is true even for molecular-scale thermodynamic quantities, such as the per-particle average, (X ∕N).
Although SI units are very standard—meters (m) for length, Joules (J) for energy, Pascals (Pa) for pressure, etc.—it is still possible to get into trouble. For students of thermodynamics, the most common error by far is to take the liter (L) as the SI unit of volume.
The correct SI unit of volume is the cubic meter (m3),which is exactly equal to 1000 liters. Students often make the “liter/cubic meter” error when computing energy as pressure times volume. In SI units, we have
1J=1 Pa m3, not 1J=1 Pa L
⊳⊳⊳Helpful Hint: Because the “liter/cubic meter” error is so common, when solving problems, you should always be on the lookout for results that are either 1000 times larger or smaller than they should be.
Thermodynamic & Molecular States
When a measurement or scientific theory provides a complete description of a physical system, we say that the system’s state is determined. Conversely, knowledge of the system state suffices to predict the value of any desired quantity. From Section 3.1, we learn that the four thermodynamic variables (T, P, V , N) collectively specify the macroscopic or thermodynamic state of a thermodynamic system. Insofar as thermodynamics is concerned, all systems of a given molecular type, with the same values for these four variables, occupy the same thermodynamic state. Since these systems must exhibit the same value for any thermodynamic quantity, there is simply no macroscopic way to distinguish them.
According to the laws of physics, however, the system can also be described in terms of its molecular state. For a single molecule, this state is determined from the following:
• particle position, (x, y, z)
• particle velocity, (vx, vy, vz)
• internal structure
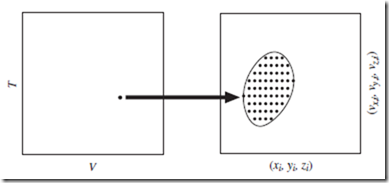
Figure 3.1 One-to-many relationship between thermodynamic states and molecular states. For a given thermodynamic state of the system [the point (T , V ) in the left plot; don’t worry about P and N], there are many possible molecular states (the set of points in the right plot), amongst which thermodynamics cannot distinguish.
Although real molecules possess internal structure, in thermodynamics, we often treat molecules as if they were “point particles” (see Section 5.3)— in which case, only the position and velocity are required to specify the particle’s state.
For an entire macroscopic system, the molecular state is defined to be the collection of single-molecule states for the constituent molecules, taken together. Specifying the molecular state of the whole system thus requires at least 6N coordinates—the three position components, (xi, yi, zi ), plus the three velocity components, (vx,i, vy,i, vz,i ), for each molecule, i, where the label i is an integer with 1 ≤ i ≤ N.
As discussed, knowing the thermodynamic state of a system does not provide specific information about individual molecules. Since most of these molecular details remain macroscopically hidden, there is a very large number of possible molecular states that correspond to any given thermo- dynamic state—i.e., that are consistent with what is known macroscopically about the system. This one-to-many relationship between thermodynamic and molecular states, indicated in Figure 3.1, is extremely important.