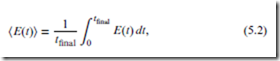Molecular Energy, Internal Energy,& Temperature
This chapter is about energy, the most important quantity in all of science. Our main goal is to define the internal energy—a new thermodynamic quantity, denoted ‘U’. Though internal energy is macroscopic, the definition requires an understanding of energy at the molecular scale, which we accordingly also consider. Along the way, we will come to better understand how molecules interact, and what qualitative effect this interaction has on the macroscopic behavior of the system (e.g., on the equation of state).
We also define the temperature, denoted ‘T’.
Energy at the Molecular Scale
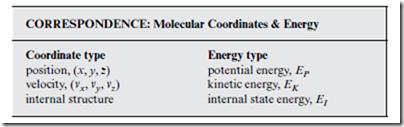
From the laws of physics, we learn that there are two kinds of energy: potential energy and kinetic energy. At the molecular scale, it is convenient to imagine a third kind of energy possessed by individual molecules, which we call the internal state energy. Each type of energy is associated with a different type of molecular coordinate.
When the subscript i is applied to the quantities in the box above, this refers to the specific molecule i. Thus, EK,i is the kinetic energy associated with the translational (center-of-mass) motion of molecule i. “Potential energy” refers to the intermolecular interactions among molecules. Strictly speaking, EP depends on the relative (to other molecules) molecular positions, rather than on the absolute (center-of-mass) molecular positions, (xi , yi , zi). However, this distinction does not matter for our purposes. Finally, EI represents the energy associated with intramolecular interac- tions. For most thermodynamics applications, EI,i can be regarded as the chemical energy stored in molecule i—if indeed, it need even be regarded at all.
According to the laws of physics (specifically conservation of energy), E remains constant over time, provided that the system is “isolated” (see Section 7.1). This is not the case for most thermodynamic systems, which are usually in thermal and/or mechanical contact with their surroundings. Consequently, energy can flow freely in and out of the system over time, and so E is not constant. This is true even when the system is in complete thermodynamic (i.e., both mechanical and thermal) equilibrium.
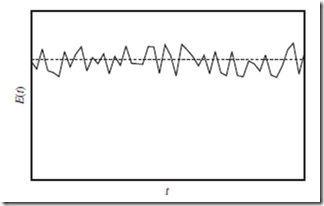
Figure 5.1 Molecular state energy as a function of time. Energy of the molecular state of the whole system, E, as a function of time, t (solid curve), for a sys- tem in thermodynamic equilibrium. As indicated, E(t) itself is not constant, but tends to fluctuate around its time-averaged value, ⟨E(t)⟩—indicated by the hori- zontal dashed line. This constant value is (essentially) the internal energy, U.
Internal Energy
Because E can change over time even when the thermodynamic state does not, this means that E itself cannot be a thermodynamic quantity, according to Definition 4.1 (p. 26). So how can we define a meaningful thermodynamic energy quantity? This is where the idea of statistical averaging comes in—specifically, time averaging (Section 2.3).
A plot of the molecular state energy, E, as a function of time, t, for a macroscopic system in thermodynamic equilibrium, would look something like Figure 5.1. Note that E(t) oscillates very quickly, but never gets far from the time-averaged value. These oscillations are called fluctuations. According to statistical mechanics, fluctuations quickly cancel out when averaged over macroscopic time scales, and can therefore be ignored—provided that the system is both large (N → ∞), and in equilibrium.
In practice, the time-averaged quantity,
is much more useful than E itself. Moreover, for a system in equilibrium, E(t) is constant over time, and may therefore be regarded as a true thermodynamic quantity. We take this quantity to be the internal energy (after subtracting the internal state energy).
Definition 5.1 For a system in equilibrium, the internal energy, denoted ‘U’, is defined to be the time average of the molecular state potential-plus-kinetic energy:
Note from Equation (5.3) that U can be obtained from the time averages of the individual molecule potential and kinetic energies, Note also the absence of EI,i. The internal state energy is not included in the definition of U, because it plays no direct role in many “traditional” thermodynamic processes such as gas expansions.
The internal energy includes, say, the energy available to do work, but does not include, say, the translational kinetic energy arising from movement of the whole thermodynamic system (i.e., the experimental apparatus) through space.
Sections 5.3 and 5.4, respectively, will discuss potential and kinetic energy in more detail.
Intermolecular Interactions & the Kinetic Model
As discussed in Section 5.2, internal state energy is ignored in the calculation of U. From a molecular viewpoint, this is equivalent to making the assumption of point particles. As per the discussion in Section 3.3, point particles have no internal structure, and therefore no internal state energy. Very often this is a good assumption, thermodynamically speaking, pro- vided that the actual internal state does not change.
Note that some authors refer to point particle systems as “monoatomic” systems—e.g., argon gas. This is reasonable nomenclature, but only to a point; even monoatomic systems have internal atomic structure. Conversely, even non-monoatomic systems, such as diatomic nitrogen, can in some ways be treated as point particle systems. We therefore prefer the “point particle” terminology.
Another commonly made assumption in thermodynamics is the ideal gas assumption. We have already encountered this in Equation (4.5), the ideal gas equation of state. Our goal here is to discuss what this assumption means at the molecular scale. In fact, it means that there are no inter- molecular interactions at all—i.e., that EP,i = 0, and so all of the individual molecules are noninteracting, and behave completely independently. We thus also call them free particles.
The ideal gas is an extremely important special case, and the only one for which the statistical mechanics problem can be solved exactly. For non ideal systems, calculation of the equation of state is in principle possible, but exceedingly difficult in practice. Similar comments also apply to the calculation of key thermodynamic quantities such as the internal energy, U (Section 5.2) and the entropy, S (Section 10.4).
Note that the free particle assumption and the point particle assumption are independent—leading, e.g., to two separate vanishing terms in Equation (5.1). When both are in effect, this is described as the kinetic model, or alternatively, as an “ideal gas of point particles.” All ideal gases—whether consisting of point particles or not—give rise to the same ideal gas equation of state [Equation (4.5)].
However, the ideal gas expressions for U (Section 5.4) and for S (Section 11.4) depend on whether or not the free particles are also point particles (Section 16.2). Point particles are presumed throughout this book, unless explicitly stated otherwise [apart from the obvious exception of Equation (4.5)itself].
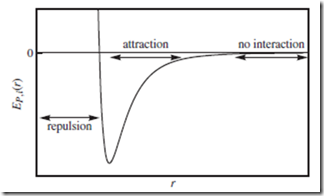
The ideal gas assumption that EP,i = 0 is rather crude; a more realistic case is portrayed in Figure 5.2—representing the intermolecular potential energy, EP,i, experienced by molecule i, as a function of its distance, r, from another molecule. For simplicity, we assume point particles—so that particle orientation plays no role, and only r matters.
At very long ranges, where r → ∞ and therefore the molar volume Vm → ∞, the particles do not interact at all; they are effectively free particles, giving rise to ideal gas behavior. At intermediate ranges, attractive forces dominate; the attraction leads to P, Z, and U values that are
Figure 5.2 Intermolecular interaction potential. Typical intermolecular interaction potential energy, EP,i , for a single point particle, i, as a function of distance, r, from another point particle. At close range, the particle feels the very steep “repulsive wall.” At intermediate ranges, there is an intermolecular attraction. At very long ranges, the particles do not interact at all, and are effectively “free.”
smaller than the ideal values. At very close range, EP,i is large and positive, and the two particles feel very strong repulsive forces pushing them apart. Macroscopically, this manifests as larger-than-ideal P, Z, and U values, as Vm → 0.
Equipartition Theorem & Temperature
According to the kinetic model, for an ideal gas of point particles, the only nonvanishing contribution to Equation (5.1) is the kinetic energy contribution,
There is an important result (end of Section 6.2) from statistical mechanics that states the following:
Equipartition Theorem: For a system in thermal equilibrium, the statistically averaged kinetic energy contribution from each velocity coordinate is the same.
In other words, every term in the sum in Equation (5.5) has the same value; every coordinate carries the same amount of kinetic energy, on aver- age. This is true regardless of the velocity component, x, y, or z, or of the particular molecule, i—or even of the type of molecule. This is a profoundly important result.
Since the above averages all have the same value, and since this value remains constant over time, we can regard it to be a true thermodynamic quantity. This is, in fact, what we use to define the temperature, as follows:
Definition 5.2 For a system in thermal equilibrium, the temperature, denoted ‘T’, is defined in relation to the average kinetic energy of each velocity coordinate, as follows:
For more general ideal gases, there are also rotational coordinates that contribute to the molecular kinetic energy, and to which the equipartition theorem also applies. Thus, the general (rotating) ideal gas expression is
Note that for ideal gases, the state function U(T, V ) depends only on the thermodynamic variable T, not on V . This is due to the lack of inter- molecular interactions—as a consequence of which, the intermolecular dis- tance r, and thus the molar volume Vm, have no effect on the energy. Thus, for ideal gases, U and T are basically the same “thermodynamic energy” quantity—with U being the extensive version, and T the intensive version.
Recall that U(T, V ) definitely does depend on V in the non-ideal case— in a manner that can be qualitatively understood, as already described in Section 5.3.