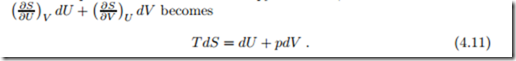Entropy as Property: The Gibbs Equation
Since T and p are intensive, and U and V are extensive properties, entropy is extensive. The specific entropy s = S/m can be computed from the Gibbs equation for specific properties, which is obtained by division of (4.11) with the constant mass m,
The Gibbs equation gives a large number of relations and restrictions between properties, in particular it allows to determine property relations for entropy.
Entropy, just as internal energy, cannot be measured directly. Property relations for entropy are computed from the Gibbs equation, and the thermal and caloric equations of state, p (T, v) and u (T, v). Here, we consider this for incompressible substances and for ideal gases.
For incompressible liquids and solids, the specific volume is constant, hence dv = 0. The caloric equation of state (3.18) implies du = cdT and the Gibbs equation reduces to T ds = cdT . For constant specific heat, c = const., integration gives entropy as explicit function of temperature,
where s0 is the entropy at the reference temperature T0. As long as no chemical reactions are involved, the definition of the entropy scale, i.e., the value of s0, can be freely chosen; the third law of thermodynamics will fix the scale properly.
For an ideal gas we have du = cv dT and v = RT /p so that the Gibbs equation (4.13) becomes
T-S-Diagram
Solving the first law for reversible processes (3.13) for heat and comparing the result with the Gibbs equation we find, with Q˙ dt = δQ,
We recall that heat is a path function, i.e., δQ is an inexact differential, but entropy is a state property, i.e., dS is an exact differential. In the language of mathematics, the inverse thermodynamic temperature 1 serves as an integrating factor for δQ, such that dS = 1 δQ becomes an exact differential.
From the above, we see that for reversible processes δQ = T dS. Accordingly, the total heat exchanged in a reversible process can be computed from temperature and entropy as the area below the process curve in the temperature-entropy diagram (T-S-diagram),
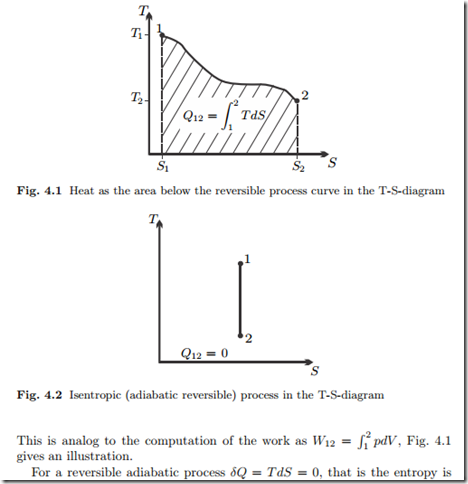
constant in the process. We say a reversible adiabatic process is isentropic.
The process curve in the T-S-diagram is a vertical line, see Fig. 4.2.