What Is Entropy?
The arguments that gave us the second law and entropy as a property centered around the trend to equilibrium observed in any system left to itself (isolated system). Based on the derivation, the question What is entropy? can be answered simply by saying It’s a quantity that arises when one constructs an inequality that describes the trend to equilibrium. Can there be a deeper understanding of entropy?
Before we try to answer, we look at internal energy: When the first law of thermodynamics was found, the concept of internal energy was new, and it was difficult to understand what it might describe. At that time, the atomic structure of matter was not known, and internal energy could not be interpreted—it appeared because it served well to describe the phenomena. Today we know more, and we understand internal energy as the kinetic and potential energies of atoms and molecules on the microscopic level. Thus, while the concept of internal energy arose from the desire to describe phenomena, today it is relatively easy to understand, because it has a macroscopic analogue in mechanics.
Entropy also came into play to describe the phenomena, but it is a new quantity, without a mechanical analogue. A deeper understanding of entropy can be gained, as for internal energy, from considerations on the atomic scale. Within the framework of his Kinetic Theory of Gases, Ludwig Boltzmann (1844-1905) found a microscopic interpretation of entropy, where entropy is related to concepts of probability. A not too precise description of this interpretation follows below.
Macroscopically, a state is described by only a few macroscopic proper- ties, e.g., temperature, pressure, volume. Microscopically, a state is described through the location and momentum of all atoms within the system. The microscopic state is constantly changing due to the microscopic motion of the atoms, and there are many microscopic states that describe the same macroscopic state. If we denote the total number of all microscopic states that describe the same macroscopic state by Ω, then the entropy of the macroscopic state according to Boltzmann is
The constant ![]() is the Boltzmann constant, which can be interpreted as the gas constant per particle.
is the Boltzmann constant, which can be interpreted as the gas constant per particle.
The growth of entropy in an isolated system, dS ≥ 0, thus means that the system shifts to macrostates which have larger numbers of microscopic realizations. Equilibrium states have particularly large numbers of realizations, and this is why they are observed.
To make the ideas somewhat clearer, we consider the expansion of a gas when a barrier is removed, see Secs. 3.13, 4.13. This is a particularly simple case, where the internal energy, and thus the distribution of energy over the particles, does not change. Hence, we can ignore the distribution of thermal energy over the particles, and the exchange of energy between them.
We assume a system of N gas particles in a volume V . The volume of a single particle is v0, and in order to be able to compute the number Ω, we “quantize” the accessible volume V into n = V/v0 boxes that each can accommodate just one particle. Note that in a gas, where the distance between individual particles is relatively large, most boxes are empty. Due to their thermal energy, the atoms move from box to box. The number of microstates is simply given by the number of realizations of a state with N filled boxes and (n − N ) empty boxes, which is
In an ideal gas the number of possible positions n is much bigger than the number of particles N , that is N Taylor expansion yields the entropy difference to leading order as
For a macroscopic amount of gas, the particle number N is extremely large (order of magnitude ∼ 1023), so that already for a small difference in volume the ratio of microscopic realization numbers is enormous. For instance for Microscopic states change constantly due to travel of, and collisions be- tween, particles. Each of the Ω microstates compatible with the given macrostate is observed with the same probability, 1/Ω. The Ω1 microstates in which the gas is confined in the volume V1 are included in the Ω2 microstates in which the gas is confined in the larger volume V2. Thus, after removal of the barrier, there is a finite, but extremely small probability of to find all gas particles in the initial volume V1. This probability is so small that the expected waiting time for observing a return into the original volume exceeds the lifetime of the universe by many orders of magnitude. If we do not want to wait that long for the return to initial state, we have to push the gas back into the initial volume, which requires work.
In generalization of the above, we can conclude that it is quite unlikely that a portion Vν of the volume is void of particles. The corresponding probability . The average volume available for one particle is V¯ = V , and when Vν = νV¯ we find, for the large particle numbers in an macroscopic amount of gas, Pν = (1 − ν ) rv e−ν . Thus, as long as Vν is bigger than the average volume for a single particle, so that ν > 1, the probability for a void is very small. Moreover, inhomogeneous distributions are rather unlikely, since the number of homogeneous distributions is far larger than the number of strongly inhomogeneous distributions. This is why we observe homogeneous distributions in equilibrium.
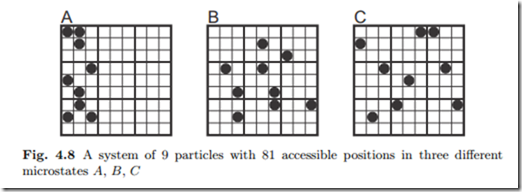
Figure 4.8 gives an illustration of microstates for a rather small system.
The system of N = 9 particles with n = 81 boxes allows for Ω = 81! = 9!(81−9)! 2.61 × 1011 microstates, three of which are shown in the figure. Microstate A is one of the Ω = 27! = 4.69 × 106 microstates in which the gas in confined to the left third of the system. Microstates B and C are more homogeneous distributions.