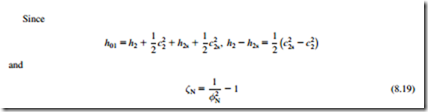The scroll and stator blades
It was pointed out by Artt and Spence (1998) that the division of losses in a radial-inflow turbine is an essential step in attaining a simple performance prediction procedure, one likely to yield useful results. A common procedure is to simply measure the static pressure at the rotor inlet tip diameter. However, without knowledge of the magnitude of the loss occurring in the stator passages the mean velocities cannot be determined.
Many different loss models for one-dimensional performance prediction methods have been published, e.g., Rohlik (1968), Benson (1970), Benson et al. (1968), Spence and Artt (1997), Whitfield (1990), etc. These range from simple loss factors determined from experimental data to more credible attempts at estimating the friction losses in a blade passage. A common fault in most of these loss models was the lack of verification from reliable experimental data. This unsatisfac- tory state of affairs still holds true. Spence and Artt (1997) published performance data of tests done on a 99 mm turbine rotor tested with seven different sized stator diameters embracing a wide range of rotor speeds and pressure ratios. Despite the ensuing comprehensive test program, these tests were not successful in providing the answers required.
It is worth trying to understand the procedure followed in these tests. The static pressure p2 was measured just outside the rotor inlet diameter. An isentropic analysis was carried out to determine the stator loss from p2. The flow was assumed to accelerate isentropically through the nozzle throat, the law of continuity enabling the velocity and ideal static pressure and static temperature to be determined. Conservation of angular momentum was then assumed to apply from the nozzle throat to the rotor inlet. The radial component of velocity at rotor inlet was found from the continuity equation applied to the cylindrical potion of the rotor inlet. Solving for these measurements by iteration enabled the ideal velocity, static temperature and pressure at the rotor inlet to be found. The measured static pressure was lower than the ideal calculated value and this difference was equated to the loss through the stator. All of this seemed straightforward enough. However, the resulting pressure loss turned out to be a strong function of the assumed angle of flow through the throat. Assuming a flow angle perpendicular to the geometric nozzle throat predicted a loss in excess of the total loss measured for the turbine stage. Using a flow angle determined from the cos21(o/s) proposed by Hiett and Johnston (1964), resulted in a loss of a more believable magnitude. For the 5.5-mm-diameter nozzle, the angle measured perpendicular to the throat was 62.7o from the radial direction, compared with 75.2o calculated from the cosine rule. The author decided to abandon this method of analysis since it is difficult to justify any angle other than one that is perpendicular to the throat.
Stator loss models
Clearly some theoretical method would be needed to estimate the stator loss. With this the rotor inlet velocity triangles and the rotor losses should then be determinable. Many loss models have been proposed for correlating the scroll and nozzle losses from performance data, but surprisingly few have been successful at predicting the losses based on the geometry alone. One of the main drawbacks with any of the simple loss models is the heavy reliance on existing test data in order to determine a loss coefficient. Also, no account is taken of the geometrical details of the blades. Rohlik (1968) used a more complex stator loss model requiring little empirical data when he presented a design procedure for radial-inflow turbines. This related boundary layer momentum thick- ness, blade geometry, energy level, and friction loss in the blade passages of axial-flow machines. A single equation (which originated from Stewart, Witney, and Wong, 1960) was given for the overall loss in a blade row:
This analysis has the advantage of requiring little empirical input data, none of which has to be derived from measured performance data of the turbine being examined. Although there were other analytical models that were examined only the model presented by Rohlik has the firmest foundation. It was the only model of many that correctly predicted the loss changes that occur for different sized nozzles.
Effects of varying the vaneless space and the vane solidity
An extensive experimental program of tests have been reported by Simpson, Spence, and Watterson (2013) carried out on a 135-mm-tip diameter radial turbine with a variety of stator vane designs. The purpose of these tests was to determine the effects that the parameter Rte=Rle2 and the vane solidity had on the stage efficiency. The authors used computational fluid dynamics and reported that it was a reliable tool in predicting trends of both stage efficiency and mass flow. Performance tests were carried out on two series of vaned stator designs in order to measure the efficiency variations with varying values of the parameters Rte=Rle and solidity c/s. It was found that the aerodynamic optimum values for these two parameters were 1.175 and 1.25, respectively. Increasing the values of both of these parameters led to a reduction of both the measured and predicted static pressure variations at the rotor inlet.
An interesting finding for designers was that increasing the size of the vaneless space was a more aerodynamically efficient method of obtaining a more circumferentially uniform flow around the rotor periphery.
Loss coefficients used in 90o IFR turbines
There are a number of ways of representing the losses in the passages of 90o IFR turbines and these have been listed and interrelated by Benson (1970). As well as the nozzle and rotor passage losses, there is a loss at rotor entry at off-design conditions. This occurs when the relative flow entering the rotor is at some angle of incidence to the radial vanes so that it can be called an incidence loss. It is sometimes referred to as shock loss. This is a rather misleading term because, normally, there is no shock wave.
Nozzle (or stator) loss coefficients
The enthalpy loss coefficient, which normally includes the inlet scroll and nozzle blade losses, has already been defined and is
Practical values of the flow coefficient φN for well-designed nozzle rows in normal operation are usually in the range 0.90 , φN , 0.97, therefore, 0.23 , ζN , 0.063.
Artt and Spence (1998) gave a very detailed review of the many tests made by researchers since the early 1960s on the losses occurring in the nozzles of radial-inflow turbines. They also made many of their own experimental tests on a 99-mm-diameter radial-inflow turbine with seven different nozzle throat areas at two rotor speeds. Plots were presented showing the division of the losses in the several parts of the turbine for the two rotor speeds and for each of the seven stator throat areas.
In a previous report, Spence and Artt (1997) commented that a good efficiency was obtained with a stator-rotor throat area ratio of 0.5. This area ratio seemed to the above authors to be inextricably linked to the optimum blade angles and the more even distribution of the expansion of the flow between the stator and the rotor.
Rotor loss coefficients
At either the design condition (Figure 8.4), or at the off-design condition dealt with later (Figure 8.5), the rotor passage friction losses can be expressed in terms of the following coefficients.
The enthalpy loss coefficient is