Optimum efficiency considerations
According to Abidat, Chen, Baines, and Firth (1992), the understanding of incidence effects on the rotors of radial- and mixed-flow turbines is very limited. Normally, IFR turbines are made with
radial vanes to reduce bending stresses. In most flow analyses that have been published of the IFR turbine, including all earlier editions of this text, it was assumed that the average relative flow at entry to the rotor was radial, that is, the incidence of the relative flow approaching the radial vanes was zero. The following discussion of the flow model will show that this is an oversimplification and the flow angle for optimum efficiency is significantly different from zero incidence. Rohlik (1975) had asserted that “there is some incidence angle that provides optimum flow conditions at the rotor-blade leading edge. This angle has a value sometimes as high as 40o with a radial blade.”
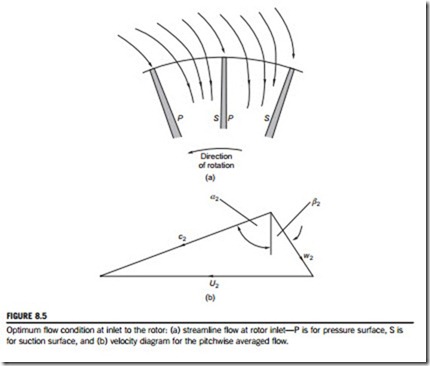
The flow approaching the rotor is assumed to be in the radial plane with a velocity c2 and flow angle α2 determined by the geometry of the nozzles or volute. Once the fluid enters the rotor, the process of work extraction proceeds rapidly with reductions in the magnitude of the tangential velocity component and blade speed as the flow radius decreases. Corresponding to these velocity changes is a high blade loading and an accompanying large pressure gradient across the passage from the pressure side to the suction side (Figure 8.5a).
With the rotor rotating at angular velocity Ω and the entering flow assumed to be irrotational, a counter-rotating vortex (or relative eddy) is created in the relative flow, whose magnitude is 2 Ω, which conserves the irrotational state. The effect is virtually the same as that described earlier for the flow leaving the impeller of a centrifugal compressor but in reverse (see Section 7.8 entitled “Slip Factor”). As a result of combining the incoming irrotational flow with the relative eddy, the relative velocity on the pressure (or trailing) surface of the vane is reduced. Similarly, on the suction (or leading) surface of the vane it is seen that the relative velocity is increased. Thus, a static pressure gradient exists across the vane passage in agreement with the reasoning of the preceding paragraph.
Figure 8.5(b) indicates the average relative velocity, w2, entering the rotor at angle β2 and giving optimum flow conditions at the vane leading edge. As the rotor vanes in IFR turbines are assumed to be radial, the angle β2 is an angle of incidence, and as drawn it is numerically positive. Depending upon the number of rotor vanes, this angle may be between 20o and 40o. The
static pressure gradient across the passage causes a streamline shift of the flow towards the suction surface. Stream function analyses of this flow condition show that the streamline pattern properly locates the inlet stagnation point on the vane leading edge so that this streamline is approximately radial (Figure 8.5a). It is reasoned that only at this flow condition will the fluid move smoothly into the rotor passage. Thus, it is the averaged relative flow that is at an angle of incidence β2 to the vane. Whitfield and Baines (1990, chap. 8) have comprehensively reviewed the computational methods used in determining turbomachinery flows, including stream function methods.
Wilson and Jansen (1965) appear to have been the first to note that the optimum angle of incidence was virtually identical to the angle of “slip” of the flow leaving the impeller of a radially bladed centrifugal compressor with the same number of vanes as the turbine rotor. Following Whitfield and Baines (1990, chap. 8), an incidence factor, λ, is defined, analogous to the slip factor used in centrifugal compressors:
To determine the relative flow angle, β2, we need to know, at least, the values of the flow coefficient, φ2 5 cm2/U2, and the vane number, Z. A simple method of determining the minimum number of vanes needed in the rotor, due to Jamieson (1955, chap. 9), is given later in this chapter. However, in the next section an optimum efficiency design method devised by Whitfield (1990) provides an alternative way for deriving β2.
3In Chapter 7, a recently modified and improved slip factor for centrifugal compressors has been presented which may have application to the analysis of radial-inflow turbines.
Design for optimum efficiency
Whitfield (1990) presented a general one-dimensional design procedure for the IFR turbine in which, initially, only the required power output is specified. The specific power output is given as
If the power output, mass flow rate, and inlet stagnation temperature are specified, then S can be directly calculated but, if only the output power is known, then an iterative procedure must be followed.
Whitfield (1990) chose to develop his procedure in terms of the power ratio S and evolved a new nondimensional design method. At a later stage of the design when the rate of mass flow and inlet stagnation temperature can be quantified, the actual gas velocities and turbine size can be determined. Only the first part of Whitfield’s method dealing with the rotor design is considered in this chapter.
Solution of Whitfield’s design problem
At the design point, it is usually assumed that the fluid discharges from the rotor in the axial direction so that with cθ3 5 0, the specific work is
which can be written as a quadratic equation for tan α2:
EXAMPLE 8.3
An IFR turbine with 12 vanes is required to develop 230 kW from a supply of dry air available at a stagnation temperature of 1050 K and a flow rate of 1 kg/s. Using the optimum efficiency design method and assuming a total-to-static efficiency of 0.81, determine
a. the absolute and relative flow angles at rotor inlet;
b. the overall pressure ratio, p01/p3;
c. the rotor tip speed and the inlet absolute Mach number.
Solution
a. From the gas tables, e.g., Rogers and Mayhew (1995) or NIST Properties of Fluids Tables, at T01 5 1050 K, we can find values for Cp 5 1.1502 kJ/kgK and γ 5 1.333. Using Eq. (8.25),