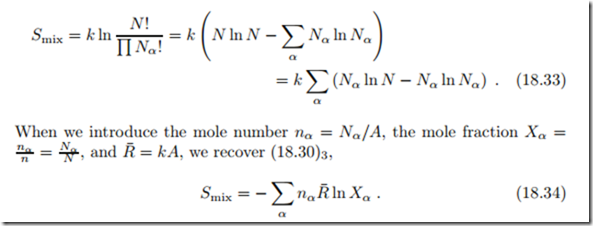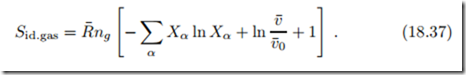Ideal Mixtures
Ideal mixtures are defined as mixtures with vanishing volume and heat of mixing, and an entropy of mixing just as that of the ideal gas, i.e.,
Ideal gas mixtures are a special case of ideal mixtures. In particular, the theory of ideal mixtures can be applied to dilute liquid solutions.
As for the ideal gas, the first two conditions (18.30)1,2 for ideal mixtures state that mixing does not affect energy. This would be the case if inter- molecular potential of the various components are equal, or at least rather similar, so that the potential energy of a pair of identical molecules (α–α-pair) is similar to that of a dissimilar pair (α–β-pair).
The entropy of mixing warrants more detailed discussion. It is best motivated through Boltzmann’s microscopic interpretation of entropy as discussed earlier, in Sec. 4.14. The microscopic definition of entropy reads
where k = R¯/A = 1.3806 × 10−23 J is Boltzmann’s constant, and Ω is the number of microscopic realizations of a given macroscopic state. For instance, for an ideal gas, simply speaking, a macroscopic state is given by the values of temperature, pressure, and velocity of the gas, while a microscopic state is given by the location and velocities of the gas particles. The entropy can be computed from (18.31) for rather complex systems, e.g., polymers, but for many systems the evaluation of the equation becomes too cumbersome to be done analytically.
A macroscopic state is for instance given by mass, volume, and temperature of a sample of substance. While the macroscopic state is maintained, due to the thermal motion of the particles the system runs through a succession of its accessible microscopic states. At standard condition, the average speed of a gas molecule is of the order of the speed of sound (∼ 350 m ), and it undergoes about 1010 collisions per second. Accordingly, the system goes through a vast number of microstates per second.
While the full evaluation of S = k ln Ω requires consideration of the full microstate, i.e., locations and velocities of particles, we can consider the lo- cations alone to compute the entropy of mixing. We study a container with N = ),α Nα particles of different types α = 1,... , ν. We divide the container into N cells of equal size, and assume that there can be only one particle per cell. Since we cannot distinguish between different particles of the same kind, the number of possibilities to distribute the ), Nα particles over the N cells is
The corresponding macrostate for a mixed state is simply to have N α Nα particles in the container.
Before we further evaluate this expression, we study the example of just four particles of two different types, two of each type. In the state before mixing, a wall separates the different components into the configuration 1 1 1 || 2 2 l. There is only one microscopic realization of this configuration, since the particles cannot pass the wall. As soon as the wall is removed, the particles can exchange positions due to thermal motion, and thus access a larger number of microstates. Equation (18.32) gives Ω = 6; the states are
Thus, the mixed state, where the wall is removed has more microscopic realizations than the unmixed state, and the higher entropy.
Note that the original configuration forms one of the accessible microstates of the unrestrained system as well. The probability that this state is 1/Ω, which is indeed the probability that any particular microstate is assumed. For real systems, the particle numbers are huge, and the number of possible configurations is enormous. The probability to find the original configuration, which was maintained by the wall before it was removed, is negligible, and most microstates will be mixed—thus mixed states will be observed.
We proceed to evaluate (18.31) with (18.32) for large numbers Nα. By means of Stirling’s formula ln N ! "’ N ln N − N , which holds for large N , we find
In thermodynamic systems the number of particles is normally very large, with 6.022×1023 particles per mole. For example in an equimolar binary mix- ture with N1 = N2 = 1023 one finds ln Ω = 1.386 × 1023, Smix = 1.9139 J .
The probability to recover the initial unmixed state as one of the microstates is incredibly small at 1 : spontaneous unmixing is not impossible, but incredibly unlikely, and cannot be expected to be observed in the lifetime of the universe. Return to Sec. 4.14 for additional discussion on the microscopic interpretation of entropy.
The computation of the entropy of mixing in this section relied on the assumption that there are as many location cells as particles, which is appropriate for simple liquids. The reader might wonder how the entropy of mixing for an ideal gas comes about, for which there are far more cells than particles. We briefly run through the necessary arguments: To deal with an ideal gas mixture, we consider empty cells as an additional species with count Ne. With N = Ng + Ne as the total number of cells and Ng = ),α Nα as number of gas particles, we have one additional term:
The first term is the entropy of mixing as discussed before. We proceed with the discussion of the second term. The total volume filled by the gas is V = N vc, where vc is the cell volume. Therefore ln N = ln v¯ , where v¯ is mole volume and v¯0 = vcA is a reference mole volume. For the ideal gas, there are far more cells than gas particles, so that N » Ng , and in the limit we contributions to ideal gas entropy, namely entropy of mixing, the well-known volume dependence of entropy, and a constant,