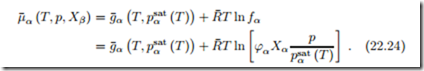Non-ideal Mixtures: Activity and Fugacity
So far, we considered only ideal mixtures. In this section, we study how non- ideal effects are incorporated into the description.
The activity coefficient γα (T, p, Xβ ) and the activity aα (T, p, Xβ ) = γα (T, p, Xβ ) Xα are defined such that the chemical potential reads
As always, g¯α (T, p) denotes the Gibbs free energy of component α alone, under the same pressure and temperature as the mixture. For ideal mixtures or ideal gases, the activity coefficient reduces to γα = 1, and the activity becomes aα = Xα.
For the description of vapors, one uses typically the fugacity coefficient the fugacity , which are defined such that
Here, g¯α (T, psat (T )) denotes the Gibbs free energy of component α alone at saturation under the same temperature as the mixture. When the vapor can be described as an ideal gas, the fugacity coefficient reduces to ϕα = 1.
Just as the chemical potential, activity and fugacity depend on the detailed composition, Xβ , of the respective phase. Thus, on the first glance, it might seem that the introduction of activity and fugacity and their coefficients has no advantage, since one replaces one unknown function, the chemical potential, with another, activity or fugacity. The latter, however, are accessible to measurements, and this is why they are used in chemical engineering.
To understand how fugacity can be measured, we consider the Gibbs equation (20.1) and take mixed derivatives with respect to p and nα, to find
The function under the integral can be measured by systematically adding component α, and determining the resulting volume change; this must be repeated for many pressures. Thus, the fugacity can be measured in the vapor phase.
Measurements of activity and activity coefficients rely on Raoult’s law. We reconsider Raoult’s law for the equilibrium between a liquid and a vapor mixture, where we now use activity and fugacity coefficients to describe the liquid and the vapor, respectively. Gibbs’ phase rule becomes
When we consider the liquid as almost incompressible, and assume that its molar volume can be ignored compared to the molar volume of the vapor,2 this reduces to
It follows that activity can be measured when fugacity is known.