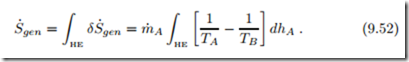Open Systems:Closed Heat Exchangers and Open Heat Exchangers,Adiabatic Mixing.

Closed Heat Exchangers

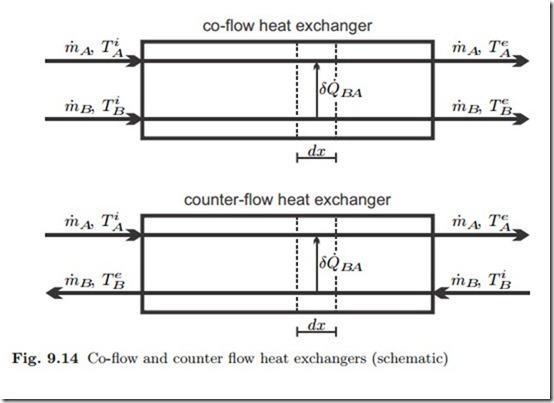
Closed heat exchangers serve to transfer heat between diﬀerent ﬂuids, for instance from the hot combustion gas to evaporating water in steam power plants, or from the condenser in the power plant to the cooling water. We ignore friction losses in the ﬂow, so that the ﬂows are isobaric. Figure 9.14 shows the exchange of heat between two ﬂuids A and B in co- and counter- ﬂow heat exchangers, where superscripts i and e denote incoming and exiting ﬂows, respectively. Since the ﬂuids ﬂow through diﬀerent piping systems, they might have diﬀerent pressures pA, pB .

The conservation laws for mass and energy give for both set-ups (adiabatic to the outside, steady state)

For a closer look, we consider the ﬁrst and second law for an inﬁnitesimal section dx of the heat exchanger (no work, kinetic and potential energies can be ignored), which read

For isobaric processes the Gibbs equation gives dh = T ds, which allows to combine the above to

Accordingly, entropy generation and lost work depend on the local temper- ature diﬀerence between the streams. The total entropy generation is given by the integral over the length of the heat exchanger (HE),

To see that the entropy generation is positive, we note that, under the given simpliﬁcations, the ﬁrst law for stream A reads m˙ AdhA = δQ˙ BA where δQ˙ BA is the heat going from B to A (heat into the system is positive). Since heat goes from warm to cold, we have δQ˙ BA > 0 if TB > TA .

A detailed discussion of counter-ﬂow and co-ﬂow heat exchangers shows that the local temperature diﬀerence between the two ﬂows is smaller for the counter-ﬂow design, which therefore is thermodynamically preferable (see Sec. 15.2).

Open Heat Exchangers: Adiabatic Mixing

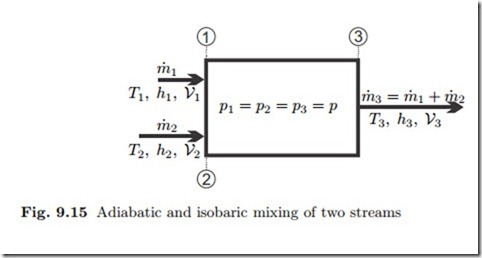
Another interesting process that occurs quite often is heat exchange be- tween two ﬂows by adiabatic mixing of two (or more) streams, as depicted in Fig. 9.15. To prevent backﬂow, the mixed streams should have the same pressure, but their temperatures and/or phase states are diﬀerent. For the computation, pressure losses through the mixing chamber are normally ignored, so that the outﬂow pressure equals the inﬂow pressure. Moreover, kinetic and potential energies can be ignored since their changes are much smaller than changes in enthalpy.

That is, the mass ﬂow and the total enthalpy ﬂow are conserved in mixing. Since mixing occurs uncontrolled, the process is irreversible, and the entropy will increase; from (9.13) we ﬁnd