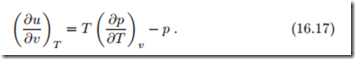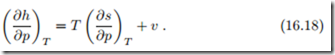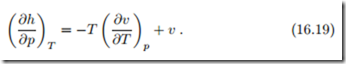Two Useful Relations
Gibbs equation and Maxwell relations can be used to obtain additional relations between properties which will form the center of the following section on measurement of thermodynamic properties. To proceed, we consider energy and entropy in the Gibbs equation (16.2) as functions of temperature and volume, u (T, v), s (T, v), and evaluate their differentials as
A faster approach to the first relation is to take the partial derivative of the Gibbs equation (16.2) with respect to v while keeping T constant. Similarly the second relation follows from taking the partial derivative of the Gibbs equation (16.2) with respect to T while keeping v constant.
With the Maxwell relation (16.11)3 to replace the entropy derivative ( ∂s ) ∂v T in (16.16)1, we find an equation for the volume dependence of internal energy that is entirely determined by the thermal equation of state p (T, v),
Since internal energy cannot be measured directly, the left hand side cannot be determined experimentally. However, the right hand side is determined by the thermal equation of state, p (T, v), which is easy to measure. The equation states that the volume dependence of the internal energy is known from measurement of the thermal equation of state.
For instance for the ideal gas p (T, v) = RT /v and thus ( ∂u ) = 0— ∂v T the internal energy of the idea gas is independent of volume, and therefore depends only on temperature, u = u (T ). While we have used this from the beginning as an experimental fact, we see here that it is a direct consequence of the Gibbs equation and the thermal equation of state.
To obtain a similar relation for enthalpy, we take the partial derivative of the Gibbs equation (16.9)1 with respect to p while keeping T constant, to obtain
With the Maxwell relation (16.13)3 to replace the entropy derivative ( ∂s , ∂p T this gives an equation for the pressure dependence of enthalpy, which is entirely determined by the thermal equation of state p (T, v), or rather v (T, p),
For instance for the ideal gas v (T, p) = RT /p and thus ( ∂h T = 0—the enthalpy of the ideal gas is independent of pressure, and depends only on temperature, h = h (T ).