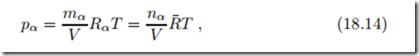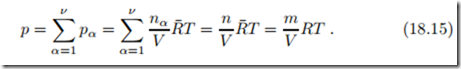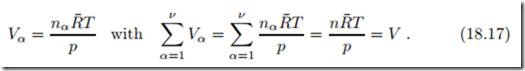Ideal Gas Mixtures
We first consider ideal gas mixtures, which are particularly simple. In ideal gases, due to the large average distance between particles, the potential energies between particles can be ignored against their microscopic kinetic energies. Then, the individual components are not affected by the presence of other components, there is no enthalpy of mixing, and the ideal gas law holds for the individual components and the mixture.2
The partial pressure of one component distributed over the mixture volume V is given by the ideal gas law
where R¯ = 8.314 kJ is the universal gas constant, and Rα = R¯/Mα. The second form of the ideal gas law shows that the behavior of all ideal gases depends only on mole number, temperature and volume, but not on the type of gas.
The total pressure is just the sum of the partial pressures. For ideal gases, where the partial pressures are unaffected by the presence of other molecules, this is known as Dalton’s law (John Dalton, 1766-1844),
Here R = R¯/M is the gas constant for the mixture and M is the mixture’s mean molar mass (18.5). Thus, with the proper molar masses, the components and the mixture obey the ideal gas law.
Division of the ideal gas laws for the component and the mixture shows that for ideal gas mixtures the pressure ratio equals the mole ratio,
In case that the ideal gas mixture is separated, so that each individual component is at the mixture pressure p and temperature T in its own volume Vα, the ideal gas law for the components reads
Here, V is the volume of the mixture in the mixed state. This is Amagat’s law (E´ mile Amagat 1841-1915) which states that there will be no volume change when ideal gases are mixed, Vmix = 0, as long as the pressures and temperatures before and after mixing are the same.