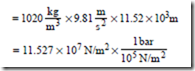Vacuum gauges
Vacuum gauges are instruments for giving a visual indication, by means of a pointer, of the amount by which the pressure of a fluid applied to the gauge is less than the pressure of the surrounding atmosphere. Two examples of vacuum gauges are the McLeod gauge and the Pirani gauge.
McLeod gauge
The McLeod gauge is normally regarded as a standard and is used to calibrate other forms of vacuum gauges. The basic principle of this gauge is that it takes a known volume of gas at a pressure so low that it cannot be measured, then compresses the gas in a known ratio until the pressure becomes large enough to be measured by an ordinary manometer. This device is used to measure low pressures, often in the range 10–6 to 1.0 mm of mercury. A disadvantage of the McLeod gauge is that it does not give a continuous reading of pressure and is not suitable for registering rapid variations in pressure.
Pirani gauge
The Pirani gauge measures the resistance and thus the temperature of a wire through which current is flowing. The thermal conductivity decreases with the pressure in the range 10–1 to 10–4 mm of mercury so that the increase in resistance can be used to measure pressure in this region. The Pirani gauge is calibrated by comparison with a McLeod gauge.
Hydrostatic pressure on submerged surfaces
From Section 22.2, it can be seen that hydrostatic pressure increases with depth according to the formula:
p = ρgh
Problem 10. The deepest part of the oceans is the Marianas Trench, where its depth is approximately 11.52 km (7.16 miles). What is the gauge pressure at this depth, assuming that ρ = 1020 kg/m3 and g = 9.81 m/s2?
Gauge pressure, p = ρgh
i.e. pressure, p = 1152.7 bar
Note that from the above calculation, it can be seen that a gauge pressure of 1 bar is approximately equivalent to a depth of 10 m.
Problem 11. Determine an expression for the thrust acting on a submerged plane surface, which is inclined to the horizontal by an angle θ, as shown in Figure 22.11.
Problem 12. Determine an expression for the position of the centre of pressure of the plane surface P(x′, y′) of Figure 22.11; this is also the position of the centre of thrust.
Taking moments about O gives:
Practise Exercise 120 Further problems on hydrostatic pressure on submerged surfaces
1. Determine the gauge pressure acting on the surface of a submarine that dives to a depth of 500 m. Take water density as 1020 kg/m3.
[50.03 bar]
2. Solve Problem 1, when the submarine dives to a depth of 780 m. [78.05 bar]
3. If the gauge pressure measured on the surface of the submarine of Problem 1 were 92 bar, at what depth has the submarine dived to? [919.4 m]
4. A tank has a flat rectangular end, which is of size 4 m depth by 3 m width. If the tank is filled with water to its brim and the flat end is vertical, determine the thrust on this end and the position of its centre of pressure. Take water density as 1000 kg/m3.
[0.235 MN; 2.667 m]
5. If another vertical flat rectangular end of the tank of Problem 4 is of size 6 m depth by 4 m width, determine the thrust on this end and position of the centre of pressure. The depth of water at this end may be assumed to be 6 m. [0.706 MN; 4 m]
6. A tank has a flat rectangular end, which is inclined to the horizontal surface, so that θ = 30°, where θ is as defined in Figure 22.11, page 254. If this end is of size 6 m height and 4 m width, determine the thrust on this end and the position of the centre of pressure from the top. The tank may be assumed to be just full.
[0.235 MN; 2 m]