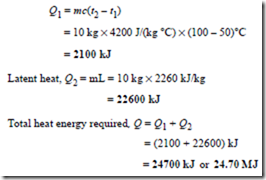Heat energy and transfer: Latent heats of fusion and vaporisation

Latent heats of fusion and vaporisation

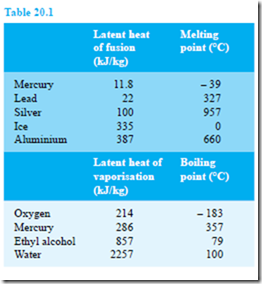
The specific latent heat of fusion is the heat required to change 1 kg of a substance from the solid state to the liquid state (or vice versa) at constant temperature. The specific latent heat of vaporisation is the heat required to change 1 kg of a substance from a liquid to a gaseous state (or vice versa) at constant temperature. The units of the specific latent heats of fusion and vaporisation are J/kg, or more often kJ/kg, and some typical values are shown in Table 20.1

The quantity of heat Q supplied or given out during a change of state is given by:

Q = mL

where m is the mass in kilograms and L is the specific latent heat.

Thus, for example, the heat required to convert 10 kg of ice at 0°C to water at 0°C is given by

10 kg × 335 kJ/kg = 3350 kJ or 3.35 MJ

Besides changing temperature, the effects of supplying heat to a material can involve changes in dimensions, as well as in colour, state and electrical resistance. Most substances expand when heated and contract when cooled, and there are many practical applications and design implications of thermal movement (see Chapter 21).

Problem 10. How much heat is needed to melt completely 12 kg of ice at 0°C ? Assume the latent heat of fusion of ice is 335 kJ/kg.

Quantity of heat required,

Q = mL = 12 kg × 335 kJ/kg

= 4020 kJ or 4.02 MJ

Problem 11. Calculate the heat required to convert 5 kg of water at 100°C to superheated steam at 100°C. Assume the latent heat of vaporisation of water is 2260 kJ/kg.

Quantity of heat required,

Q = mL = 5 kg × 2260 kJ/kg

= 11300 kJ or 11.3 MJ

Problem 12. Determine the heat energy needed to convert 5 kg of ice initially at – 20°C completely to water at 0°C. Assume the specific heat capacity of ice is 2100 J/(kg °C) and the specific latent heat of fusion of ice is 335 kJ/kg.

Problem 13. Calculate the heat energy required to convert completely 10 kg of water at 50°C into steam at 100°C, given that the specific heat capacity of water is 4200 J/(kg °C) and the specific latent heat of vaporisation of water is 2260 kJ/kg.

Quantity of heat required = sensible heat + latent heat.
Sensible heat

Problem 14. Determine the amount of heat energy needed to change 400 g of ice, initially at –20°C, into steam at 120°C. Assume the following: latent heat of fusion of ice = 335 kJ/kg, latent heat of vaporisation of water = 2260 kJ/kg, specific heat capacity of ice = 2.14 kJ/(kg °C), specific heat capacity of water = 4.2 kJ(kg °C) and specific heat capacity of steam = 2.01 kJ/(kg °C).

The energy needed is determined in five stages:

(i) Heat energy needed to change the temperature of ice from – 20°C to 0°C is given by:

Q1 = mc(t2 – t1)

= 0.4 kg × 2.14 kJ/(kg °C) × (0 – – 20)°C

= 17.12 kJ

(ii) Latent heat needed to change ice at 0°C into water at 0°C is given by:

Q2 = mLf = 0.4 kg × 335 kJ/kg = 134 kJ

(iii) Heat energy needed to change the temperature of water from 0°C (i.e. melting point) to 100°C

(i.e. boiling point) is given by:

(iv) Latent heat needed to change water at 100°C into steam at 100°C is given by:

Q4 = mLv = 0.4 kg × 2260 kJ/kg = 904 kJ

(v) Heat energy needed to change steam at 100°C into steam at 120°C is given by:

Now try the following Practise Exercise

Practise Exercise 109 Further problems on the latent heats of fusion and vaporisation

1. How much heat is needed to melt completely 25 kg of ice at 0°C. Assume the specific latent heat of fusion of ice is 335 kJ/kg.

[8.375 MJ]

2. Determine the heat energy required to change 8 kg of water at 100°C to superheated steam at 100°C. Assume the specific latent heat of vaporisation of water is 2260 kJ/kg.

[18.08 MJ]

3. Calculate the heat energy required to convert 10 kg of ice initially at – 30°C completely into water at 0°C. Assume the specific heat capacity of ice is 2.1 kJ/(kg °C) and the specific latent heat of fusion of ice is 335 kJ/kg.

[3.98 MJ]

4. Determine the heat energy needed to convert completely 5 kg of water at 60°C to steam at 100°C, given that the specific heat capacity of water is 4.2 kJ/(kg °C) and the specific latent heat of vaporisation of water is 2260 kJ/kg. [12.14 MJ]

A simple refrigerator

The boiling point of most liquids may be lowered if the pressure is lowered. In a simple refrigerator a working fluid, such as ammonia or freon, has the pressure acting on it reduced. The resulting lowering of the boiling point causes the liquid to vaporise. In vaporising, the liquid takes in the necessary latent heat from its surroundings, i.e. the freezer, which thus becomes cooled. The vapour is immediately re- moved by a pump to a condenser that is outside of the cabinet, where it is compressed and changed back into a liquid, giving out latent heat. The cycle is repeated when the liquid is pumped back to the freezer to be vaporised.

Conduction, convection and radiation

Heat may be transferred from a hot body to a cooler body by one or more of three methods, these being: (a) by conduction (b) by convection or (c) by radiation.

Conduction

Conduction is the transfer of heat energy from one part of a body to another (or from one body to another) without the particles of the body moving.

Conduction is associated with solids. For example, if one end of a metal bar is heated, the other end will become hot by conduction. Metals and metallic alloys are good conductors of heat, whereas air, wood, plastic, cork, glass and gases are examples of poor conductors they are heat insulators).

Practical applications of conduction include:

(i) A domestic saucepan or dish conducts heat from the source to the contents. Also, since wood and plastic are poor conductors of heat they are used for saucepan handles.

(ii) The metal of a radiator of a central heating sys- tem conducts heat from the hot water inside to the air outside.

Convection

Convection is the transfer of heat energy through a substance by the actual movement of the substance it- self. Convection occurs in liquids and gases, but not in solids. When heated, a liquid or gas becomes less dense. It then rises and is replaced by a colder liquid or gas and the process repeats. For example, electric kettles and central heating radiators always heat up at the top first.

Examples of convection are:

(i) Natural circulation hot water heating systems depend on the hot water rising by convection to the top of the house and then falling back to the bottom of the house as it cools, releasing the heat energy to warm the house as it does so.

(ii) Convection currents cause air to move and there- fore affect climate.

(iii) When a radiator heats the air around it, the hot air rises by convection and cold air moves in to take its place.

(iv) A cooling system in a car radiator relies on convection.

(v) Large electrical transformers dissipate waste heat to an oil tank. The heated oil rises by convection to the top, then sinks through cooling fins, losing heat as it does so.

(vi) In a refrigerator, the cooling unit is situated near the top. The air surrounding the cold pipes be- come heavier as it contracts and sinks towards the bottom. Warmer, less dense air is pushed upwards and in turn is cooled. A cold convection current is thus created.

Radiation

Radiation is the transfer of heat energy from a hot body to a cooler one by electromagnetic waves. Heat radiation is similar in character to light waves – it travels at the same speed and can pass through a vacuum – except that the frequency of the waves is different. Waves are emitted by a hot body, are trans- mitted through space (even a vacuum) and are not detected until they fall on to another body. Radiation is reflected from shining, polished surfaces but absorbed by dull, black surfaces.