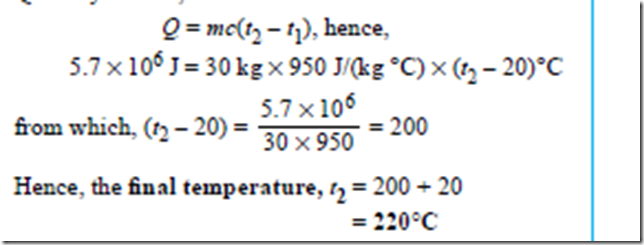Specific heat capacity
The specific heat capacity of a substance is the quantity of heat energy required to raise the temperature of 1 kg of the substance by 1°C. The symbol used for specific heat capacity is c and the units are J/(kg °C) or J/(kg K). (Note that these units may also be written as J kg–1 °C–1 or J kg–1 K–1).
Some typical values of specific heat capacity for the range of temperature 0°C to 100°C include:
Hence to raise the temperature of 1 kg of iron by 1°C requires 500 J of energy, to raise the temperature of 5 kg of iron by 1°C requires (500 × 5) J of energy, and to raise the temperature of 5 kg of iron by 40°C re- quires (500 × 5 × 40) J of energy, i.e. 100 kJ.
In general, the quantity of heat energy, Q, required to raise a mass m kg of a substance with a specific heat capacity of c J/(kg °C), from temperature t1 °C to t2 °C is given by:
Q = mc(t2 – t1) joules
Problem 3. Calculate the quantity of heat required to raise the temperature of 5 kg of water from 0°C to 100°C. Assume the specific heat capacity of water is 4200 J/(kg °C).
Quantity of heat energy,
Q = mc(t2 – t1)
= 5 kg × 4200 J/(kg °C) × (100 – 0)°C
= 5 × 4200 × 100
= 2100000 J or 2100 kJ or 2.1 MJ
Problem 4. A block of cast iron having a mass of 10 kg cools from a temperature of 150°C to 50°C.
How much energy is lost by the cast iron? Assume the specific heat capacity of iron is 500 J/(kg °C).
Quantity of heat energy,
Q = mc(t2 – t1)
= 10 kg × 500 J/(kg °C) × (50 – 150)°C
= 10 × 500 × (–100)
= – 500000 J or – 500 kJ or – 0.5 MJ
(Note that the minus sign indicates that heat is given out or lost).
Problem 5. Some lead having a specific heat capacity of 130 J/(kg °C) is heated from 27°C to its melting point at 327°C. If the quantity of heat required is 780 kJ, determine the mass of the lead.
Quantity of heat, Q = mc(t2 – t1), hence,
780 × 103 J = m × 130 J/(kg °C) × (327 – 27)°C i.e. 780000 = m × 130 × 300
from which, mass, m = 780000/130*300 kg = 20 kg
Problem 6. 273 kJ of heat energy are required to raise the temperature of 10 kg of copper from 15°C to 85°C. Determine the specific heat capacity of copper.
Quantity of heat, Q = mc(t2 – t1), hence:
273 × 103 J = 10 kg × c × (85 – 15)°C
where c is the specific heat capacity,
i.e. 273000 = 10 × c × 70
from which, specific heat capacity, c =
273000/10 × 70
= 390 J/(kg °C
Problem 7. 5.7 MJ of heat energy are supplied to 30 kg of aluminium that is initially at a temperature of 20°C. If the specific heat capacity of aluminium is 950 J(kg°C), determine its final temperature.
of 20°C. If the specific heat capacity of aluminium is 950 J(kg°C), determine its final temperature.
Quantity of heat,
Problem 8. A copper container of mass 500 g contains 1 litre of water at 293 K. Calculate the quantity of heat required to raise the temperature of the water and container to boiling point, assuming there are no heat losses. Assume that the specific heat capacity of copper is 390 J/(kg K), the specific heat capacity of water is 4.2 kJ(kg K) and 1 litre of water has a mass of 1 kg.
Heat is required to raise the temperature of the water, and also to raise the temperature of the copper container.
Practise Exercise 107 Further problems on specific heat capacity
1. Determine the quantity of heat energy (in megajoules) required to raise the tem- perature of 10 kg of water from 0°C to 50°C. Assume the specific heat capacity of water is 4200 J/(kg °C). [2.1 MJ]
2. Some copper, having a mass of 20 kg, cools from a temperature of 120°C to 70°C. If the specific heat capacity of copper is 390 J/(kg °C), how much heat energy is lost by the copper ? [390 kJ]
3. A block of aluminium having a specific heat capacity of 950 J/(kg °C) is heated from 60°C to its melting point at 660°C. If the quantity of heat required is 2.85 MJ, de- termine the mass of the aluminium block. [5 kg]
4. 20.8 kJ of heat energy is required to raise the temperature of 2 kg of lead from 16°C to 96°C. Determine the specific heat capacity of lead. [130 J/kg °C]
5. 250 kJ of heat energy is supplied to 10 kg of iron which is initially at a temperature of 15°C. If the specific heat capacity of iron is 500 J/(kg °C) determine its final tempera- ture. [65°C]
Change of state
A material may exist in any one of three states – solid, liquid or gas. If heat is supplied at a constant rate to some ice initially at, say, –30°C, its temperature rises as shown in Figure 20.1. Initially the temperature in- creases from –30°C to 0°C as shown by the line AB. It then remains constant at 0°C for the time BC required for the ice to melt into water.
When melting commences the energy gained by continual heating is offset by the energy required for the change of state and the temperature remains constant even though heating is continued. When the ice is completely melted to water, continual heating raises the temperature to 100°C, as shown by CD in Figure 20.1. The water then begins to boil and the temperature
again remains constant at 100°C, shown as DE, until all the water has vaporised.
Continual heating raises the temperature of the steam as shown by EF in the region where the steam is termed superheated.
Changes of state from solid to liquid or liquid to gas occur without change of temperature and such changes are reversible processes. When heat energy flows to or from a substance and causes a change of temperature, such as between A and B, between C and D and be- tween E and F in Figure 20.1, it is called sensible heat (since it can be ‘sensed’ by a thermometer).
Heat energy which flows to or from a substance while the temperature remains constant, such as be- tween B and C and between D and E in Figure 20.1, is called latent heat (latent means concealed or hidden).
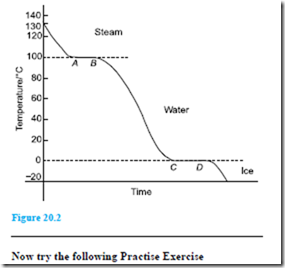
Problem 9. Steam initially at a temperature of 130°C is cooled to a temperature of 20°C below the freezing point of water, the loss of heat energy being at a constant rate. Make a sketch, and briefly explain, the expected temperature/time graph rep- resenting this change.
A temperature/time graph representing the change is shown in Figure 20.2. Initially steam cools until it reaches the boiling point of water at 100°C. Tempera- ture then remains constant, i.e. between A and B, even though it is still giving off heat (i.e. latent heat). When all the steam at 100°C has changed to water at 100°C it starts to cool again until it reaches the freezing point of water at 0°C. From C to D the temperature again remains constant (i.e. latent heat), until all the water is converted to ice. The temperature of the ice then decreases as shown.
Practise Exercise 108 A further problem on change of state
1. Some ice, initially at – 40°C, has heat sup- plied to it at a constant rate until it becomes superheated steam at 150°C. Sketch a typical temperature/time graph expected and use it to explain the difference between sensible and latent heat.
[Similar to Figure 20.1, page 228]
Related posts:
Incoming search terms:
- Enfuse 50c/s Boregan Sp 1Kg 3c/s
- calculate the temperature change when 1000J of heat is supplied to 100g of water
- 7 5kg of water at 50oc is mixed with 5kg of water at 95oc what is the final steady temperature of the mixture
- When heat of temperature of 130 decree is applied to copper of mass 500g
- 91 Draw Furnaces mail
- how many calories of energy are transfered when 10ml of water cool to a temperature of 20 degrees from a temperature of80 degrees? assume the des=nsity of water is 1g/ml and the specific heat capacity of water is 1 cal per gram degree celcius
- specific heat capacity of water
- Solve A machine with an input power of 2kw up 80% of d power If all the remaining energy appears as heat and heat up 40kg of iron what will be the rise in temperature this iron in 2min
- Calculate the tempreture change when 1000j of heat is supplied to 100g of water
- amount of heat required for 200g water to heat from 20C to 40C
- What is the specific heat capacity if it takes 1000J of energy to heat 25g of this substance by 100°C?
- calculate the temperature change when 1000 j of heat is supplied to 100g of water solve it now
- what is the energy reqired to increase 1 degree on! kg of iron block==================== iron block
- amount of heat required for 200g water to heat from 20°c to 40°c
- A cooking pan is made of aluminium of mass 2kg and a specific heat value of 0 95 kJ/kg K The pan is filled with 5 litres of water of density 1000 kg/m3 and specific heat capacity of 4 2 kJ/kg K If the pan and water are at a room temperature of 200 C how m
- An aluminium calorimeter of mass 0 05kg is filled with 230cm^3 water and 75g of melting ice in thermal equilibrium An unknown metal cube of mass 300g and temperature of 250∘C is added to the calorimeter The final temperature of the system is 30∘C
- Ablock of copper of mass 2kg and specific heat capacity 400j/kgk initially at 81 oC is immersed in water at 20 oC If the final temperature is 21 oC determine the mass of water
- How much heat energy is needed to change 10 kg of water at 50 C to steam at 120 C?
- how much heat is needed to boil iron
- 600 g of iron is at a particular temperature What will be its change in the temperature if you are using 8 000 calories? Specific heat of the Iron (0 113 cal/g°C) (475 J/kg°C)
- 1kg of water to 0 degree celcius from 25 energy needed
- An electric heater raises the temperature of 10K in 2min when placed in 70g of water contained
- c If the specific heat capacity of copper is 0 394 KJ/ (Kg 0C) how much heat is lost by a block of copper of mass 100 Kg when it cools down from 100 to 50 0C
- calculate the amount of heat required to raise the temperature of 102 kg of copper from 10 degree celsius to 75-5 degree celsius
- A 0 5 kg block of aluminum (caluminum=900J/kg⋅∘C) is heated to 200∘C The block is then quickly placed in an insulated tub of cold water at 0∘C (cwater=4186J/kg⋅∘C) and sealed At equilibrium the temperature of the water and block are measured to be 20∘C qu
- A boiler used to boil water containing 100 L of water at a temperature of 25°C is placed on an electric heater (Q = 3000 J/s) Find the time at which water begins to boil
- calculate the energy required to heat853 0mgof water from32 3°cto41 9°c assume the specific heat capacity of water under these conditions is4 18·j·g−1k−1 be sure your answer has the correct number of significant digits
- Calculate the quantity of heat required to raise the temperature of 20 0 g of water from 20 7 °C to 38 6 °C
- how many joules are required to heat 100g of water from 15c to 95c?
- a heating coil of resistance 20 ohms connected to a 220v source is used to boil
- A glass bottle is filled with 0 75 kg of water at a temperature of 200C The bottle is then placed in a freezer which freezes the water and cools it to −150C (a)Calculate the energy removed from the water to reduce its temperature to 00C (b)Calculate the e
- How much heat is required to increase the temperature of 50 g of water by 1°C?
- 1 kg mass steel glass and aluminium rolls brought 1 degree celsius how many several joules and how has the internal energy of each roller changed?
- calculate the energy required to heat522 0gof water from35 1°cto44 6°c assume the specific heat capacity of water under these conditions is4 18·j·g−1k−1 be sure your answer has the correct number of significant digits
- 1 95 kJ of heat is required to raise the temperature of 500 g of lead from 59 °F to its final temperature This final temperature is (The specific heat of lead is 130 J/kg °C)
- a metallic ball requires 4 kj heat energy to raise temprature by 20 c find its heat capacity
- Calculate the heat capacity of an object with mass 1 80kg 1 80kg and specific heat capacity 0 32J g −1 K −1 0 32Jg−1K−1
- how many grams of co are required to transfer 60 kj ofheat to the surroundings?
- calculate the temperature change when 1000 j of heat is supplied to 100g of water
- Determine the heat energy required to change X kg of water at T1 ºC to superheated steam at T2 ºC given that the specific heat capacity of water is 4200 J/kg ºC the specific heat capacity of steam is 2010 J/kg ºC and the latent heat of vaporisation
- find time for 1 5 kg with 500 watt heater from 20 to 80 degrees celsius
- how many kilojoules of energy are necessary to melt 1kg iron ingot
- how much heat must be added to 5kg water to raise temperatur from 20°c to 80°c
- a copper of container of mass 500g contains 1litre of water at 293k calculate the quantity of heat required to raise the temperature of water and container to boiling point assuming there are no heat losses assume specific heat capacity of water is 4 2kj/
- attempt 2how much heat energy is required to convert60 3 g60 3 gof solid ethanol at−114 5°c−114 5°cto gasesous ethanol at155 5°c155 5°c? the molar heat of fusion of ethanol is4 60 kj/mol4 60 kj/mol and its molar heat of vaporization is38 56 kj/mol38 56 kj
- calculate the mass of water when 5kg of energy is used to heat it by 0 5 degrees celsius
- calculate the amount of heat required to raise the temperature of helium (he) from zero c to 1000 c at constant volume
- 100 g ice at – 200C is added to 100 g of water at 500C The mixture contents are : (specific heat of water = 4 2 J/g/0C specific heat of ice =2 1 J /g/0C Heat of fusion of water at 00C=334 J/g) A) 50 g ice and 150 g water at 00 C B) 50 g ice and 150 g wate
- 5kg steel is immersed in water at 20 degrees what is mass of water required if final temp is 40 degrees
- find (a) the energy absorbed as heat and (b) the change in entropy of a 2 00 kg block of copper whose temperature is increased reversibly from 25 0°c to 100°c the specific heat of copper is 386 j/kg%k