Compression with Intercooling
The work required in a reversible compressor which compresses an ideal gas from pressure p1 to pressure p2 is given by Eq. (9.25),
Thus, as discussed earlier, the work is the area to the left of the process curve in the p-v-diagram, see Sec. 9.6; less work is required for smaller specific volume of the compressed substance.
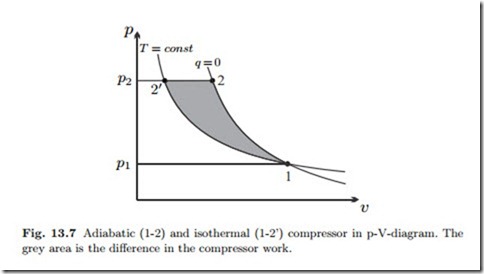
Figure 13.7 shows the curves for an isothermal and an adiabatic compressor in the p-v-diagram, in the reversible case. The adiabatic curve is steeper than the isothermal curve (Sec. 7.7), since in the isothermal process the cooling during compression ensures a smaller specific volume. Therefore the isothermal compressor requires less work than the adiabatic one.
For an isothermal compressor we have v = RT1/p, and the work is wC = −RT1 ln p2 , while for an adiabatic compressor, assuming constant specific heats, we have v = v1 (p1/p)1/k and wc = cpT1 . The difference in work requirement is indicated by the shaded area in the figure.
Obviously, to reduce the work requirement one would aim at isothermal compression. However, isothermal compression requires cooling during compression which is impossible to achieve for the large throughputs required, and cannot be used in practice.
An alternative is offered by multi-stage compressors with intercooling, in which the gas is compressed adiabatically in each stage, and then isobarically cooled to the environmental temperature T1 before it enters the next stage. Intercooling reduces the gas volume, and thus the work requirement is reduced. As an example, Fig. 13.8 shows a three stage compressor with inter- cooling. As more stages are used, the process curve approaches the isothermal curve. It should be noted that construction is more costly than for a single stage compressor.
The work savings depend on the pressures chosen for intercooling, which must be optimized. We consider an n-stage compressor which takes in gas at p1, T1, and compresses it to the final pressure pe; between each stage the gas is cooled back to T1. Stage i compresses from T1, pi to pi+1, and requires the work
The reversible work is a monotonous function of the pressure ratio. It follows that the multi-stage compressor requires minimum work when all stages operate at the same pressure ratio P , i.e.,
This implies that all stages consume the same work per unit mass, wC (P ). Multiplication of the pressure ratios of all stages gives, with pn+1 = pe,
In case that the isentropic compressor efficiency depends on the pressure within the compressor, one has to evaluate (13.14). We note that the aboveargument is valid also for polytropic compressors, as long as the polytropic exponent for all compressors is the same.