Bernoulli’s equation
Bernoulli’s equation states that for a fluid flowing through a pipe from section 1 to section 2:
v1 = velocity at section 1,
v2 = velocity at section 2,
z1 = ‘height’ of pipe at section 1,
z2 = ‘height’ of pipe at section 2,
hf = friction losses (in m) due to the fluid flowing
from section 1 to section 2,
and g = 9.81 m/s2 (assumed).
Problem 2. A storage tank contains oil whose free surface is 5 m above an outlet pipe, as shown in Figure 23.12. Determine the mass rate of flow at the exit of the outlet pipe, assuming that (a) losses at the pipe entry = 0.4 v2, and (b) losses at the valve = 0.25 v2. Pipe diameter = 0.04 m, density of oil, ρ = 770 kg/m3
Flow through an orifice
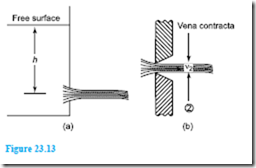
Consider the flow of a liquid through a small orifice, as shown in Figures 23.13(a) and (b), where it can be seen that the vena contracta (VC) lies just to the right of the orifice. The cross-sectional area of the fluid is the smallest here and its decrease in area from the orifice is measured by the coefficient of contraction (Cc).
Due to friction losses there will be a loss in velocity at the orifice; this is measured by the coefficient of velocity, namely Cv, so that:
Now try the following Practise Exercise
Practise Exercise 125 Further problems on fluid flow
1. If in the storage tank of worked Problem 2 on page 268, Figure 23.12, z1 = 8 m, determine the mass rate of flow from the outlet pipe.
[7.995 kg/s]
Impact of a jet on a stationary plate
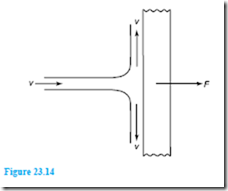
The impact of a jet on a plate is of importance in a number of engineering problems, including the determination of pressures on buildings subjected to gusts of wind.
Consider the jet of fluid acting on the flat plate of Figure 23.14, where it can be seen that the velocity of the fluid is turned through 90°, or change of velocity = v.
For wide surfaces, such as garden fences, the pressure can be calculated by the above formula, but for tall buildings and trees, civil engineers normally assume that:
Pressure p = 0.5 ρv2
This is because the flow of fluid is similar to the plan view shown in Figure 23.15, where the change of momentum is much less.
Problem 4. What would be the wind pressure of Problem 3, if the gale were acting on a very wide and flat surface?
Now try the following Practise Exercises
Practise Exercise 126 Further problems on the impact of jets on flat surfaces
1. A hurricane of velocity 220 km/h blows perpendicularly on to a very wide flat surface. Determine the wind pressure that acts on this surface due to this hurricane, when the density of air, ρ = 1.2 kg/m3. [0.0448 bar]
2. What is the wind pressure for Problem 1 on a slim, tall building? [0.0224 bar]
3. A tornado with a velocity of 320 km/h blows perpendicularly on to a very wide surface. Determine the wind pressure that acts on this surface due to this tornado, when the density of air, ρ = 1.23 kg/m3. [0.0972 bar]
4. What is the wind pressure for Problem 3 on a slim, tall building? [0.0486 bar]
5. If atmospheric pressure were 1.014 bar, what fraction of atmospheric pressure would be the wind pressure calculated in Problem 4?
Practise Exercise 127 Short-answer questions on the measurement of fluid flow
In the flowmeters listed 1 to 10, state typical practical applications of each.
1. Orifice plate.
2. Venturimeter.
3. Float and tapered-tube meter.
4. Electromagnetic flowmeter.
5. Pitot-static tube.
6. Hot-wire anemometer.
7. Turbine flowmeter.
8. Deflecting vane flowmeter.
9. Flow nozzles
9. Flow nozzles.
10. Rotary vane positive displacement meter.
11. Write down the relationship between the coefficients Cc, Cv and Cd
12. Write down the formula for the pressure due to a wind acting perpendicularly on a tall slender building.
Practise Exercise 128 Multiple-choice questions on the measurement of fluid flow
(Answers on page 298)
1. The term ‘flow rate’ usually refers to:
(a) mass flow rate
(b) velocity of flow
(c) volumetric flow rate
2. The most suitable method for measuring the velocity of high-speed gas flow in a duct is:
(a) venturimeter
(b) orifice plate
(c) Pitot-static tube
(d) float and tapered-tube meter
3. Which of the following statements is false?
When a fluid moves through a restriction in a pipe, the fluid
(a) accelerates and the pressure increases
(b) decelerates and the pressure decreases
(c) decelerates and the pressure increases
(d) accelerates and the pressure decreases
4. With an orifice plate in a pipeline the vena contracta is situated:
(a) downstream at the position of minimum cross-sectional area of flow
(b) upstream at the position of minimum cross-sectional area of flow
(c) downstream at the position of maximum cross-sectional area of flow
(d) upstream at the position of maximum cross-sectional area of flow
In Questions 5 to 14, select the most appropriate device for the particular requirements from the following list:
(a) orifice plate
(b) turbine flow meter
(c) flow nozzle
(d) pitometer
(e) venturimeter
(f) cup anemometer
(g) electromagnetic flow meter
(h) pitot-static tube
(i) float and tapered-tube meter
(j) hot-wire anemometer
(k) deflecting vane flow meter.
5. Easy to install, reasonably inexpensive, for
high-velocity flows.
6. To measure the flow rate of gas, incorporating a Wheatstone bridge circuit.
7. Very low flow rate of corrosive liquid in a chemical process.
8. To detect leakages from water mains.
9. To determine the flow rate of liquid metals without impeding its flow.
10. To measure the velocity of wind.
11. Constant flow rate, large bore pipe, in the general process industry.
12. To make a preliminary test of flow rate in order to specify permanent flow measuring equipment.
13. To determine the flow rate of fluid very accurately with low pressure loss.
14. To measure the flow rate of air in a ventilating duct.
15. For a certain wind velocity, what fraction of the pressure would act on a tall slender building in comparison with a very wide surface?
(a) 0.01
(b) 0
(c) 0.5
(d) 0.99
16. For a wind speed of 190 km/h, what fraction (approximate) of atmospheric pressure will this be, when blowing perpendicularly to a very wide surface?
(a) 2.5
(b) 0.5
(c) 1/30
(d) 0