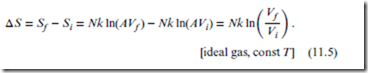Entropy & Ideal Gas
Measuring Our Molecular Ignorance
Our goals in this chapter are two-fold. First, we seek to prove that starting from the statistical, or information definition of S as presented in Equation (10.2), we can derive the thermodynamic form of Equation (10.1), under reversible conditions. As discussed in Chapter 10, the general proof is too advanced for the scope of this book. For the ideal gas, on the other hand, a simple and straightforward derivation is possible. For simplicity, we assume an ideal gas of point particles—although the derivation can easily be generalized to incorporate rotating molecules or those with other internal structure, provided that they are noninteracting.
The second goal is to use Equation (10.2) to derive an expression for the entropy state function, S, as an explicit function of the thermodynamic variables, (T, V ), for the ideal gas. We verify that the result is equivalent to the famous Sackur-Tetrode equation [Equation (11.11), p. 93] to within an
additive constant. This again confirms the agreement of the two entropies, for the ideal gas case. In this fashion, we establish a connection between the statistical and thermodynamic definitions of entropy, using the information theory approach.
⊳⊳⊳ Helpful Hint: When working with S as a state function, the natural thermodynamic variables are T and V , for reasons described below. See Section 9.2 for a discussion of natural variables, and Section 14.1 for a more formal discussion of “conjugate variables.”
It all boils down to counting states properly—i.e., to the calculation of Ω.
For an ideal gas of point particles, the molecular state of the whole system is specified via the 6N molecular coordinates, (xi , yi , zi ) and (vx,i, vy,i, vz,i ). As macroscopic observers, we do have some a priori information about the values of these 6N coordinates, but our knowledge is incomplete. Our lack of knowledge about the particle positions is directly associated with the sys- tem volume, V . Likewise, our lack of knowledge about the particle velocities (and kinetic energies) is associated with the temperature, T. These two sources of “ignorance” both contribute to the total entropy of a given ther- modynamic state, (T, V ), and can be treated separately.
As discussed in Section 10.4, Ω is enormous—even infinite, ina sense, as we will see. For non-ideal systems, intermolecular interactions make the calculation of Ω difficult. The calculation becomes much simpler in the ideal gas case because the individual particles are statistically independent. Thus, as per Section 10.3, Ω can be obtained directly from Ω1 (the number of states available to a single particle) via
It remains only to determine Ω1, in terms of the available single-particle positions, (x, y, z), and velocities, (vx, vy, vz)—where the ‘i’ subscripts are henceforth dropped (see Section 6.2).
Volume Contribution to Entropy
Consider the change in entropy, ΔS, brought about via isothermal (true) expansion of the ideal gas. Because T is fixed, there is no change in the (statistically-averaged) particle velocities. Therefore, all of ΔS is due to the increase in volume, which in turn is associated with changes in the particle positions.
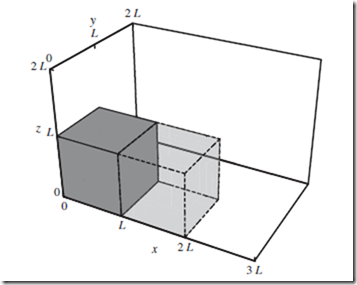
Now consider the physical box within which the system resides, as depicted in Figure 11.1. As macroscopic observers, we know that every particle must lie somewhere inside the box, but we have no idea precisely where.
Thus, if a measurement of a given particle’s position were to be performed, we know a priori that there would be zero probability of finding the particle outside the box, and equal probability of finding it at any point inside the box.
Figure 11.1 Expansion of a cubical box. Cubical box of volume V = L3 (opaque gray, solid lines), denoting physical limits of the system. Without performing an explicit measurement of precise particle positions, we know that such a measurement would find every particle to be inside rather than outside, of the cube. This knowledge provides partial a priori information about the molecular state. Under
expansion of the box out to x = 2L, (translucent gray, dashed lines), our knowledge of the particle positions decreases, and the entropy accordingly increases.
⊳⊳⊳ To Ponder… Although it is convenient to think of entropy as the amount of information gained by the observer as a result of precise particle measurement, it is important to realize that such a measurement is imagined to be hypothetical only. The reality is that modern science actually does enable us to peer at individual molecules, in a manner that would have been inconceivable to the founding fathers of thermodynamics. In that sense, we are no longer true macroscopic observers.
It is natural to think of each (x, y, z) point as constituting a different “position state” for a single particle. The total number of position states available to a given particle is thus equal to the number of points inside the box. Since space is continuous, this number is technically infinite. However, that is not too problematic, since (as we will see) the determination of ΔS requires only the relative number of available states. In any case, it is evident that the number of points inside the box—and therefore Ω1 (at constant T)—is proportional to the box volume, V . We thus have
where A remains constant under isothermal expansion. In principle, A can depend on T, but it must be independent of V .
From Equations (10.2), (11.1), and (11.2), we thus find
For macroscopic systems, Ω= (AV )N grows enormously quickly with V . However, the logarithm converts the exponent into a linear N factor. Thus, entropy is extensive, as it should be. In the ideal gas case, the extensivity of S follows from the additivity of information for independent measurements (Section 10.3).
Equation (11.4) is a quantitative prediction, with no unspecified parameters, for the change in entropy of an ideal gas under isothermal doubling of the volume. Note that in the final expression for ΔS, the actual values of Ωi and Ωf do not appear. In general, all that matters for entropy change is the ratio, (Ωf ∕Ωi). Note also that ΔS > 0, as expected.
More generally, if the volume change is arbitrary (i.e., from any Vi to any Vf ), but still isothermal,
Again, the actual volume values do not matter for ΔS; only the ratio of final to initial volumes is relevant. Nor does the unspecified constant A enter into the final form for ΔS. Consequently, a specific numerical prediction can be made for the ΔS value for any isothermal gas expansion.
Temperature Contribution to Entropy
Thus far, we have considered only changes in V at constant T. To round out the full thermodynamic story, we must also consider changes in T at constant V . Because V is fixed, there is no change in our information about the molecular positions; these therefore play no role in the origin of ΔS in this case. The entropy does change, however—owing to a change in the available velocity states, induced by the change in temperature.
⊳⊳⊳Helpful Hint: Remember: V corresponds to the avail- able molecular positions; T corresponds to the available molecular velocities.
Recall from Section 6.2 that for a system in thermal equilibrium, the distribution of particle velocities is not uniform, but adheres to the Maxwell- Boltzmann distribution [Equation (6.2) and Figure 6.1]. Recall, also, that this same distribution describes all three velocity components of all system particles—although for simplicity, we refer to a single, ‘vx’ component only.
⊳⊳⊳ To Ponder… Why can’t we use the Maxwell distribution of speeds [Equation (6.6)] instead of the Maxwell- Boltzmann distribution? Because it is based on speeds v, rather than velocities (vx, vy, vz), and therefore does not incorporate complete molecular state information [some of the velocity information is lost in Equation (6.6)—namely, the directional information].
For a given velocity component of a given particle, we need to somehow estimate the number of available states associated with the Equation (6.2) distribution. The way that we do this is by defining an “effective” range of allowed vx values. We can then use this range as a measure of the number of available vx states—just like we did in Section 11.2 for the position states. In both cases, the bigger the (effective) range, the greater the number of available states.
From Section 6.2, we learn that the standard deviation, vx , is a good measure of the effective range of the vx distribution. For the Maxwell- Boltzmann distribution, in particular, the standard deviation—and hence, the number of available vx states—is found to increase proportionally with the square root of the temperature (i.e., vx ∝ T [Equation (6.5)]). Since there are three velocity components for each particle, each of which is independent of the other two, the total number of (vx, vy, vz) velocity states avail- able to each particle must be proportional to T1∕2 × T1∕2 × T1∕2 = T3∕2.
In this manner, we are led to
Like the last part of Equation (11.3), the new form of the ideal gas entropy as given by Equation (11.7) also depends on an unspecified quantity— in this case B. Once again, however, an unambiguous prediction can be obtained for ΔS (now under constant volume conditions) with no unspecified parameters:
Combined Entropy Expression
Comparing the rightmost parts of Equations (11.3) and (11.7), we find that A(T)V = T3∕2B(V ). This can only be true if A(T) = CT 3∕2 and B(V ) = CV , where C is a true thermodynamic constant. This means that C depends neither on T nor V , and is therefore independent of the thermodynamic state. We thus obtain
i.e., the desired explicit S(T, V ) state function for the ideal gas.
Note that in Equation (11.9) above, the value of the constant C is still unspecified. This means that the above analysis is insufficient to provide us with absolute entropy values—i.e., specific numerical values for S(T, V ) itself—though it does specify S(T, V ) to within an additive constant. Nevertheless, C is indeed found to have a specific value in nature, which can be determined using quantum mechanics (a discipline that lies outside the scope of this book).
⊳⊳⊳ To Ponder…at a deeper level. As discussed, classical theory technically predicts an infinite value for C, because the number of available states, Ω, is infinite. According to quantum theory, on the other hand, the uncertainty principle effectively “quantizes” the continuous classical molecular states, thus replacing them with a finite number of discrete quantum states. In this way, the “infinite states” difficulty of Section 11.2 is avoided.
For reference, we provide the quantum mechanical value of C; it is
where e is the Euler constant, and h is Planck’s constant. Substitution of Equation (11.10) into Equation (11.9) then leads exactly (after incorporating a correction due to the indistinguishability of quantum particles) to the Sackur-Tetrode equation:
⊳⊳⊳ Helpful Hint: Whenever h or ℏ appears in a formula, you know that quantum mechanics is somehow involved.
⊳⊳⊳Helpful Hint: Some authors write the Sackur-Tetrode equation in a form that—unlike Equation (11.11), and the second Helpful Hint in the Log Blog post on p. 63—does not use dimensionless logarithm arguments. This situation arises because the logarithm contribution is split into two or more separate terms. When using such a form to solve problems, you must be extremely careful with units.
Although C remains unspecified in a purely classical analysis, its value is immaterial insofar as entropy change is concerned. This is because C— being a multiplicative factor within the logarithm argument of Equation (11.9)—is converted into an additive constant, which must cancel out in any calculation of ΔS. This can be seen more explicitly as follows:
Due to a cancellation of factors, C does not appear in the final expression above. A more suggestive form of this same equation—valid for arbitrary thermodynamic changes—is provided below:
Note from Equation (11.13) that ΔS separates cleanly into additive “volume entropy” and “temperature entropy” contributions, each of which involves a logarithm with a dimensionless argument. These two contributions are associated, respectively, with changes in our knowledge about the particle positions and velocities. Note also that Equation (11.13) reduces to Equation (11.5) in the special case of constant T changes, and to Equation (11.8) for constant V changes.
Entropy, Heat, & Reversible Adiabatic Expansion
We now derive the well-known relation between entropy and heat, under reversible infinitesimal changes of state—i.e., Equation (10.1). Although this differential relation is true even for non-ideal systems, our proof encompasses only the ideal gas case.
⊳⊳⊳Helpful Hint: You should be aware that there is a tendency among many authors to express the heat absorbed under reversible conditions as if it were its own special quantity—the reversible heat, Qrev. We do not regard this
to be a thermodynamic quantity in its own right; in reality, this is just the usual heat Q, but restricted to reversible thermodynamic processes only. Similar comments apply to reversible work (Section 8.4, p. 60).
From Equations (9.16) and (11.9), the total differential dS for the state function S(T, V ) is
which is identical to Equation (10.1).
The relation between heat and entropy has important ramifications for reversible adiabatic expansions (see Chapters 13 and 16). For most thermodynamic quantities, this is the hardest special case because it involves changes in all three thermodynamic variables, T, P, and V . A student might therefore be well inclined to panic at the prospect of having to work out how a tricky quantity such as entropy might change under a reversible adiabatic expansion! In fact, though, this calculation could not be easier; under these
conditions, dQ = 0, and so Equation (11.16) implies that ΔS = 0. This is a general result, true for non-ideal as well as ideal gases, so It’s OK to be Lazy. The information ramifications of ΔS being zero under a reversible adiabatic change are interesting to consider. Under these conditions, Ω remains constant, and thus the total amount of information that we have about the system remains unchanged. On the other hand, this does not imply that the actual molecular states that are available to the system themselves remain the same. Instead, Equation (11.13) implies that the increase in volume entropy must be exactly balanced by a corresponding decrease in temperature entropy.
⊳⊳⊳ To Ponder…at a deeper level. In effect, we gain information about the particle velocities, while simultaneously losing information about their positions, in a kind of “thermodynamic uncertainty principle.”