Perpetual Motion Engines
Perpetual motion engines are engines that violate the first or the second law of thermodynamics, or both. Naturally, one will never meet these engines since they are impossible to build—the thermodynamic laws are not to be violated! One might meet inventors, however, who claim to have invented engines that do miraculous things. Inevitably, the inventors will never be able to show their engines in working condition, and their claims remain eternally unproven.
A perpetual motion engine of the first kind is an engine that violates the first law of thermodynamics, e.g., an engine that produces more work than the net heat exchange 
A perpetual motion engine of the second kind is an engine that violates the second law of thermodynamics, e.g., a heat engine operating between two reservoirs at TL, TH with an efficiency above the Carnot efficiency, η > 1− TL .
Violations of the second law are sometimes difficult to understand, and thus perpetual motion engines of the second kind are more difficult to identify for not so clever inventors, and their gullible investors.
Reversible and Irreversible Processes
Irreversible processes are associated with entropy generation which reduces the performance of engines. So far the terms reversible and irreversible were rather loosely defined in Sec. 2.10. A more exact definition of these terms will make it easier to identify irreversible processes, and the related losses. We define:
A thermodynamic process from state 1 to state 2 is reversible, if the process can be inverted so that the system returns to its initial state (state 1), and no changes remain in its surroundings.
A thermodynamic process from state 1 to state 2 is irreversible, if, when the system is brought back into its initial state (state 1), changes remain in its surroundings.
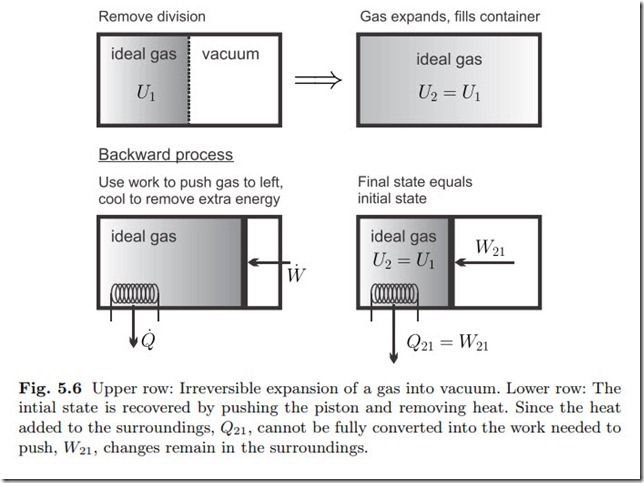
For an example, we return to the uncontrolled expansion of an ideal gas, which is shown again in Fig. 5.6. We found, in Sec. 3.13, that the internal energies of initial and final states are the same, U2 = U1, while the gas fills a bigger volume in the final state, V2 > V1. To return the gas to the initial state, its volume must be reduced by compression, which requires the (reversible) work 
The first law for any process from state 2 back to the initial state 1 reads
so that the heat Q21 = W21 < 0 must be removed from the system, as shown in the figure. Thus, the process 2-1 draws the work W21 from the surroundings and transfers the heat Q21 to the surroundings. The process would be reversible, if the heat Q21 could be completely converted to the work W21 by an engine residing in the surroundings. This, however, is forbidden by the Kelvin-Planck statement of the second law, which states that only some of the heat can be converted to work, but not all. Thus, some extra work has to be provided to return the system to its original state, the system’s surroundings have changed: the original process is irreversible.
Heat transfer serves as another example: The heat |QAB | has flown from a hot body A to a cold body B by itself. To return both bodies to their original state one can use a heat pump, which consumes the work WHP , removes the heat QAB from the colder body B, and delivers the heat |QI | = |QAB |+|WHP | to the warmer body A. After this, body B is in its initial state.
Body A received too much heat, however. To return A into its initial state, the heat |QII | = |WHP | must be moved from A to the surroundings. Due to the Kelvin-Planck statement, the heat added to the surroundings |QII | can only provide part of the work | process is irreversible.