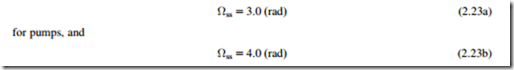Cavitation
Cavitation is the boiling of a liquid at normal temperature when the static pressure is made sufficiently low. It may occur at the entry to pumps or at the exit from hydraulic turbines in the vicinity of the moving blades. The dynamic action of the rotor blades causes the static pressure to reduce locally in a region that is already normally below atmospheric pressure and cavitation can commence. The phenomenon is accentuated by the presence of dissolved gases that are released with a reduction in pressure.
For the purpose of illustration, consider a centrifugal pump operating at constant speed and capacity. By steadily reducing the inlet pressure head, a point is reached when streams of small vapor bub- bles appear within the liquid and close to solid surfaces. This is called cavitation inception and commences in the regions of lowest pressure. These bubbles are swept into regions of higher pressure where they collapse. This condensation occurs suddenly, the liquid surrounding the bubbles either hit- ting the walls or adjacent liquid. The pressure wave produced by bubble collapse (with a magnitude on the order of 400 MPa) momentarily raises the pressure level in the vicinity and the action ceases. The cycle then repeats itself and the frequency may be as high as 25 kHz (Shepherd, 1956). The repeated action of bubbles collapsing near solid surfaces leads to the well-known cavitation erosion.
The collapse of vapor cavities generates noise over a wide range of frequencies—up to 1 MHz has been measured (Pearsall, 1972), i.e., so-called white noise. Apparently the collapsing smaller bubbles cause the higher frequency noise, and the larger cavities the lower frequency noise. Noise measurement can be used as a means of detecting cavitation (Pearsall, 1967). Pearsall and McNulty (1968) have shown experimentally that there is a relationship between cavitation noise levels and erosion damage on cylinders and conclude that a technique could be developed for predicting the occurrence of erosion.
Up to this point, no detectable deterioration in performance occurs. However, with further reduction in inlet pressure, the bubbles increase both in size and number, coalescing into pockets of vapor that affects the whole field of flow. This growth of vapor cavities is usually accompanied by a sharp drop in pump performance as shown conclusively in Figure 2.2 (for the 5000 rpm test data). It may seem surprising to learn that, with this large change in bubble size, the solid surfaces are much less likely to be damaged than at inception of cavitation. The avoidance of cavitation inception in conventionally designed machines can be regarded as one of the essential tasks of both pump and turbine designers. However, in certain recent specialized applications, pumps have been designed to operate under supercavitating conditions. Under these conditions, large size vapor bubbles are formed, but bubble collapse takes place downstream of the impeller blades. An example of the specialized application of a supercavitating pump is the fuel pumps of rocket engines for space vehicles, where size and mass must be kept low at all costs. Pearsall (1973) has shown that the supercavitating principle is most suitable for axial flow pumps of high specific speed and has suggested a design technique using methods similar to those employed for conventional pumps.
Pearsall (1973) was one of the first to show that operating in the supercavitating regime was practicable for axial flow pumps, and he proposed a design technique to enable this mode of opera- tion to be used. A detailed description was published in Pearsall (1972), and the cavitation performance was claimed to be much better than that of conventional pumps. Some further details are given in Chapter 7.
Cavitation limits
In theory, cavitation commences in a liquid when the static pressure is reduced to the vapor pressure corresponding to the liquid’s temperature. However, in practice, the physical state of the liquid will determine the pressure at which cavitation starts (Pearsall, 1972). Dissolved gases come out of solution as the pressure is reduced, forming gas cavities at pressures in excess of the vapor pressure. Vapor cavitation requires the presence of nuclei—submicroscopic gas bubbles or solid non- wetted particles—in sufficient numbers. It is an interesting fact that in the absence of such nuclei, a liquid can withstand negative pressures (i.e., tensile stresses)! Perhaps the earliest demonstration of this phenomenon was that performed by Reynolds (1882) before a learned society. He showed how a column of mercury more than twice the height of the barometer could be (and was) supported by the internal cohesion (stress) of the liquid. More recently Ryley (1980) devised a simple centrifugal apparatus for students to test the tensile strength of both plain, untreated tap water in comparison with water that had been filtered and then deaerated by boiling. Young (1989) gives an extensive literature list covering many aspects of cavitation including the tensile strength of liquids. At room temperature, the theoretical tensile strength of water is quoted as being as high as 1000 atm (100 MPa)! Special pretreatment (i.e., rigorous filtration and pre-pressurization) of the liquid is required to obtain this state. In general, the liquids flowing through turbomachines will contain some dust and dissolved gases and under these conditions negative pressure does not arise.
A useful parameter is the available suction head at entry to a pump or at exit from a turbine. This is usually referred to as the net positive suction head, NPSH, defined as
where po and pv are the absolute stagnation and vapor pressures, respectively, at pump inlet or at turbine outlet.
To take into account the effects of cavitation, the performance laws of a hydraulic turbomachine should include the additional independent variable Hs. Ignoring the effects of Reynolds number, the performance laws of a constant geometry hydraulic turbomachine are then dependent on two groups of variable. Thus, the efficiency,
It is known from experiments made by Wislicenus (1965) that cavitation inception occurs for an almost constant value of Ωss for all pumps (and, separately, for all turbines) designed to resist cavitation. This is because the blade sections at the inlet to these pumps are broadly similar (likewise, the exit blade sections of turbines are similar) and the shape of the low-pressure passages influences the onset of cavitation.
Using the alternative definition of suction specific speed Ωss 5 ΩQ1/2/(gHs)3/4, where Ω is the rotational speed in rad/s, Q is the volume flow in m3/s, and gHs is in m2/s2. Wislicenus showed that
Pearsall (1967) describes a supercavitating pump with a cavitation performance much better than that of conventional pumps. For this pump, suction specific speeds Ωss up to 9.0 were readily obtained and, it was claimed, even better values might be possible but at the cost of reduced head and efficiency. It is likely that supercavitating pumps will be increasingly used in the search for higher speeds, smaller sizes, and lower costs.