Basic Electricity:Electrical Quantities and Ohm’s Law

Electrical Quantities and Ohm’s Law

Electricity has a standard set of values. Before you can work with electricity, you must have a knowledge of these values and how to use them. Because the values of electrical measurement have been standardized, they are understood by everyone who uses them. For instance, carpenters use a standard system for mea- suring length, such as the inch or foot. Imagine what a house would look like that was constructed by two carpenters who used different lengths of measure for an inch or foot. The same holds true for people who work with electricity. A volt, ampere, or ohm is the same for everyone who uses them.

COULOMB

A coulomb is a quantity measurement of elec- trons. One coulomb contains 6.25 X 1018 electrons. The number shown in Figure 2–1 is the number of

6,250,000,000,000,000,000

Figure 2–1

The number of electrons in a coulomb. (Source: Delmar/Cengage Learning)

electrons in one coulomb. Because the coulomb is a unit of measurement, it is similar to a quart, gallon, or liter. It takes a certain amount of liquid to equal a quart, just as it takes a certain amount of electrons to equal a coulomb.

AMPERE

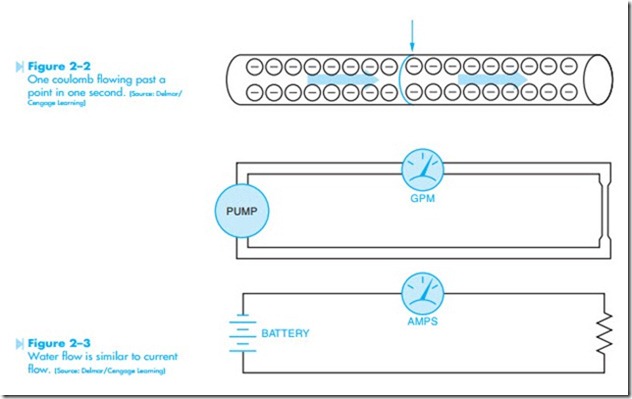
The ampere, or amp, is defined as one coulomb per second. Notice that the definition of an amp involves a quantity measurement (the coulomb) combined with a time measurement (the second). One amp of current flows through a conductor when one coulomb flows past a point on one second, Figure 2–2. Amperage is a measurement of the actual amount of electricity that is flowing through a circuit. In a water system, it would be comparable to gallons per minute or gallons per second, Figure 2–3. If one coulomb were to flow past a point in a half second, there would be 2 amperes of current flow. If one coulomb were to flow past a point in two sec- onds there would be a half amp of flow. Current is normally measured in amperes, milliamperes, and microamperes. A milliamp is one-thousandth of an amp (0.001). A microamp is one-millionth of an amp (0.000,001).

VOLT

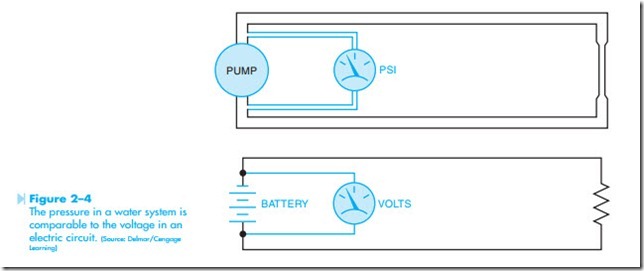
Voltage is actually defined as electromotive force, or EMF. It is the force that pushes the electrons through a wire and is often referred to as electrical pressure. One should remember that voltage cannot flow. To say that voltage flows is like saying that pressure flows through a pipe. Pressure can push water through a pipe, and it is correct to say that water flows through a pipe, but it is not correct to say that pressure flows through a pipe. The same is true for voltage. The voltage pushes current through a wire, but voltage cannot flow through a wire. In a water system, the voltage could be com- pared to the pressure of the system, Figure 2–4.

OHM

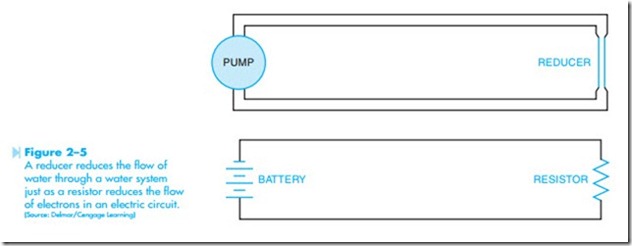
The ohm is the measure of the resistance to the flow of current. The voltage of the circuit must over- come the resistance before it can cause electrons to flow through it. Without resistance, every electrical circuit would be a short circuit. All electrical loads, such as heating elements, lamps, motors, transformers, and so forth, are measured in ohms. In a water system, a reducer would be used to control the flow of water. In an electrical circuit, a resistor can be used to control the flow of electrons. Figure 2–5 illustrates this concept.

There are electrical quantities other than resistance that are also measured in ohms. Inductive reactance and capacitive reactance are current-limiting forces that exist in alternating current circuits and will be discussed later in the text. Another term used to describe a current-limiting force is impedance. Impedance is a combination of all current limiting forces in a circuit and can include resistance, inductive reactance, and capacitive reactance. Because resistance is only one of the current-limiting forces found in alternating current circuits, impedance is the quantity generally used to describe the current- limiting force in an alternating current circuit. Imped- ance will be discussed in more detail later in the text.

WATT

Wattage is a measure of the amount of power that is being used in the circuit. It is proportional to the amount of voltage and the amount of current flow.

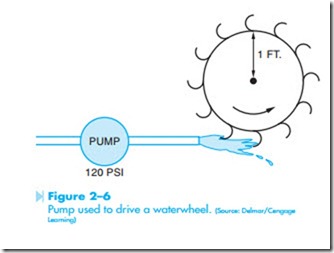
To understand watts, return to the example of the water system. Assume that a water pump has a pressure of 120 psi (pounds per square inch) and causes a flow rate of one gallon per second. Now assume that this water is used to drive a waterwheel as shown in Figure 2–6. Notice that the waterwheel has a radius of 1 ft from the center shaft to the rim of the wheel. Since water weighs 8.34 pounds per gallon, and is being forced against the wheel at a pressure of 120 psi, the wheel could develop a torque of 1000.8 foot pounds (120 X 8.34 X 1 = 1000.8). If the pressure is increased to 240 psi, but the water flow remains constant, the force against the wheel will double (240 X 8.34 X 1 = 2001.6). If the pressure remains at 120 psi, but the water flow is increased to two gallons per second, the force against the wheel will again double (120 X 16.68 X 1 = 2001.6). Notice that the amount of power developed by the waterwheel is determined by both the amount of pressure driving the water and the amount of flow.

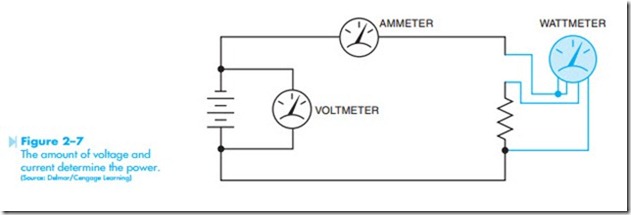
The power of an electrical circuit is very similar. Figure 2–7 shows a resistor connected to a circuit with a voltage of 120 volts and a current flow of 1 amp. The resistor shown represents an electric heating element. When 120 volts forces a current of 1 amp through it, the heating element will produce 120 watts of heat (120 X 1 = 120 watts). If the volt- age is increased to 240 volts, but the current remains constant, the element will produce 240 watts of heat (240 X 1 = 240 watts). If the voltage remains at 120 volts, but the current is increased to 2 amps, the heating element will again produce 240 watts (120 X 2 = 240). Notice that the amount of power used by the heating element is determined by the amount of current flow and the voltage driving it.

A good rule to remember concerning watts, or true power, is that before watts can exist in an electric circuit, electrical energy must be converted or changed into some other form. When current flows through a resistor, the resistor becomes hot and dissipates heat. Heat is a form of energy. The wattmeter connected in the circuit shown in Figure 2–7 mea- sures the amount of electrical energy that is being converted into heat energy. If the resistor shown in Figure 2–7 were replaced with an electric motor the wattmeter would measure the amount of electrical energy that was converted into mechanical energy.

OHM’S LAW

Ohm’s law is named for the German scientist George S. Ohm. Ohm discovered that all electrical quantities are proportional to each other and can therefore be expressed as mathematical formulas. In its simplest form, Ohm’s law states that it takes 1 volt to push 1 amp through 1 ohm.

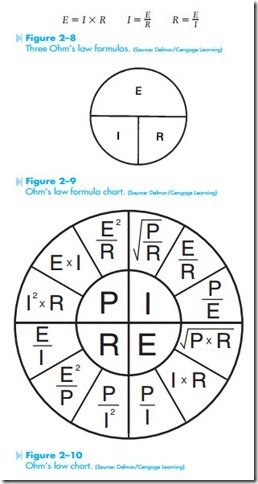
Figure 2–8 shows three basic Ohm’s law formulas.

In these formulas, E stands for electromotive force and is used to represent the voltage. The I stands for the intensity of the current and is used to represent the amount of current flow or amps. The letter R stands for resistance and is used to represent the ohms.

The first formula states that the voltage can be found if the current and resistance are known. Volt- age is equal to amps multiplied by ohms. For example, assume a circuit has a resistance of 50 ohms and a current flow through it of 2 amps. The voltage con- nected to this circuit is 100 volts (2 amps X 50 ohms = 100 volts). The second formula indicates that if the voltage and resistance of the circuit are known, the amount of current flow can be found. Assume a 120-volt circuit is connected to a resistance of 30 ohms. The amount of current that will flow in the circuit is 4 amps (120 volts/30 ohms = 4 amps). The third formula states that if the voltage and cur- rent flow in a circuit are known, the resistance can be found. Assume a circuit has a voltage of 240 volts and a current flow of 10 amps. The resistance in the circuit is 24 ohms (240 volts/10 amps = 24 ohms).

Three Ohm’s law formulas. (Source: Delmar/Cengage Learning)

Figure 2–9 shows a simple chart that can be a great help when trying to remember the Ohm’s law formula. To use the chart, cover the quantity to be found. For example, if the voltage, E, is to be found, cover the E on the chart. The chart now shows the remaining letters IR. Therefore, E = I X R. If the current is to be found, cover the I on the chart. The chart now shows

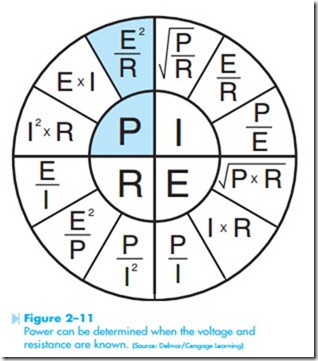
A larger chart that shows the formulas needed to find watts as well as the voltage, amperage, and resistance is shown in Figure 2–10. Because watt is the unit of electric power, the letter P is used to represent watts. The chart is divided into four quadrants. Each quadrant contains three formulas that can be used to find the electrical quantity rep- resented in that quadrant.

EXAMPLE 1: An electric heating element is connected to 120 volts and has a resistance of 18 ohms. What is the power consumption of this element?

SOLUTION: The electrical quantity to be determined is power, or watts. The known electrical values are voltage and resistance. Using the formula chart

Figure 2–10, choose the formula for finding power that includes the two known electrical quantities. The formulas for determining power are located in the first quadrant of the chart. The formula that contains the known values of voltage and resistance is P = E2/R, as shown in Figure 2–11.

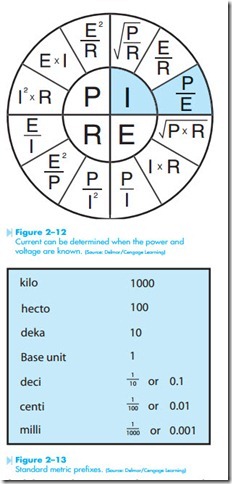
Current can be determined when the power and voltage are known. (Source: Delmar/Cengage Learning) EXAMPLE 2: A 240-volt electric furnace has a power rating of 15,000 watts, or 15 kW. How much cur- rent will this furnace draw when in operation?

SOLUTION: The quantity you are looking for is cur- rent or amps, represented by the letter I.

Formulas for determining current are located in the second quadrant of the formula chart shown in Figure 2–10. The two known quantities are power (watts) and voltage. The correct formula is I = P/E, as shown in Figure 2–12.

METRIC PREFIXES

Metric prefixes are used in the electrical field just as they are in most other scientific fields. In the English system of measure, different divisions are used for different measurements. A yard, for example, can be divided into 3 feet. A foot is generally divided into 12 inches, and an inch is often divided into sixteenths. In the metric system, ten or a multiple of ten is always the dividing factor. A kilometer can be

divided into 10 hectometers. A hectometer can be divided into 10 dekameters, and a dekameter can be divided into 10 meters. A chart listing standard metric prefixes is shown in Figure 2–13.

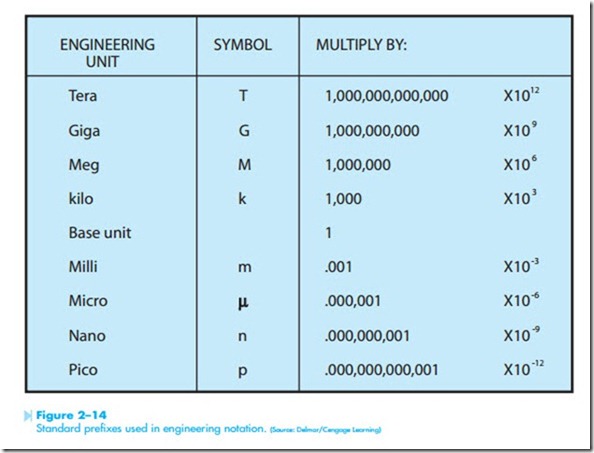
In the electrical field, a different type of metric notation called engineering notation is used instead of the standard metric prefixes. Engineering notation is in steps of one thousand instead of ten. A chart listing common engineering notation prefixes and their symbols is shown in Figure 2–14. Starting with the base unit or one, the first engineering unit greater than one is kilo, or one thousand. The next engineering unit greater than kilo is Mega, or one million. A million is one thousand times larger than a thousand. The first engineering unit less than the base unit is milli, or one one thousandth. The next engineering unit less than milli is micro, or one one- millionth. A millionth is one thousand times smaller than a thousandth.

These prefixes are used to simplify standard electrical measurements. Five billion watts can be writ- ten as 5,000,000,000 W or as 5 GW. Twenty-five microamperes can be written as 0.000,025 A or as 25 μA.