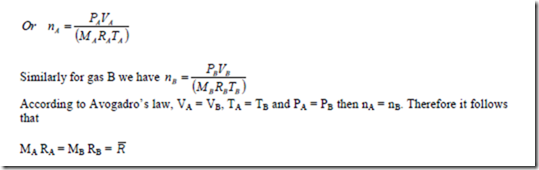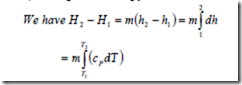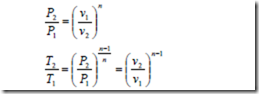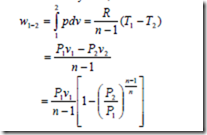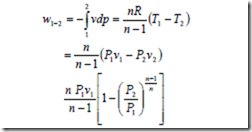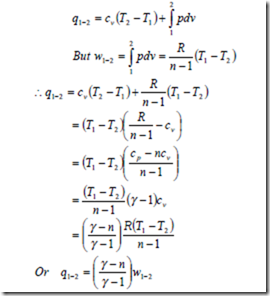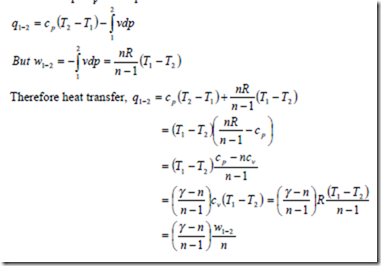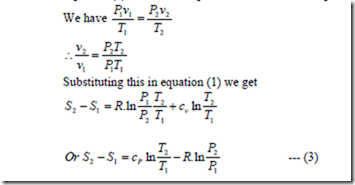Ideal Gas
Definition: A substance is said to be an ideal gas if it satisfies the following equations i.e., Pv = RT and u = f (T)
Where P is the pressure exerted by the substance, v is the specific volume of the substance, T is the temperature in degree Kelvin, u is the specific internal energy and R is the gas constant. Experience has shown that almost all real gases satisfy the above equations over wide ranges of pressures and temperatures. However there are certain situations where the real gases cannot be treated as ideal gases.
Mole of a Gas
A mole of a gas is that quantity of gas whose mass is numerically equal to its molecular weight.
For example, 1 kg mol of hydrogen is equal to 2 kg, has molecular weight of hydrogen is 2. Therefore if n is the total number of moles, m is mass and M is the molecular weight then, nM=m
Avogadro’s Hypothesis
Avogadro’s law states that equal volumes of all gases measured at the same temperature and pressure contain the same number of moles.
Consider two gases A and B. The law states that if VA = VB, TA = TB and PA = PB then nA = nB For gas A, the equation of state can be written as PA VA = mA RA TA = nA MA RA TA
Where R is called the universal gas constant and R is called the characteristic gas constant. The value of R =8.3143 kJ/kgmol-K.
The ideal gas equation can also be written in terms of R as pV = nMRT = n R T where R = R/M
Specific Heat of Ideal Gases
From the definition of specific heat at constant volume and the specific heat at constant pressure, we have
To integrate the above equation we should know the functional relationship between cV and dT. A perfect gas equation is one for which cv is a constant.
Therefore, U2-U1= m cv (T2 – T1)
ii) Change in Enthalpy
For a perfect gas cP is constant. Therefore the above equation can be integrated and we get H2-H1= m cP (T2 – T1)
Work done by a perfect gas during a reversible adiabatic process in a closed system:
From the first law of TD,
dq = du + dw
For an adiabatic process, δq=0
Hence the work done by a unit mass of a perfect gas on a piston during an adiabatic expansion process is equal to the decrease in internal energy, i.e., δw = -du
Whereas, for an adiabatic compression process, the internal energy of the gas will increase with a consequent increase in temperature.
Work done by a perfect gas during a reversible adiabatic Steady Flow process:
Neglecting the effect of changes in velocity and elevation, SFEE for a unit mass of fluid is given by q1-2 – w1-2 = Dh
Since the process is adiabatic, q=0. Hence work done per unit mass of a perfect gas during an adiabatic steady flow expansion process is equal to the decrease in enthalpy, i.e.,w1-2 = h1-h2
For a perfect gas, dh = cpdT
It may be noted that the work done for a steady flow system is g times that for a closed system.
Note: The above equations may be derived for reversible processes by taking integral p dv for closed system and taking integral of minus v dp for a steady flow system with negligible changes in the kinetic and potential energies from the initial to the final state.
The polytropic process of a perfect gas: A Polytropic process is one for which the pressure volume relation is given by pvn = constant, where the exponent n for the given process is a constant and may have any numerical value ranging from plus infinity to minus infinity.
From the above equation, it is evident that the properties at the end states of the reversible or irreversible polytropic process of a perfect gas may be written in the form
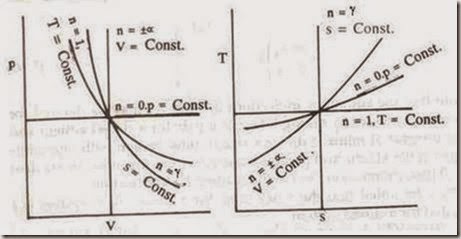
There are four values of the exponent n that indicate processes of particular interest. When
-
n = 0, constant pressure or isobaric process
-
n = ± ∞, constant volume or isovolumic process
-
n = 1, constant temperature or isothermal process and
-
n = g, constant entropy or isentropic process
These processes are shown in the fig. on p-v and T-s diagrams.
Figure: Polytropic Process on p-v and T-s diagrams
Work done and heat transfer by a perfect gas during a polytropic process:
For the closed system, the work done during a polytropic expansion process is given by,
The work done for a steady flow system during a polytropic expansion process is given by,
It may be noted that the work done for a steady flow system is n times that for a closed system.
i) The heat transfer for a closed system:
From the first law of thermodynamics for a unit mass of substance
δq = δw + du
Since du = cvdT and for a reversible process δw = pdv δq = cvdT + pdv
Therefore heat transfer per unit mass during a polytropic process in a closed system from the initial state to final state is given by
ii) The heat transfer in a steady flow process:
From the first law for steady flow system for a unit mass of fluid
δq = δw + dh
But dh = cpdT and for a reversible steady flow process δw = -vdp
Therefore δq = cpdT – vdp
Change in Entropy
Let P1, v1, T1, S1 apply to the initial conditions of certain amount of gas. P2, v2, T2, S2, apply to the final conditions after adding some heat.
Equation (1) can also be express in terms of pressure and volume.
Evaluation of change in entropy in various quasi static processes
1. Constant Volume Process
Related posts:
Incoming search terms:
- t-s p-v diagrams
- all processes on ts diagram
- reversible adiabatic expansion example
- pv and ts diagram of polytropic process
- polytropic process work equation
- polytropic process real gas
- polytropic process on p-v and t-s diagram
- polytropic process heat transfer
- machineryequipmentonline/hvac-machinery/real-gases/
- flow process of perfect gases
- temperature entropy diagram polytropic