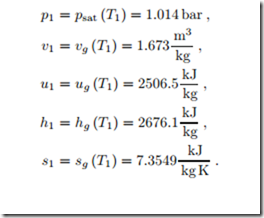Superheated Vapor
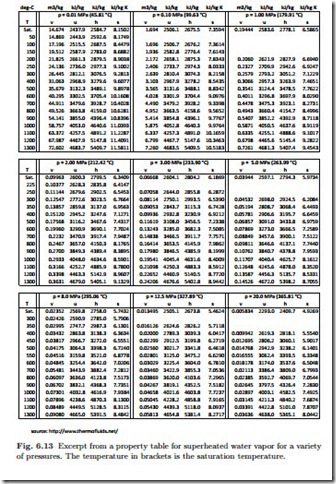
For superheated vapors the equations of state depend on two properties, and are normally laid down in extensive tables, or in computer software. Figure 6.13 shows an excerpt of a table with data for water vapor at some pressures between 10 kPa and 20 MPa.
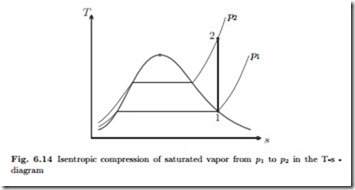
As an example we consider the adiabatic reversible compression of satu- rated vapor at T1 = 100 ◦C to a pressure p2 = 3 MPa. From the second law for reversible processes, δq = T ds follows that such a process is isentropic (constant entropy), and thus it is a natural choice to draw the process curve in a T-s-diagram as depicted in Fig. 6.14. Clearly, the final state 2 is outside the two phase region, to the right, which means the final state is superheated vapor. The properties of state 1 can be read from the saturation table in Fig. 6.10 as
Two bits of information are required to identify state 2, and here these are its pressure, p2, and its entropy, since the process is isentropic, s2 = s1 = 7.3549 kJ . In the table for superheated water vapor, Fig. 6.13, we have to consider the center box which refers to the pressure 3 MPa. The required value for entropy cannot be found in the table, but lies between values given.
The values closest above and below the required value of s2 = 7.3549 kJ in the table are
Here, va = v (p2, Ta), ua = u (p2, Ta) etc. are the appropriate data values from the table.
Since the process is adiabatic, we have q12 = 0 and the work per unit mass can be computed from the first law as w12 = u1 − u2 + q12 = −679.5 kJ .
Thermodynamic properties are often listed in tables as discrete values, and interpolation must be frequently used. Typically, tabulated values are spaced such that the assumption of linearity is valid in good approximation.