Ac transformers are one of the keys to allowing widespread distribution of electric power as we see it today. Transformers efficiently convert electricity to higher voltage for long distance transmission and back down to low voltages suitable for customer usage. The distribution transformer normally serves as the final transition to the customer and often provides a local grounding reference. Most distribution circuits have hundreds of distribution transformers. Distribution feeders may also have other transformers: voltage regulators, feeder step banks to interface circuits of different volt- ages, and grounding banks.
Basics
A transformer efficiently converts electric power from one voltage level to another. A transformer is two sets of coils coupled together through a mag- netic field. The magnetic field transfers all of the energy (except in an autotransformer). In an ideal transformer, the voltages on the input and the output are related by the turns ratio of the transformer:
where XL is the leakage reactance in ohms as seen from winding 1, and I1 is the current out of winding 1.
The current also transforms by the turns ratio, opposite of the voltage as
The “ampere-turns” stay constant at N1I1 = N2 I2 ; this fundamental relationship holds well for power and distribution transformers.
A transformer has a magnetic core that can carry large magnetic fields.
The cold-rolled, grain-oriented steels used in cores have permeabilities of over 1000 times that of air. The steel provides a very low-reluctance path for magnetic fields created by current through the windings.
Consider voltage applied to the primary side (source side, high-voltage side) with no load on the secondary side (load side, low-voltage side). The winding draws exciting current from the system that sets up a sinusoidal magnetic field in the core. The flux in turn creates a back emf in the coil that limits the current drawn into the transformer. A transformer with no load on the secondary draws very little current, just the exciting current, which is normally less than 0.5% of the transformer’s full-load current. On the unloaded secondary, the sinusoidal flux creates an open-circuit voltage equal to the primary-side voltage times the turns ratio.
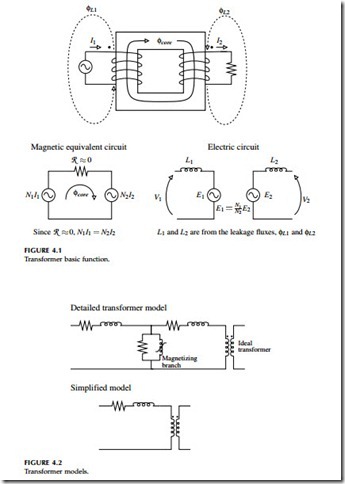
When we add load to the secondary of the transformer, the load pulls current through the secondary winding. The magnetic coupling of the secondary current pulls current through the primary winding, keeping constant ampere-turns. Normally in an inductive circuit, higher current creates more flux, but not in a transformer (except for the leakage flux). The increasing force from current in one winding is countered by the decreasing force from current through the other winding (see Figure 4.1). The flux in the core on a loaded transformer is the same as that on an unloaded transformer, even though the current is much higher.
The voltage on the primary winding determines the flux in the transformer (the flux is proportional to the time integral of voltage). The flux in the core determines the voltage on the output-side of the transformer (the voltage is proportional to the time derivative of the flux).
Figure 4.2 shows models with the significant impedances in a transformer.
The detailed model shows the series impedances, the resistances and the reactances. The series resistance is mainly the resistance of the wires in each winding. The series reactance is the leakage impedance. The shunt branch is the magnetizing branch, current that flows to magnetize the core. Most of the magnetizing current is reactive power, but it includes a real power component. Power is lost in the core through:
• Hysteresis — As the magnetic dipoles change direction, the core heats up from the friction of the molecules.
• Eddy currents — Eddy currents in the core material cause resistive losses. The core flux induces the eddy currents tending to oppose the change in flux density.
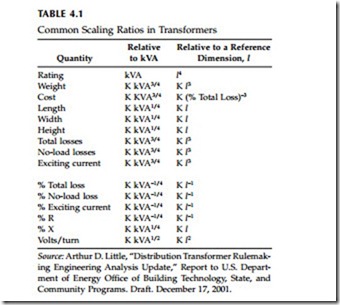
The magnetizing branch impedance is normally above 5,000% on a trans- former’s base, so we can neglect it in many cases. The core losses are often referred to as iron losses or no-load losses. The load losses are frequently called the wire losses or copper losses. The various parameters of transformers scale with size differently as summarized in Table 4.1.
The simplified transformer model in Figure 4.2 with series resistance and reactance is sufficient for most calculations including load flows, short-circuit calculations, motor starting, or unbalance. Small distribution transformers have low leakage reactances, some less than 1% on the transformer rating, and X/R ratios of 0.5 to 5. Larger power transformers used in distribution substations have higher impedances, usually on the order of 7 to 10% with X/R ratios between 10 and 40.
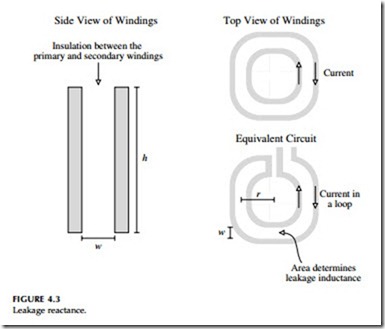
The leakage reactance causes voltage drop on a loaded transformer. The voltage is from flux that doesn’t couple from the primary to the secondary winding. Blume et al. (1951) describes leakage reactance well. In a real transformer, the windings are wound around a core; the high- and low- voltage windings are adjacent to each other. Figure 4.3 shows a configuration; each winding contains a number of turns of wire. The sum of the current in each wire of the high-voltage winding equals the sum of the currents in the Side View of Windings
low-voltage winding (N1I1 = N2I2), so each winding is equivalent to a busbar. Each busbar carries equal current, but in opposite directions. The opposing currents create flux in the gap between the windings (this is called leakage flux). Now, looking at the two windings from the top, we see that the wind- ings are equivalent to current flowing in a loop encompassing a given area. This area determines the leakage inductance.
The leakage reactance in percent is based on the coil parameters and separations (Blume et al., 1951) as follows:
In general, leakage impedance increases with:
• Higher primary voltage (thicker insulation between windings)
• kVA rating
• Larger core (larger diameter leads to more area enclosed)
Leakage impedances are under control of the designer, and companies will make transformers for utilities with customized impedances. Large distribution substation transformers often need high leakage impedance to control fault currents, some as high as 30% on the base rating.
Mineral oil fills most distribution and substation transformers. The oil provides two critical functions: conducting heat and insulation. Because the oil is a good heat conductor, an oil-filled transformer has more load-carrying capability than a dry-type transformer. Since it provides good electrical insulation, clearances in an oil-filled transformer are smaller than a dry-type transformer. The oil conducts heat away from the coils into the larger thermal mass of the surrounding oil and to the transformer tank to be dissipated into the surrounding environment. Oil can operate continuously at high temperatures, with a normal operating temperature of 105°C. It is flammable; the flash point is 150°C, and the fire point is 180°C. Oil has high dielectric strength, 220 kV/in. (86.6 kV/cm), and evens out voltage stresses since the dielectric constant of oil is about 2.2, which is close to that of the insulation. The oil also coats and protects the coils and cores and other metal surfaces from corrosion.