General Characteristics of Aggregate Wind Power
Aggregate wind power is defined as the sum of the real power delivered by all wind plants in a system as measured at their point of interconnection with the grid. We are concerned with both the instantaneous and moment-to-moment variations of aggregate wind power. The statistical characteristics of instantaneous aggregate wind power provide information about the uncertainty, whereas the statistical characteristics of moment-to-moment variation of aggregate wind power provide information about the variability. Rather than formulating models in the power domain, it is more useful to do so in the normalized power domain. This facilitates easier comparison and allows the models to be scaled to the desired capacity level, increasing their applicability. The units in the normalized power domain are per- unit (p.u.), where the normalization is done with respect to the total capacity of the wind plants in the system.
The characteristics of aggregate wind power are derived from—but different than—the characteristics of wind power from individual wind plants. Aggregate wind power is strongly influenced by the geographic diversity of the wind plants in the system. Geographic diversity is a term describing the tendency for wind plants in different wind regimes and separated by large distances to exhibit low correlation in their instantaneous wind power and moment-to-moment variations.
Many aspects of geographic diversity have been widely explored in the literature [7–21]. All other things being equal, a system with high geographic diversity has lower variability and uncertainty than one with low geographic diversity. The reduction of variability caused by geographic diversity is also known as the smoothing effect. The benefits of high geographic diversity include less frequent occurrences of extremely high and low power output; less frequent ramp events; and improved accuracy of wind power forecasts. The results are greater economy and reliability, decreased reserve requirements, and more efficient commitment and dispatch of generators [22].
Uncertainty of Aggregate Wind Power
We first consider the uncertainty characteristics of aggregate wind power. The definition of uncertainty can be subjective, with several appropriate interpretations possible, depending on the application or situation. For example, a system operator may be concerned about the probability of extremely high or low aggregate wind power. In this case uncertainty is best measured using quantiles. Another operator may be interested in the general spread of potential values of aggregate wind power, in which case the standard deviation is an appropriate measure. Rather than strictly defining uncertainty, our approach is to recognize that the uncertainty information of aggregate wind power is contained in its probability density function, from which the quantiles, standard deviation, and other metrics of uncertainty can be measured or computed.
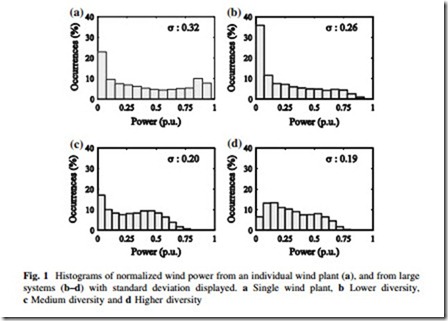
The shape of the probability density function can be approximated by constructing an empirical histogram of instantaneous aggregate wind power. Figure 1a shows a typical histogram of wind power from an individual wind plant and is provided for comparison purposes. Figure 1b–d shows aggregate wind power from three large systems. We will discuss the specific details of these systems and others in greater detail in Sect. 6. For now it suffices to know that each system has over 4 GW of installed wind capacity—a considerable amount. The computed standard deviation is provided with each plot. From inspection of Fig. 1, we make two important observations: (1) the modality of the wind power from an individual wind plant is different from that of wind power aggregated across a large system, and (2) different systems exhibit different uncertainty characteristics.
By most measures, the system corresponding to Fig. 1b has higher uncertainty than other systems. The standard deviation is greater than in other systems, and there are more frequent occurrences of zero and near rated (1.0 p.u.) power
production. These characteristics are similar to those of the individual wind plant, and as such the system can be described as having low geographic diversity. The wind plants in systems with low geographic diversity are often in close proxim- ity—perhaps separated by 200 km or less—and are in the same or similar wind regime. The Bonneville Power Administration (BPA) is an example of a system with low geographic diversity.
The system corresponding to Fig. 1c exhibits less uncertainty than Fig. 1b. The standard deviation and occurrences of low output are reduced, and the maximum power output rarely exceeds 0.75 p.u. Figure 1d exhibits the lowest uncertainty of the systems, which is characteristic of a system with appreciable geographic diversity. Episodes of extremely low and high production are rare, and the standard deviation is lower than the others. Systems with this level of geographic diversity tend to have wind plants spread over very large territories. The Midwest ISO (MISO) and PJM systems are examples of systems with higher geographic diversity.
It is evident that there is no proto-typical histogram or probability density function of instantaneous aggregate wind power, and so the uncertainty will vary depending on system specifics—mainly the level of geographic diversity. Our approach, therefore, is to seek a flexible multi-parametric model capable of rep- resenting the commonly exhibited probability density function shapes by systems with various levels of geographic diversity.
Variability of Aggregate Wind Power
Instantaneous wind power values provide us with information on uncertainty, but we are also interested in wind power variability. The variability of wind power is examined through the statistical characteristics of wind power variation. Wind power variation is defined as the difference in instantaneous wind power at two points in time, usually 1 h: DP½t] ¼ P½t] – P½t – q] where DP is the variation of wind power, t is the time, and q is the variation period. Similar to our approach with uncertainty, the variability of aggregate wind power is assessed by considering the probability density function of DP, as well as its statistical characteristics such as standard deviation and quantiles. We will see that variability in aggregate wind power is strongly influenced by geographic diversity.
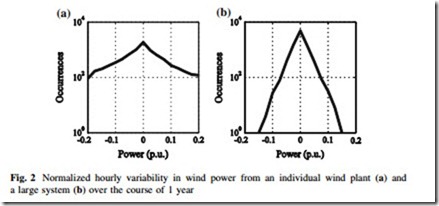
Figure 2 shows typical normalized hour-to-hour wind power variation in an individual wind plant (a) and system (b) over a period of 1 year. Note that for clarity the ordinate is logarithmically scaled. The trace for the individual wind plant is much broader than for the system aggregate, indicating more frequent extreme variability. Aggregation, therefore, tends to smooth wind power variability. In Fig. 2a, b, the nearly linear decrease in occurrences on the logarithmically scaled ordinate suggests that an appropriate parametric model will have an exponential form. The slope of the decrease is influenced by the geographic diversity of the system, as well as the variation period, with shorter periods having steeper slopes.
In the above we have briefly described typical uncertainty and variability characteristics of aggregate wind power. These characteristics depend on the geographic diversity in a system, as well as the characteristics of the constituent individual wind plants. Therefore in order to thoughtfully propose aggregate wind power models, we must begin by modeling individual wind plants and then establishing the mathematical framework for geographic diversity’s effect on uncertainty and variability.