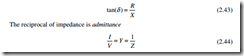Circuits
DC circuits
DC may be supplied by a battery or fuel cell, dc generator or a rectified power supply. The power flowing in a dc circuit is the product of the voltage and current
Power in a resistor is converted directly into heat.
When two or more resistors are connected in series, they carry the same current but their voltages must be added together (Fig. 2.7)
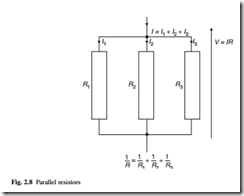
When two or more resistors are connected in parallel, they have the same voltage but their currents must be added together (Fig. 2.8)
A complicated circuit is made of several components of branches connected together at nodes forming one or more complete circuits, loops or meshes. At each node, Kirchhoff ’s current law (Fig. 2.9(a)) says that the total current flowing into the node must be balanced by the total current flowing out of the node. In each loop, the sum of all the voltages taken in order around the loop must add to zero, by Kirchhoff’s voltage law (Fig. 2.9(b)). Neither voltage nor current can be lost in a circuit.
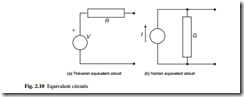
DC circuits are made of resistors and voltage or current sources. A circuit with only two connections to the outside world may be internally complicated. However, to the outside world it will behave as if it contains some resistance and possibly a source of voltage or current. The Thévenin equivalent circuit consists of a voltage source and a resistor (Fig. 2.10 (a)), while the Norton equivalent circuit consists of a current source and a resistor (Fig. 2.10(b)). The resistor equals the internal resistance of the circuit, the The´venin voltage source equals the open-circuit voltage, and the Norton current source is equal to the short-circuit current.
Many circuits contain more than one source of voltage or current. The current flowing in each branch, or the voltage at each node, can be found by considering each source separately and adding the results. During this calculation by superposition, all sources except the one being studied must be disabled: voltage sources are short- circuited and current sources are open-circuited. In Fig. 2.11, each of the loop currents I1 and I2 can be found by considering each voltage source separately and adding the results, so that I1 = I1a + I1b and I2 = I2a + I2b.
AC circuits
AC is supplied through a power system from large ac generators or alternators, by a local alternator, or by an electronic synthesis. AC supplies are normally sinusoidal, so that at any instant the voltage is given by
Vmax is the peak voltage or amplitude, w is the angular frequency (rad s-1) and f the phase angle (rad). The angular frequency is related to the ordinary frequency f (Hz) by
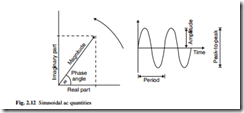
and the period is 1/f. The peak-to-peak or pk–pk voltage is 2Vmax, and the root mean square or rms voltage is Vmax / 2 . It is conventional for the symbols V and I in ac circuits to refer to the rms values, unless indicated otherwise. AC voltages and currents are shown diagrammatically on a phasor diagram (Fig. 2.12).
It is convenient to represent ac voltages using complex numbers. A sinusoidal voltage can be written
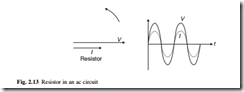
A resistor in an ac circuit behaves the same as in a dc circuit, with the current and volt- age in phase and related by the resistance or conductance (Fig. 2.13).
The current in an inductor lags the voltage across it by 90° (p/2 rad) (Fig. 2.14). The ac resistance or reactance X of an inductor increases with frequency
The direction of the phase shift in inductors and capacitors is easily remembered by the mnemonic CIVIL (i.e. C-IV, VI-L). Imperfect inductors and capacitors have some inherent resistance, and the phase lead or lag is less than 90°. The difference between the ideal phase angle and the actual angle is called the loss angle d. For a component of reactance X having a series resistance R
Combinations of resistors, capacitors and inductors will have a variation of impedance or admittance with frequency which can be used to select signals at certain frequencies in preference to others. The circuit acts as a filter, which can be low-pass, high-pass, band-pass, or band-stop.
An important filter is the resonant circuit. A series combination of inductor and capacitor has zero impedance (infinite admittance) at its resonant frequency
A parallel combination of inductor and capacitor has infinite impedance (zero admittance) at the same frequency.
In practice a circuit will have some resistance (Fig. 2.16), which makes the resonant circuit imperfect. The quality factor Q of a series resonant circuit with series resistance R is given by