Abstract The optimal energy management in energy hubs has recently attracted a great deal of attention around the world. The energy hub consists of several inputs (energy resources) and outputs (energy consumptions) and also some energy conversion/storage devices. The energy hub can be a home, large consumer, power plant, etc. The objective is to minimize the energy procurement costs (fuel/electricity/environmental aspects) subject to a set of technical constraints. One of the popular options to be served as the input resource is renewable energy like wind or solar power. Using the renewable energy has various benefits such as low marginal costs and zero environmental pollution. On the other hand, the uncertainties associated with them make the operation of the energy hub a difficult and risky task. Besides, there are other resources of uncertainties such as the hourly elec- tricity prices and demand values. Hence, it is important to determine an economic schedule for energy hubs, with an acceptable level of energy procurement risk. Thus, in this chapter a comprehensive multiobjective model is proposed to min- imize both the energy procurement cost and risk level in energy hub. For con- trolling the pernicious effects of the uncertainties, conditional value at risk (CVaR) is used as risk management tool. The proposed model is formulated as a mixed integer nonlinear programming (MINLP) problem and solved using GAMS.
Introduction
Problem Statement
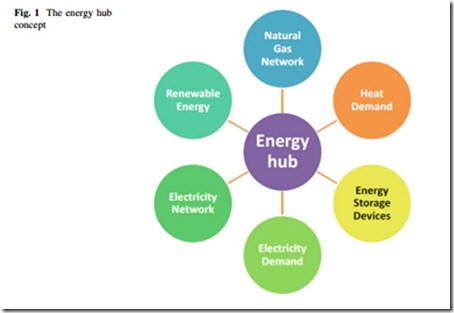
The increasing price of fuel and energy, combined with environmental laws and regulations, have led many different energy producers to integrate renewable, clean energy sources with nonrenewable ones, forming the idea of energy hubs. A typical energy hub consists of energy transformation devices, some distributed energy generation potential, electrical load, heat load, and some energy storage capabilities. The energy hub can be a commercial building, large consumer, power plant, etc. Figure 1 shows an example energy hub, which provides interface between participants, i.e., the energy producers, consumers, and storage along with the transportation infrastructure.
In this chapter, a risk averse stochastic framework is proposed for optimal energy management of an energy hub. The problem is analyzed with the following constraints, decision variables, and objective function:
• Decision variables:
– Electricity purchase from the electricity market.
– Gas purchase from the gas network.
– Operation schedule of energy storage/conversion devices.
• Constraints:
– Uncertainty of electricity prices.
– Uncertainty of electricity demand.
– Uncertainty of energy production of renewable resources.
– Technical constraints of energy conversion/storage devices.
– Demand balance.
– Risk of energy procurement from different resources.
Review of Related Works
A comprehensive framework for modeling of energy systems composed of multiple energy carriers has been presented in [1]. Different energy careers such as electricity, heat, gas, and biomass are considered. The modeling framework is
based on the energy hub approach. They have used conversion matrix for modeling the interactions between different participants of the energy hub. The modeling is deterministic and the effects of the uncertainties are not considered. A model based on energy hub concept, for the analysis of reliability of supply in multicarrier energy systems has been presented in [2]. It is concluded that con- sidering the mutual interconnections between multiple energy careers increases the supply redundancy and reliability. In [3] an optimization method is proposed for determination of optimal size of hybrid power systems, based on the energy hub concept.
In [4] and [5] an energy hub Monte Carlo valuation model is proposed. By means of this model, integrated systems of multienergy conversion and storage devices can be valued together with load management schemes. The energy hub’s ability to flexibly adapt its output to uncertain and volatile market prices is explicitly considered. In [6] the energy hub framework is adopted to determine a modeling procedure for a generic building energy system. In [7] application of model predictive control (MPC) to multicarrier energy systems including storage devices, renewable infeeds, and forecast uncertainties is studied. Due to the forecast errors in price and load profiles, the MPC strategy is used for reduction of the consequences of forecast uncertainties. Reference [8] proposes a tool for analyzing large-scale interconnected energy hub networks. Electrical and natural gas networks, wind generating capacity, district heat loads, converters, and energy storage are considered as the main elements of energy. In [9] a generic framework is proposed that allows the analysis of energy efficiency in multicarrier energy systems taking into account the physical properties of the energy networks. It is shown that a trade-off should be made between the cost minimization and maximization of energy efficiency in these systems.
Different methods have been used to model wind uncertainty. Scenario-based stochastic optimization modeling has been proposed in [10–12]. In this method some scenarios are generated as the representatives of the wind generation based on the a presumed probability distribution function. Although different risk mea- sures can be used to model risk, CVaR is used widely as a risk measure in scenario-based methods. CVaR has been used in [10, 11] for risk modeling of wind power generation uncertainty. Fuzzy scenario-based has been used in [13] for modeling wind uncertainty. The Interval optimization is also used in [14] in for uncertainty handling of wind power. This method is compared with scenario-based methods in [15].