Results
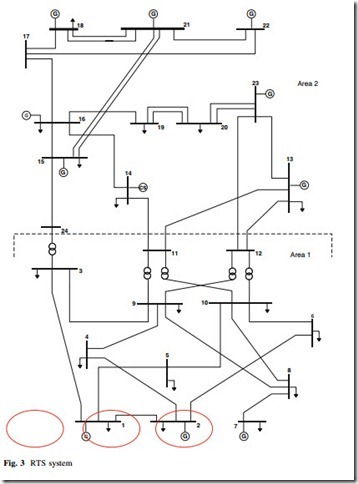
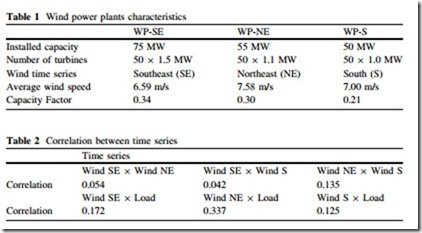
To evaluate the model presented in this chapter, a modified version of the IEEE reliability test system (RTS) [15], shown in Fig. 3, is used. The original genera- tion, composed of thermal, hydro, and nuclear units with installed capacity of 3,405 MW, is enlarged by the addition of three wind power plants, whose details are summarized in Table 1. The wind power plant WP-SE was added to busbar 1, WP-NE was added to busbar 2 and WP-S was added to busbar 7 of Fig. 3.
The characteristics of the wind time series Southeast (SE), Northeast (NE), and South (S) are described in [11]. The forced outage rate (FOR) and mean time to repair of the wind (MMTR) turbine/generator group are equal to 4 % and 97 h, respectively. The system load is represented by the time series described in [15]. The original load curve has been increased by 10 % leading to an average annual load of 1,862 MW.
The correlations between the wind time series and the load are shown in Table 2.
It can be seen that the wind series are not independent, although the correlation between them is small. However, the correlation between the wind series and the load is more significant, especially with the NE wind. As will be shown in the results, correlations of this magnitude are enough to produce completely incorrect evaluations if the independent approach is adopted. The higher the correlation the more incorrect are the results, except for the case when the time series are fully correlated, in which case they may be treated as one.
The simulations have been performed using the computational model RelSim developed in [16]. It was adopted a maximum coefficient of variation (a) of 3 % for all reliability indices. For all studies, the indices LOLP, EPNS, and LOLF were obtained by sequential MCS, considered as reference, and by nonsequential MCS using the independent and the proposed approaches, for sake of comparison.
Case 1: Variable Load and No Wind Farm
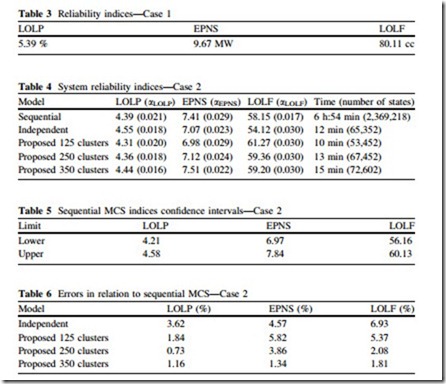
As a reference to evaluate the impact of the connection of wind power plants to the system, the reliability indices considering the time-varying load and no wind
First of all, it can be noticed the improvement of the system reliability by the addition of wind generation. Taking the sequential simulation results for comparison with the previous case, the connection of the two wind farms reduced the LOLP of 1 %, the EPNS of 2.26 MW, and the LOLF of 21.96 occurrences. However, due to the intermittent nature of wind generation, as well as transmission constraints, the reliability benefit is not as large as the generation capacity added to the system (130 MW or 3.67 %).
In order to evaluate the precision of the models, the confidence intervals for the indices obtained by sequential MCS with 95 % confidence are shown in Table 5 and the errors between the indices obtained by the models in relation to the sequential MCS are shown in Table 6.
Regarding the independent approach, it can be noted that the indices obtained are not accurate, showing the inadequacy of such a model to represent correlated time-varying variables. This is evident by the fact that they are not within the confidence intervals of the indices calculated by sequential MCS and that the percentage errors are higher than the coefficient of variation adopted for all indices.
On the other hand, all the indices obtained by the proposed model for all numbers of clusters are within the respective confidence intervals. Regarding the percentage errors, the improvement in the accuracy of the proposed model with increasing number of clusters is clear, especially for the EPNS index, with all indices errors being less than the coefficient of variation with 350 groups.
The computational performance of the proposed model is much better than the sequential simulation (up to 41.4 times faster). It is important to emphasize that the computational cost for obtaining the proposed Markov model is already
incorporated in the computing time reported. The increase in the number of clusters does not burden the model efficiency significantly. For example, doubling the number of clusters (125–250) requires only 30 % additional processing time, while multiplying it by 2.8 (125–350) implies in only 50 % extra time.
Therefore, it can be concluded that the proposed model with 350 clusters is as accurate as the sequential simulation and requires a computational effort of the same order as the independent approach, which is completely inaccurate.
Case 3: Constrained Transmission Network
In order to extend the evaluation of the proposed model, another modification to the RTS system has been done, which consists in reducing by half the maximum capacity of transmission lines. The objective is to examine how a more constrained transmission network would impact on the accuracy and efficiency of the model.
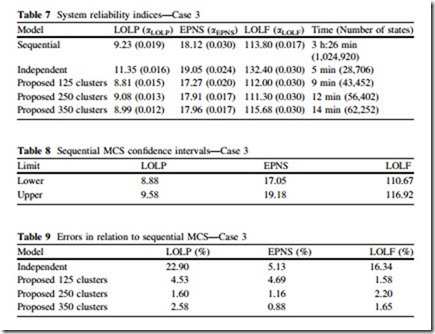
The results obtained for this case are shown in Table 7, the confidence intervals for the indices obtained by sequential MCS with 95 % confidence in Table 8 and
the errors between the indices obtained by the models in relation to the sequential MCS are shown Table 9.
Initially it is interesting to notice how this modification has impacted on the reliability of the system, with all the indices becoming more than twice the values of the previous case. This serves to highlight the importance of the transmission system in composite reliability evaluation.
The results of the independent model are even worse than those obtained for the previous case. The percentage errors are very high, especially for the LOLP and LOLF indices, showing again that this approach fails to estimate the indices correctly.
In general, the results of the proposed model showed the same good behavior observed previously, with all indices being within the interval of confidence of the indices calculated by sequential MCS. The only exception is the LOLP index for 125 clusters that was out of range for a small difference.
The percentage errors remained also low, confirming the validity of the pro- posed model for a transmission constrained network. An interesting observation is that the use of 250 clusters to represent the time series is enough in this case to obtain indices with errors smaller than the coefficient of variation. Although the indices with 350 clusters have been calculated, it would not be necessary to increase the number of groups beyond 250 clusters.
The good computational performance of the proposed model is also confirmed in this case. Considering 250 clusters, it was 17.17 times faster than the sequential simulation and obtains indices as accurate as it.
Case 4: Three Wind Farms and Variable Load
In order to evaluate the impact of a larger penetration level of wind generation on the system reliability and also to explore the performance of the model for a larger number of time-varying variables, the reliability indices were calculated considering the connection of the third wind farm WP-S to the system with the original transmission network and using the same time-varying load.
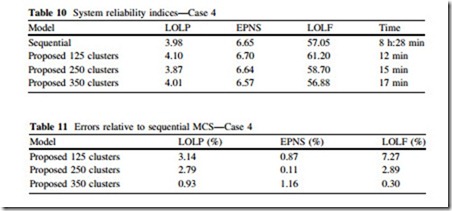
The results obtained for this case are shown in Table 10 and the errors between the indices obtained by the models in relation to the sequential MCS are shown in Table 11. The coefficients of variation off all indices are smaller than 3 %.
The accuracy of the proposed model is again confirmed for this case with three different wind farms and variable load. The percentage errors in relation to the sequential simulation are low for all indices, except for the LOLF index when using 125 clusters.
In terms of computational performance, the proposed model has demonstrated to be very efficient even with an increased number of time series. Considering the most time-consuming simulation (with 350 clusters), it was about 30 times faster than the sequential simulation. An interesting characteristic to be highlighted is the little extra computation time required by the proposed model due to the addition of another wind generation, what can be seen by comparing with the simulation time required by Case 2.
The addition of a new wind farm has slightly reduced the reliability indices in relation to Case 2, but not proportionally to the amount of added generation capacity. The addition of 50 MW of WP-S has increased the wind generation penetration level from 3.67 % (Case 2) to 5.02 % in terms of installed capacity and from 6.98 to 9.66 % in terms of load demand. However, the EPNS and LOLP indices have only reduced by 0.76 MW and 0.41 %, respectively. These effects are due to the intermittency of wind generation and consequently low capacity factor, and must be taken into consideration when planning a larger penetration of wind generation.