Simulation Results
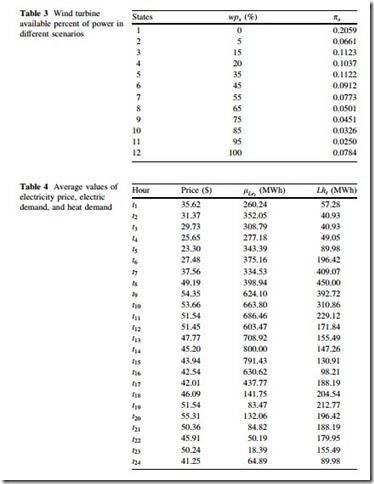
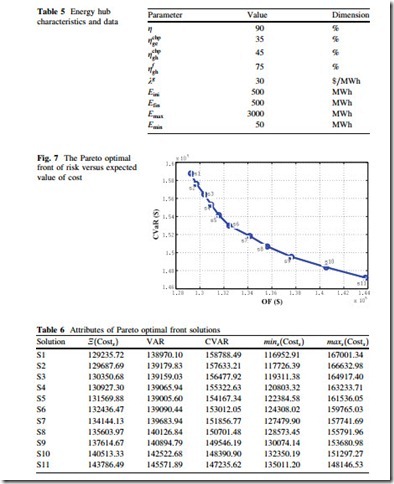
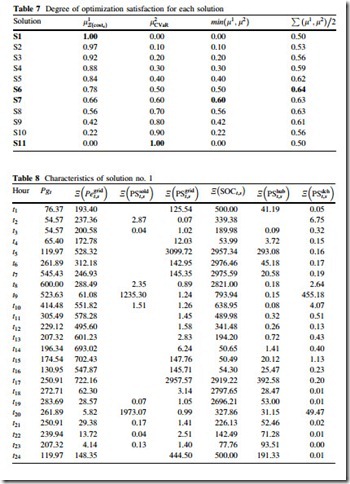
The proposed approach is implemented in GAMS [38] environment solved by DICOPT solver running on an Intel Core 2 Duo Processor T5300 (1.73 GHz) PC with 1 GB RAM. It is applied to a 5-thermal units system as described in Table 2. The cost coefficients of the thermal units are adapted from [39]. The UTi and DTi for all units are considered to be 5 and 2 h, respectively. The available percent of wind capacity in each wind speed scenario is given in Table 3. The total wind capacity (i.e., Pr ) is assumed to be 300 MW. The mean values of electricity prices, electricity demand, and heat demand for the upcoming day are given in Table 4. The corresponding standard deviations (r) is assumed to be 1 % of the mean values given in Table 4. The energy hub characteristics and data are described in Table 5.
Pareto Optimal Front Determination
The proposed risk-based energy management strategy is solved using multiob- jective optimization technique and the Pareto optimal front of the solutions is obtained as depicted in Fig. 7. The concept of Pareto optimality is explained in
Appendix-II. This front is obtained using e-constraint method, which is an efficient technique to solve problems with non-convex Pareto front. This method sets an upper limit for one objective function and minimizes the other one. This limit is gradually decreased and the Pareto front is obtained. The next step after finding the
Pareto optimal front is the selection of final solution which is done using fuzzy satisfying approach [20] (see Appendix-III). The attributes of Pareto optimal front solutions are described in Table 6.
Using the technique described in Appendix-III, the degree of optimization satis- faction is calculated for each solution as shown in Table 7.
In order to clarify the final solution selection, four different decision-making options are considered. Each option represents a unique attitude of decision-maker toward the risk and cost of energy hub management. Next, each option is described and analyzed.
Using the technique described in Appendix-III, the degree of optimization satisfaction is calculated for each solution as shown in Table 7.
In order to clarify the final solution selection, four different decision-making options are considered. Each option represents a unique attitude of decision-maker toward the risk and cost of energy hub management. Next, each option is described and analyzed.
(1) Risk neutral attitude
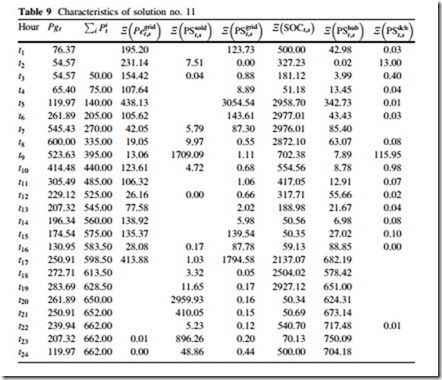
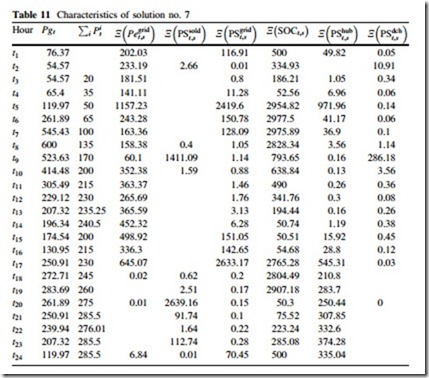
In this option, the decision-maker neglects the risk and tries to minimize the expected costs. The best solution for this purpose is solution no. 1. This solution has the maximum value of lNðcosts Þ compared to other solutions. The characteristics of this solution are given in Table 8.
The simulation results show that the thermal units are off for this option since it only uses the gas and electricity power pool to meet the different demands. It also
(2) Risk averse attitude
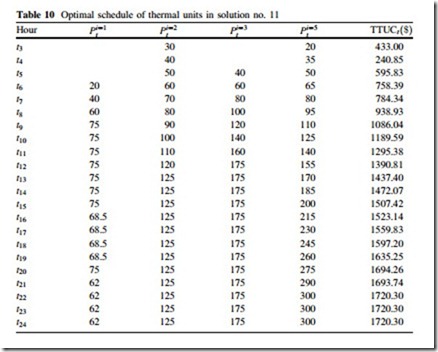
In some situations, the cost issue does not matter while risk issue constitutes the whole concerns. This option deals with such a situation where the most important issue for the decision maker is the risk and it tries to minimize CVaR. The best solution for this purpose is solution no. 11. This solution has the minimum value of lCVaR com- pared to other solutions. The characteristics of this solution are given in Table 9.
The optimal schedule of thermal units in solution no. 11 are given in Table 10.
(3) Conservative trade-off between risk and cost attitude
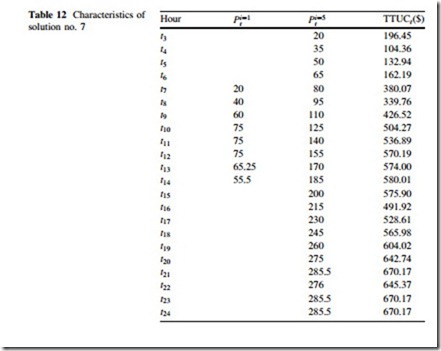
In some situations, both risk and cost are important and none of them should be degraded. This option deals with such a situation where the most attractive solution is the one which has the maximum value of minimum satisfaction of objective functions. The best solution in this option is solution no. 7. This solution has the In some situations, both risk and cost are important but it is accepted that if one of them is degraded to significantly improve the other one. This option deals with such a situation where the most attractive solution is the one which has the maximum value of sum of satisfaction of objective functions. The best solution in this regard is solution no. 6. This solution has the degree of satisfaction for lCVaR ¼ 0:5 and Nðcosts Þ ¼ 0:78. The characteristics of this solution are given in Table 13.
The optimal schedule of thermal units in solution no. 6 are given in Table 14.