UNBALANCED SUPPLY VOLTAGES

Steady state performance with unbalanced supply voltages may be treated by the method of symmetrical components. The three-wire supply voltages V_a, V_b, V_c are decomposed into forward and backward components:

V_af ^{= 1}3 (V_a + aV_b + a2V_c ); a = ej23π (7.115)

Vab = 13 (Va + a2Vb + aVc );

V_bf = a²V_af ; V_cf = aV_af ; V_bb = aV_ab; V_cb = a²V_ab; (7.116)

Note also that the slip for the forward component is S_f = S, while for the backward component, S_b is

S_b = −_−^pf₁¹pf^_11−n = 2−S (7.117)

_

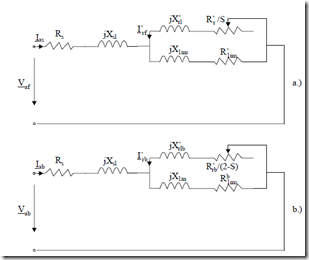
So, in fact, we obtain two equivalent circuits (Figure 7.26) as

V_a = V_af + V_ab (7.118)

I_a = I_af + I_ab (7.119)

Figure 7.26 Forward and backward component equivalent circuits per phase

For S = 0.01 – 0.05 and f₁ = 60(50) Hz, the rotor frequency for the backward components is f₂ = (2 – S)f₁ ≈ 100(120) Hz. Consequently, the rotor parameters R_r′ and L_rl′ are notably influenced by the skin effect, so

R_rb‘> R ‘; X_{r rlb}‘< X ‘_rl (7.120)

Also for the backward component, the core losses are notably less than those of, forward component. The torque expression contains two components:

3R ‘ I ‘r ( rf )² p1 + 3R ‘ I ‘rb ⁽ rb )² p

Te = _{S ω}1 (_2−S) (_−ω1 1) (7.121)

With phase voltages given as amplitudes and phase shifts, all steady-state performance may be calculated with the symmetrical component method. The voltage imbalance index V_imbalance (in %) may be defined as

Vimbalance = ∆VVavemax 100%; V∆ max = Vmax − Vmin; Vave = (Va + V3b + Vc ) (7.122)

V_max = maximum phase voltage; V_min = phase with minimum voltage.

An alternative definition would be

V_unb[ ]% ^{= V}_V^abaf 100

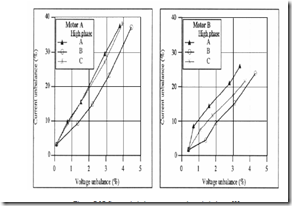
Figure 7.27 Current imbalance versus voltage imbalance [2]

a.) cost optimized motor (motor A)

b.) premium motor (motor B)

Due to very different values of slip and rotor parameters for forward and backward components, a small voltage imbalance is likely to produce a rather large current imbalance. This is illustrated in Figure 7.27.

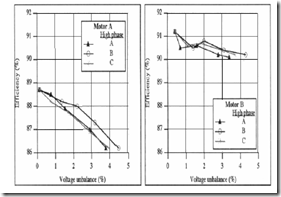
Also, for rated slip (power), the presence of backward (braking) torque and its losses leads to a lower efficiency η. ω1 (1−S)

Te

η = 3Re [V PI1 * + Vab Iab* ] (7.124)

af af

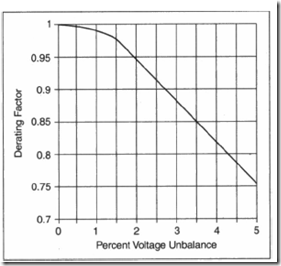
Apparently cost-optimised motors–with larger rotor skin effect in general– are more sensitive to voltage imbalances than premium motors (Figure 7.28). [2] As losses in the IM increase with voltage imbalance, machine derating is to be applied to maintain rated motor temperature. NEMA 14.35 standards recommend an IM derating with voltage imbalance as shown in Figure 7.29. [3] Voltage imbalance also produces, as expected, 2f₁ frequency vibration. As small voltage imbalance can easily occur in local power grids, care must be exercised in monitoring it and the motor currents and temperature.

An extreme case of voltage imbalance is one phase open.

Figure 7.28. Efficiency versus voltage imbalance

a.) cost optimised motor

Figure 7.29. Derating versus voltage imbalance (NEMA Figure 14.1)

ONE STATOR PHASE IS OPEN

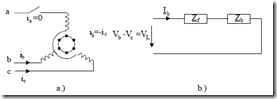
Let us consider the IM under steady state with one stator phase open (Figure 7.30a).

This time it is easy to calculate first the symmetrical current components I_af,

Iab, Iao.

I^af = 1 _I +

³1((I^aa +aaI2^bIb++aa2 II^cc ))₌= −a −a³−a32a_I2^bI=b = −jI^3bIaf (7.125)

Iab = 3i =-ic V -V =V_{b c L}

Figure 7.30 One stator phase is open

a.) phase a is open

b.) equivalent single phase circuit

Let us replace the equivalent circuits in Figure 7.26 by the forward and backward impedances Z_f, Z_b.

V_af = Z_f I_af ; V_ab = Z_{b ab}I (7.126)

Similar relations are valid for V_bf = a²V_af, V_bb = aV_ab , V_cf = aV_af, V_cb = a2Vab :

Vb −Vc = Vbf + Vbb −Vcf −(^V₂ cb_−a =)^a_Iaf^{2 Z}(_Zf ^I_f af₊+_Z^a_b )Zb abI −aZf Iaf −a² Zb abI = (7.127)

_{= a}

With (7.125),

V_b − V_c = I_b(Z_f + Z_b ) (7.128)

The electromagnetic torque still retains Equation (7.121), but (7.128) allows a handy computation of current in phase b and then from (7.115) through

(7.126), I_af and I_ab are calculated.

At standstill (S = 1) Z_f = Z_b = Z_sc (Figure 7.26) and thus the short-circuit current I_sc1 is

Isc1 = 2VZLsc = 23 VZphasesc = 23 Isc3 (7.129)

The short-circuit current I_sc1 with one phase open is thus 3 / 2 times smaller than for balanced supply. There is no danger from this point of view at start. However, as (Zf )S 1= = (Zb )S 1= , Irf′ = Irb′ and thus the forward and