Two-layer Winding
In this type of winding, there are two conductors or coil sides per slot arranged in two layers. Usually, one side of every coil lies in the upper half of one slot and other side lies in the lower half of some other slot at a distance of approximately one pitch away (Fig. 26.28). The transfer of the coil from one slot to another is usually made in a radial plane by means of a peculiar bend or twist at the back end as shown in Fig. 26.29. Such windings in which two coil sides occupy each slot are most commonly used for all medium-sized machines. Sometimes 4 or 6 or 8 coil sides are used in each slot in several layers because it is not practicable to have too many slots (Fig. 26.30). The coil sides lying at the upper half of the slots are numbered odd i.e. 1, 3, 5, 7 etc. while those at the lower half are numbered even i.e. 2, 4, 6, 8 etc.
Degree of Re-entrant of an Armature Winding
A winding is said to be single re-entrant if on tracing through it once, all armature conductors are included on returning to the starting point. It is double re-entrant if only half the conductors are included in tracing through the winding once and so on.
Multiplex Winding
In such windings, there are several sets of completely closed and independent windings. If there is only one set of closed winding, it is called simplex wave winding. If there are two such windings on the same armature, it is called duplex winding and so on. The multiplicity affects a number of parallel paths in the armature. For a given number of armature slots and coils, as the multiplicity increases, the number of parallel paths in the armature increases thereby increasing the current rating but decreasing the voltage rating.
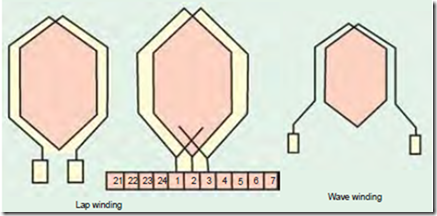
Lap and Wave Windings
Two types of windings mostly employed for drum-type armatures are known as Lap Winding and Wave Winding. The difference between the two is merely due to the different arrangement of the end connections at the front or commutator end of armature. Each winding can be arranged progressively or retrogressively and connected in simplex, duplex and triplex. The following rules, however, apply to both types of the windings :
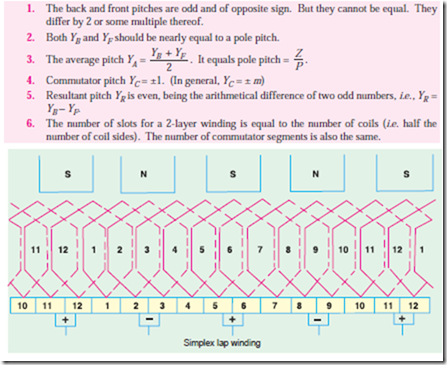
(i) The front pitch and back pitch are each approximately equal to the pole-pitch i.e. windings should be full-pitched. This results in increased e.m.f. round the coils. For special purposes, fractional-pitched windings are deliberately used (Art. 26.15).
(ii) Both pitches should be odd, otherwise it would be difficult to place the coils (which are former-wound) properly on the armature. For exmaple, if YB and YF were both even, the all the coil sides and conductors would lie either in the upper half of the slots or in the lower half. Hence, it would become impossible for one side of the coil to lie in the upper half. Hence, it would become impossible for one side of the coil to lie in the upper half of one slot and the other side of the same coil to lie in the lower half of some other slot.
(iii) The number of commutator segments is equal to the number of slots or coils (or half the number of conductors) because the front ends of conductors are joined to the segments in pairs.
(iv) The winding must close upon itself i.e. if we start from a given point and move from one coil to another, then all conductors should be traversed and we should reach the same point again without a break or discontinuity in between.
Simplex Lap-winding*
It is shown in Fig. 26.25 which employs single-turn coils. In lap winding, the finishing end of one coil is connected to a commutator segment and to the starting end of the adjacent coil situated under the same pole and so on, till and the coils have been connected. This type of winding derives its name from the fact it doubles or laps back with its succeeding coils.
Following points regarding simplex lap winding should be carefully noted :
Numbering of Coils and Commutator Segments
In the d.c. winding diagrams to follow, we will number the coils only (not individual turns). The upper side of the coil will be shown by a firm continuous line whereas the lower side will be shown by a broken line. The numbering of coil sides will be consecutive i.e. 1, 2, 3 ….. etc. and such that odd numbers are assigned to the top conductors and even numbers to the lower sides for a two-layer winding. The commutator segments will also be numbered consecutively, the number of the segments will be the same as that of the upper side connected to it.
The winding ends here because we come back to the conductor from where we started.
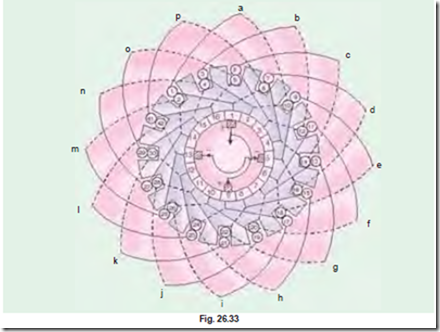
We will now discuss the developed diagram which is one that is obtained by imagining the armature surface to be removed and then laid out flat so that the slots and conductors can be viewed without the necessity of turning round the armature in order to trace out the armature windings. Such a developed diagram is shown in Fig. 26.31.
front we complete the winding, thus including every coil side once till we reach the coil side 1 from where we started. Incidentally, it should be noted that all upper coil sides have been given odd numbers, whereas lower ones have been given even numbers as shown in the polar diagram (Fig. 26.32) of the winding of Fig. 26.31.
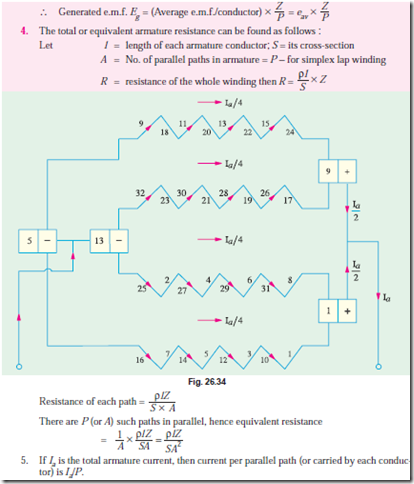
Brush positions can be located by finding the direction of currents flowing in the various conduc- tors. If currents in the conductors under the influence of a N-pole are assumed to flow downwards (as shown), then these will flow upwards in conductors under the influence of S-pole. By putting proper arrows on the conductors (shown separately in the equivalent ring diagram), it is found that commu- tator bars No. 1 and 9 are the meeting points of e.m.fs. and hence currents are flowing out of these conductors. The positive brushes should, therefore, be placed at these commutator bars. Similarly, commutator bars No. 5 and 13 are the separating points of e.m.fs. hence negative brushes are placed there. In all, there are four brushes, two positive and two negative. If brushes of the same polarity are connected together, then all the armature conductors are divided into four parallel paths.
Division of conductors into parallel paths is shown separately in the schematic diagram of Fig.
Obviously, if Ia is the total current supplied by the generator, then current carried by each parallel path is Ia/4.
Summarizing these conclusions, we have
1. The total number of brushes is equal to the number of poles.
2. There are as many parallel paths in the armature as the number of poles. That is why such a winding is sometimes known as ‘multiple circuit’ or ‘parallel’ winding. In general, number of parallel paths in armature = mP where m is the multiplicity (plex) of the lap winding. For example, a 6-pole duplex lap winding has (6 ´ 2) = 12 parallel paths in its armature.
3. The e.m.f. between the +ve and -ve brushes is equal to the e.m.f. generated in any one of the parallel paths. If Z is the total number of armature conductors and P the number of poles, then the number of armature conductors (connected in series) in any parallel path is Z/P.
Related posts:
Incoming search terms:
- multiplex winding
- double layer winding
- double layer winding diagram
- duplex wave winding
- two layer lap winding
- difference between simplex and multiplex winding
- Multiplex windings
- simplex winding
- duplex lap winding
- 36 slot 4 pole winding pdf
- double layer lap winding
- multyplex windinng of dc generator
- schematic diagram of a front pitch
- armature winding diagram
- 3 slot 2 pole bldc rewinding
- what is multiplex winding
- multiplex winding is used
- simplex lap winding diagram
- lap winding pic
- triplex winding diagram
- 24 slot moter winding 1 5hp
- triplex winding
- no of commutator bars for a 4 pole 2 layer dc lap winding with 24 slots and one conductor per layer is
- lap winding diagram
- three layer winding
- motor repair pdf
- two pole motor winding data
- two layer winding and multiplex winding
- line voltage of two layer lap winding
- duplex lap winding diagram
- simplex and duplex winding
- single layer winding and double layer winding
- triplex lap wound d c armature
- mush winding advantages
- 12 slot 24 commutator two sided winding
- 24 commutator 12 slot armature winding diagram
- 12coil 12segment 12slot 4pole of lap winding
- lap winding and wave winding pdf
- how many brushes for duplex double layer wave winding
- 24 slots armature paralle winding diagram
- duplex wave windings
- simplex and multiplex winding
- simplex double layer lap winding
- simplex lap and duplex lap wnding calculation
- duplex wave winding diagram
- pdf of angle grinder armature winding with commutator connection
- lap winding back pitch
- figure of multiturn multiplex armature winding
- Simplex and mu
- simplex and duplex lap winding