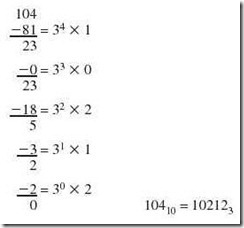The Essentials of Computer Organization and Architecture – Data Representation in Computer Systems

Data Representation in Computer Systems

2.1 Introduction

“What would life be without arithmetic, but a scene of horrors?”

—Sydney Smith (1835)

The organization of any computer depends considerably on how it represents numbers, characters, and control information. The converse is also true: Standards and conventions established over the years have determined certain aspects of computer organization. This chapter describes the various ways in which computers can store and manipulate numbers and characters. The ideas presented in the following sections form the basis for understanding the organization and function of all types of digital systems.

The most basic unit of information in a digital computer is called a bit, which is a contraction of binary digit. In the concrete sense, a bit is nothing more than a state of “on” or “off” (or “high” and “low”) within a computer circuit. In 1964, the designers of the IBM System/360 mainframe computer established a convention of using groups of 8 bits as the basic unit of addressable computer storage. They called this collection of 8 bits a byte.

Computer words consist of two or more adjacent bytes that are sometimes addressed and almost always are manipulated collectively. The word size represents the data size that is handled most efficiently by a particular architecture. Words can be 16 bits, 32 bits, 64 bits, or any other size that makes sense within the context of a computer’s organization (including sizes that are not multiples of eight). Eight-bit bytes can be divided into two 4-bit halves called nibbles (or nybbles). Because each bit of a byte has a value within a positional numbering system, the nibble containing the least-valued binary digit is called the low-order nibble, and the other half the high-order nibble.

2.2 Positional Numbering Systems

At some point during the middle of the sixteenth century, Europe embraced the decimal (or base 10) numbering system that the Arabs and Hindus had been using for nearly a millennium. Today, we take for granted that the number 243 means two hundreds, plus four tens, plus three units. Notwithstanding the fact that zero means “nothing,” virtually everyone knows that there is a substantial difference between having 1 of something and having 10 of something.

The general idea behind positional numbering systems is that a numeric value is represented through increasing powers of a radix (or base). This is often referred to as a weighted numbering system because each position is weighted by a power of the radix.

The set of valid numerals for a positional numbering system is equal in size to the radix of that system. For example, there are 10 digits in the decimal system, 0 through 9, and 3 digits for the ternary (base 3) system, 0, 1, and 2. The largest valid number in a radix system is one smaller than the radix, so 8 is not a valid numeral in any radix system smaller than 9. To distinguish among numbers in different radices, we use the radix as a subscript, such as in 33₁₀to represent the decimal number 33. (In this book, numbers written without a subscript should be assumed to be decimal.) Any decimal integer can be expressed exactly in any other integral base system (see Example 2.1).

Example 2.1:

Three numbers represented as powers of a radix.

243.51₁₀ = 2 x 10² + 4 x 10¹ + 3 x 10⁰ + 5 x 10^-1 + 1 x 10^-2

212₃ = 2 x 3² + 1 x 3¹ + 2 x 3⁰ = 23₁₀

10110₂ = 1 x 2⁴ + 0 x 2³ + 1 x 2² + 1 x 2¹ + 0 x 2⁰ = 22₁₀

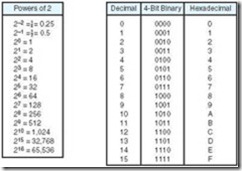
The two most important radices in computer science are binary (base two), and hexadecimal (base 16). Another radix of interest is octal (base 8). The binary system uses only the digits 0 and 1; the octal system, 0 through 7. The hexadecimal system allows the digits 0 through 9 with A, B, C, D, E, and F being used to represent the numbers 10 through 15. Figure 2.1 shows some of the radices.

2.3 Decimal To Binary Conversions

Gottfried Leibniz (1646–1716) was the first to generalize the idea of the (positional) decimal system to other bases. Being a deeply spiritual person, Leibniz attributed divine qualities to the binary system. He correlated the fact that any integer could be represented by a series of ones and zeros with the idea that God (1) created the universe out of nothing (0). Until the first binary digital computers were built in the late 1940s, this system remained nothing more than a mathematical curiosity. Today, it lies at the heart of virtually every electronic device that relies on digital controls.

Because of its simplicity, the binary numbering system translates easily into electronic circuitry. It is also easy for humans to understand. Experienced computer professionals can recognize smaller binary numbers (such as those shown in Figure 2.1) at a glance. Converting larger values and fractions, however, usually requires a calculator or pencil and paper. Fortunately, the conversion techniques are easy to master with a little practice. We show a few of the simpler techniques in the sections that follow.

2.3.1 Converting Unsigned Whole Numbers

We begin with the base conversion of unsigned numbers. Conversion of signed numbers (numbers that can be positive or negative) is more complex, and it is important that you first understand the basic technique for conversion before continuing with signed numbers.

Conversion between base systems can be done by using either repeated subtraction or a division-remainder method. The subtraction method is cumbersome and requires a familiarity with the powers of the radix being used. Being the more intuitive of the two methods, however, we will explain it first.

As an example, let’s say that we want to convert 104₁₀ to base 3. We know that 3⁴ = 81 is the highest power of 3 that is less than 104, so our base 3 number will be 5 digits wide (one for each power of the radix: 0 through 4). We make note that 81 goes once into 104 and subtract, leaving a difference of 23. We know that the next power of 3, 3³ = 27, is too large to subtract, so we note the zero “placeholder” and look for how many times 3² = 9 divides 23. We see that it goes twice and subtract 18. We are left with 5 from which we subtract 3¹ = 3, leaving 2, which is 2 x 3⁰. These steps are shown in Example 2.2.

Example 2.2:

Convert 104₁₀ to base 3 using subtraction.

The division-remainder method is faster and easier than the repeated subtraction method. It employs the idea that successive divisions by the base are in fact successive subtractions by powers of the base. The remainders that we get when we sequentially divide by the base end up being the digits of the result, which are read from bottom to top. This method is illustrated in Example 2.3.

Example 2.3:

Convert 104₁₀ to base 3 using the division-remainder method.

Reading the remainders from bottom to top, we have: 104₁₀ = 10212₃.

This method works with any base, and because of the simplicity of the calculations, it is particularly useful in converting from decimal to binary. Example 2.4 shows such a conversion.

Example 2.4:

Convert 147₁₀ to binary.

Reading the remainders from bottom to top, we have: 147₁₀ = 10010011₂.

A binary number with N bits can represent unsigned integers from 0 to 2^N-1. For example, 4 bits can represent the decimal values 0 through 15, while 8 bits can represent the values 0 through 255. The range of values that can be represented by a given number of bits is extremely important when doing arithmetic operations on binary numbers. Consider a situation in which binary numbers are 4 bits in length, and we wish to add 1111₂ (15₁₀) to 1111₂. We know that 15 plus 15 is 30, but 30 cannot be represented using only 4 bits. This is an example of a condition known as overflow, which occurs in unsigned binary representation when the result of an arithmetic operation is outside the range of allowable precision for the given number of bits. We address overflow in more detail when discussing signed numbers in Section 2.4.

2.3.2 Converting Fractions

Fractions in any base system can be approximated in any other base system using negative powers of a radix. Radix points separate the integer part of a number from its fractional part. In the decimal system, the radix point is called a decimal point. Binary fractions have a binary point.

Fractions that contain repeating strings of digits to the right of the radix point in one base may not necessarily have a repeating sequence of digits in another base. For instance, ²/₃ is a repeating decimal fraction, but in the ternary system it terminates as 0.2₃ (2 x 3^-1 = 2 x ¹/₃). We can convert fractions between different bases using methods analogous to the repeated subtraction and division-remainder methods for converting integers. Example 2.5 shows how we can use repeated subtraction to convert a number from decimal to base 5.

Example 2.5:

Convert 0.4304₁₀ to base 5.

Reading from top to bottom, we find 0.4304₁₀ = 0.2034₅.

Because the remainder method works with positive powers of the radix for conversion of integers, it stands to reason that we would use multiplication to convert fractions, because they are expressed in negative powers of the radix. However, instead of looking for remainders, as we did above, we use only the integer part of the product after multiplication by the radix. The answer is read from top to bottom instead of bottom to top. Example 2.6 illustrates the process.

Example 2.6:

Convert 0.4304₁₀ to base 5.

Reading from top to bottom, we have 0.4304₁₀ = 0.2034₅.

This example was contrived so that the process would stop after a few steps. Often things don’t work out quite so evenly, and we end up with repeating fractions. Most computer systems implement specialized rounding algorithms to provide a predictable degree of accuracy. For the sake of clarity, however, we will simply discard (or truncate) our answer when the desired accuracy has been achieved, as shown in Example 2.7.

Example 2.7:

Convert 0.34375₁₀ to binary with 4 bits to the right of the binary point.

Reading from top to bottom, 0.34375₁₀ = 0.0101₂ to four binary places.

The methods just described can be used to directly convert any number in any base to any other base, say from base 4 to base 3 (as in Example 2.8). However, in most cases, it is faster and more accurate to first convert to base 10 and then to the desired base. One exception to this rule is when you are working between bases that are powers of two, as you’ll see in the next section.

Example 2.8:

Convert 3121₄ to base 3.

2.3.3 Converting between Power-of-Two Radices

Binary numbers are often expressed in hexadecimal—and sometimes octal—to improve their readability. Because 16 = 2⁴, a group of 4 bits (called a hextet) is easily recognized as a hexadecimal digit. Similarly, with 8 = 2³, a group of 3 bits (called an octet) is expressible as one octal digit. Using these relationships, we can therefore convert a number from binary to octal or hexadecimal by doing little more than looking at it.

Example 2.9:

Convert 110010011101₂ to octal and hexadecimal.

If there are too few bits, leading zeros can be added.

2.4 Signed Integer Representation

We have seen how to convert an unsigned integer from one base to another. Signed numbers require additional issues to be addressed. When an integer variable is declared in a program, many programming languages automatically allocate a storage area that includes a sign as the first bit of the storage location. By convention, a “1” in the high-order bit indicates a negative number. The storage location can be as small as an 8-bit byte or as large as several words, depending on the programming language and the computer system. The remaining bits (after the sign bit) are used to represent the number itself.

How this number is represented depends on the method used. There are three commonly used approaches. The most intuitive method, signed magnitude, uses the remaining bits to represent the magnitude of the number. This method and the other two approaches, which both use the concept of complements, are introduced in the following sections.

2.4.1 Signed Magnitude

Up to this point, we have ignored the possibility of binary representations for negative numbers. The set of positive and negative integers is referred to as the set of signed integers. The problem with representing signed integers as binary values is the sign—how should we encode the actual sign of the number? Signedmagnitude representation is one method of solving this problem. As its name implies, a signed-magnitude number has a sign as its left-most bit (also referred to as the high-order bit or the most significant bit) while the remaining bits represent the magnitude (or absolute value) of the numeric value. For example, in an 8-bit word, –1 would be represented as 10000001, and +1 as 00000001. In a computer system that uses signed-magnitude representation and 8 bits to store integers, 7 bits can be used for the actual representation of the magnitude of the number. This means that the largest integer an 8-bit word can represent is 2⁷ – 1 or 127 (a zero in the high-order bit, followed by 7 ones). The smallest integer is 8 ones, or –127. Therefore, N bits can represent –2^{(N – 1)} – 1 to 2^{(N – 1)} –1.

Computers must be able to perform arithmetic calculations on integers that are represented using this notation. Signed-magnitude arithmetic is carried out using essentially the same methods as humans use with pencil and paper, but it can get confusing very quickly. As an example, consider the rules for addition: (1) If the signs are the same, add the magnitudes and use that same sign for the result; (2) If the signs differ, you must determine which operand has the larger magnitude. The sign of the result is the same as the sign of the operand with the larger magnitude, and the magnitude must be obtained by subtracting (not adding) the smaller one from the larger one. If you consider these rules carefully, this is the method you use for signed arithmetic by hand.

We arrange the operands in a certain way based on their signs, perform the calculation without regard to the signs, and then supply the sign as appropriate when the calculation is complete. When modeling this idea in an 8-bit word, we must be careful to include only 7 bits in the magnitude of the answer, discarding any carries that take place over the high-order bit.

Example 2.10:

Add 01001111₂ to 00100011₂ using signed-magnitude arithmetic.

The arithmetic proceeds just as in decimal addition, including the carries, until we get to the seventh bit from the right. If there is a carry here, we say that we have an overflow condition and the carry is discarded, resulting in an incorrect sum. There is no overflow in this example.

We find 01001111₂ + 00100011₂ = 01110010₂ in signed-magnitude representation.

Sign bits are segregated because they are relevant only after the addition is complete. In this case, we have the sum of two positive numbers, which is positive. Overflow (and thus an erroneous result) in signed numbers occurs when the sign of the result is incorrect.

In signed magnitude, the sign bit is used only for the sign, so we can’t “carry into” it. If there is a carry emitting from the seventh bit, our result will be truncated as the seventh bit overflows, giving an incorrect sum. (Example 2.11 illustrates this overflow condition.) Prudent programmers avoid “million dollar” mistakes by checking for overflow conditions whenever there is the slightest possibility that they could occur. If we did not discard the overflow bit, it would carry into the sign, causing the more outrageous result of the sum of two positive numbers being negative. (Imagine what would happen if the next step in a program were to take the square root or log of that result!)

Example 2.11:

Add 01001111₂ to 01100011₂ using signed-magnitude arithmetic.

We obtain the erroneous result of 79 + 99 = 50.

What Is Double-Dabble?

The fastest way to convert a binary number to decimal is a method called double-dabble (or double-dibble). This method builds on the idea that a subsequent power of two is double the previous power of two in a binary number. The calculation starts with the leftmost bit and works toward the rightmost bit. The first bit is doubled and added to the next bit. This sum is then doubled and added to the following bit. The process is repeated for each bit until the rightmost bit has been used.

Example 1

Convert: 10010011₂ to decimal.

Step 1: Write down the binary number, leaving space between the bits.

Step 2: Double the high-order bit and copy it under the next bit.

Step 3: Add the next bit and double the sum. Copy this result under the next bit.

Step 4: Repeat Step 3 until you run out of bits.

When we combine hextet grouping (in reverse) with the double-dabble method, we find that we can convert hexadecimal to decimal with ease.

Example 2

Convert: 02CA₁₆ to decimal.

First, convert the hex to binary by grouping into hextets.

Then apply the double-dabble method on the binary form:

As with addition, signed-magnitude subtraction is carried out in a manner similar to pencil and paper decimal arithmetic, where it is sometimes necessary to borrow from digits in the minuend.

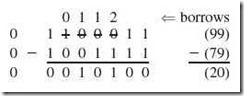
Example 2.12:

Subtract 01001111₂ from 01100011₂ using signed-magnitude arithmetic.

We find 01100011₂ – 01001111₂ = 00010100₂ in signed-magnitude representation.

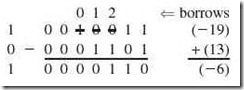
Example 2.13:

Subtract 01100011₂ (99) from 01001111₂ (79) using signedmagnitude arithmetic.

By inspection, we see that the subtrahend, 01100011, is larger than the minuend, 01001111. With the result obtained in Example 2.12, we know that the difference of these two numbers is 0010100₂. Because the subtrahend is larger than the minuend, all that we need to do is change the sign of the difference. So we find 01001111₂ – 01100011₂ = 10010100₂ in signed-magnitude representation.

We know that subtraction is the same as “adding the opposite,” which equates to negating the value we wish to subtract and then adding instead (which is often much easier than performing all the borrows necessary for subtraction, particularly in dealing with binary numbers). Therefore, we need to look at some examples involving both positive and negative numbers. Recall the rules for addition: (1) If the signs are the same, add the magnitudes and use that same sign for the result; (2) If the signs differ, you must determine which operand has the larger magnitude. The sign of the result is the same as the sign of the operand with the larger magnitude, and the magnitude must be obtained by subtracting (not adding) the smaller one from the larger one.

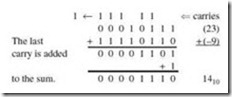
Example 2.14:

Add 10010011₂ (–19) to 00001101₂ (+13) using signed-magnitude arithmetic.

The first number (the augend) is negative because its sign bit is set to 1. The second number (the addend) is positive. What we are asked to do is in fact a subtraction. First, we determine which of the two numbers is larger in magnitude and use that number for the augend. Its sign will be the sign of the result.

With the inclusion of the sign bit, we see that 10010011₂ – 00001101₂ = 10000110₂ in signed-magnitude representation.

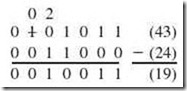
Example 2.15:

Subtract 10011000₂ (–24) from 10101011₂ (–43) using signed-magnitude arithmetic.

We can convert the subtraction to an addition by negating –24, which gives us 24, and then we can add this to –43, giving us a new problem of –43 + 24. However, we know from the addition rules above that because the signs now differ, we must actually subtract the smaller magnitude from the larger magnitude (or subtract 24 from 43) and make the result negative (since 43 is larger than 24).

Note that we are not concerned with the sign until we have performed the subtraction. We know the answer must be positive. So we end up with 10101011₂– 10001100₂ = 00010011₂ in signed-magnitude representation.

While reading the preceding examples, you may have noticed how many questions we had to ask ourselves: Which number is larger? Am I subtracting a negative number? How many times do I have to borrow from the minuend? A computer engineered to perform arithmetic in this manner must make just as many decisions (though a whole lot faster). The logic (and circuitry) is further complicated by the fact that signed magnitude has two representations for zero, 10000000 and 00000000 (and mathematically speaking, this simply shouldn’t happen!). Simpler methods for representing signed numbers would allow simpler and less expensive circuits. These simpler methods are based on radix complement systems.

2.4.2 Complement Systems

Number theorists have known for hundreds of years that one decimal number can be subtracted from another by adding the difference of the subtrahend from all nines and adding back a carry. This is called taking the nine’s complement of the subtrahend, or more formally, finding the diminished radix complement of the subtrahend. Let’s say we wanted to find 167 – 52. Taking the difference of 52 from 999, we have 947. Thus, in nine’s complement arithmetic we have 167 – 52 = 167 + 947 = 114. The “carry” from the hundreds column is added back to the units place, giving us a correct 167 – 52 = 115. This method was commonly called “casting out 9s” and has been extended to binary operations to simplify computer arithmetic. The advantage that complement systems give us over signed magnitude is that there is no need to process sign bits separately, but we can still easily check the sign of a number by looking at its high-order bit.

Another way to envision complement systems is to imagine an odometer on a bicycle. Unlike cars, when you go backward on a bike, the odometer will go backward as well. Assuming an odometer with three digits, if we start at zero and end with 700, we can’t be sure whether the bike went forward 700 miles or backward 300 miles! The easiest solution to this dilemma is simply to cut the number space in half and use 001–500 for positive miles and 501–999 for negative miles. We have, effectively, cut down the distance our odometer can measure. But now if it reads 997, we know the bike has backed up 3 miles instead of riding forward 997 miles. The numbers 501–999 represent the radix complements (the second of the two methods introduced below) of the numbers 001–500 and are being used to represent negative distance.

One’s Complement

As illustrated above, the diminished radix complement of a number in base 10 is found by subtracting the subtrahend from the base minus one, which is 9 in decimal. More formally, given a number N in base r having d digits, the diminished radix complement of N is defined to be (r^d – 1) N. For decimal numbers, r = 10, and the diminished radix is 10 – 1 = 9. For example, the nine’s complement of 2468 is 9999 2468 = 7531. For an equivalent operation in binary, we subtract from one less the base (2), which is 1. For example, the one’s complement of 0101₂ is 1111₂ – 0101 = 1010. Although we could tediously borrow and subtract as discussed above, a few experiments will convince you that forming the one’s complement of a binary number amounts to nothing more than switching all of the 1s with 0s and vice versa. This sort of bit-flipping is very simple to implement in computer hardware.

It is important to note at this point that although we can find the nine’s complement of any decimal number or the one’s complement of any binary number, we are most interested in using complement notation to represent negative numbers. We know that performing a subtraction, such as 10 – 7, can be also be thought of as “adding the opposite,” as in 10 + (–7). Complement notation allows us to simplify subtraction by turning it into addition, but it also gives us a method to represent negative numbers. Because we do not wish to use a special bit to represent the sign (as we did in signed-magnitude representation), we need to remember that if a number is negative, we should convert it to its complement. The result should have a 1 in the leftmost bit position to indicate the number is negative. If the number is positive, we do not have to convert it to its complement. All positive numbers should have a zero in the leftmost bit position. Example 2.16 illustrates these concepts.

Example 2.16:

Express 23₁₀ and 9₁₀ in 8-bit binary one’s complement form.

23₁₀ = + (00010111₂) = 00010111₂

9₁₀ = – (00001001₂) = 11110110₂

Suppose we wish to subtract 9 from 23. To carry out a one’s complement subtraction, we first express the subtrahend (9) in one’s complement, then add it to the minuend (23); we are effectively now adding 9 to 23. The high-order bit will have a 1 or a 0 carry, which is added to the low-order bit of the sum. (This is called end carry-around and results from using the diminished radix complement.)

Example 2.17:

Add 23₁₀ to –9₁₀ using one’s complement arithmetic.

Example 2.18:

Add 9₁₀ to –23₁₀ using one’s complement arithmetic.

How do we know that 11110001₂ is actually 14₁₀? We simply need to take the one’s complement of this binary number (remembering it must be negative because the leftmost bit is negative). The one’s complement of 11110001₂ is 00001110₂, which is 14.

The primary disadvantage of one’s complement is that we still have two representations for zero: 00000000 and 11111111. For this and other reasons, computer engineers long ago stopped using one’s complement in favor of the more efficient two’s complement representation for binary numbers.

Two’s Complement

Two’s complement is an example of a radix complement. Given a number N in base r having d digits, the radix complement of N is defined to be r^d– N for N ¹ 0and0for N = 0. The radix complement is often more intuitive than the diminished radix complement. Using our odometer example, the ten’s complement of going forward 2 miles is 10² – 2 = 998, which we have already agreed indicates a negative (backward) distance. Similarly, in binary, the two’s complement of the 4-bit number 0011₂ is 2⁴ – 0011₂ = 10000₂– 0011₂ = 1101₂.

Upon closer examination, you will discover that two’s complement is nothing more than one’s complement incremented by 1. To find the two’s complement of a binary number, simply flip bits and add 1. This simplifies addition and subtraction as well. Since the subtrahend (the number we complement and add) is incremented at the outset, however, there is no end carry-around to worry about. We simply discard any carries involving the high-order bits. Remember, only negative numbers need to be converted to two’s complement notation, as indicated in Example 2.19.

Example 2.19:

Express 23₁₀, –23₁₀, and –9₁₀ in 8-bit binary two’s complement form.

Suppose we are given the binary representation for a number and want to know its decimal equivalent? Positive numbers are easy. For example, to convert the two’s complement value of 00010111₂ to decimal, we simply convert this binary number to a decimal number to get 23. However, converting two’s complement negative numbers requires a reverse procedure similar to the conversion from decimal to binary. Suppose we are given the two’s complement binary value of 11110111₂, and we want to know the decimal equivalent. We know this is a negative number but must remember it is represented using two’s complement. We first flip the bits and then add 1 (find the one’s complement and add 1). This results in the following: 00001000₂ + 1 = 00001001₂. This is equivalent to the decimal value 9. However, the original number we started with was negative, so we end up with –9 as the decimal equivalent to 11110111₂.

The following two examples illustrate how to perform addition (and hence subtraction, because we subtract a number by adding its opposite) using two’s complement notation.

Example 2.20:

Add 9₁₀ to –23₁₀ using two’s complement arithmetic.

It is left as an exercise for you to verify that 11110010₂ is actually –14₁₀ using two’s complement notation.

Example 2.21:

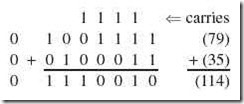
Find the sum of 23₁₀ and –9₁₀ in binary using two’s complement arithmetic.

Notice that the discarded carry in Example 2.21 did not cause an erroneous result. An overflow occurs if two positive numbers are added and the result is negative, or if two negative numbers are added and the result is positive. It is not possible to have overflow when using two’s complement notation if a positive and a negative number are being added together.

Simple computer circuits can easily detect an overflow condition using a rule that is easy to remember. You’ll notice in Example 2.21 that the carry going into the sign bit (a 1 is carried from the previous bit position into the sign bit position) is the same as the carry going out of the sign bit (a 1 is carried out and discarded). When these carries are equal, no overflow occurs. When they differ, an overflow indicator is set in the arithmetic logic unit, indicating the result is incorrect.

A Simple Rule for Detecting an Overflow Condition: If the carry into the sign bit equals the carry out of the bit, no overflow has occurred. If the carry into the sign bit is different from the carry out of the sign bit, overflow (and thus an error) has occurred.

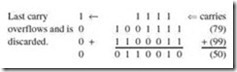
The hard part is getting programmers (or compilers) to consistently check for the overflow condition. Example 2.22 indicates overflow because the carry into the sign bit (a 1 is carried in) is not equal to the carry out of the sign bit (a 0 is carried out).

Example 2.22:

Find the sum of 126₁₀ and 8₁₀ in binary using two’s complement arithmetic.

Integer Multiplication And Division

Unless sophisticated algorithms are used, multiplication and division can consume a considerable number of computation cycles before a result is obtained. Here, we discuss only the most straightforward approach to these operations. In real systems, dedicated hardware is used to optimize throughput, sometimes carrying out portions of the calculation in parallel. Curious readers will want to investigate some of these advanced methods in the references cited at the end of this chapter.

The simplest multiplication algorithms used by computers are similar to traditional pencil and paper methods used by humans. The complete multiplication table for binary numbers couldn’t be simpler: zero times any number is zero, and one times any number is that number.

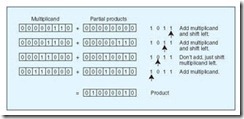
To illustrate simple computer multiplication, we begin by writing the multiplicand and the multiplier to two separate storage areas. We also need a third storage area for the product. Starting with the low-order bit, a pointer is set to each digit of the multiplier. For each digit in the multiplier, the multiplicand is “shifted” one bit to the left. When the multiplier is 1, the “shifted” multiplicand is added to a running sum of partial products. Because we shift the multiplicand by one bit for each bit in the multiplier, a product requires double the working space of either the multiplicand or the multiplier.

There are two simple approaches to binary division: We can either iteratively subtract the denominator from the divisor, or we can use the same trial-and-error method of long division that we were taught in grade school. As mentioned above with multiplication, the most efficient methods used for binary division are beyond the scope of this text and can be found in the references at the end of this chapter.

Regardless of the relative efficiency of any algorithms that are used, division is an operation that can always cause a computer to crash. This is the case particularly when division by zero is attempted or when two numbers of enormously different magnitudes are used as operands. When the divisor is much smaller than the dividend, we get a condition known as divide underflow, which the computer sees as the equivalent of division by zero, which is impossible.

Computers make a distinction between integer division and floating-point division. With integer division, the answer comes in two parts: a quotient and a remainder. Floating-point division results in a number that is expressed as a binary fraction. These two types of division are sufficiently different from each other as to warrant giving each its own special circuitry. Floating-point calculations are carried out in dedicated circuits called floating-point units, or FPUs.

Example Find the product of 00000110₂ and 00001011₂.

A one is carried into the leftmost bit, but a zero is carried out. Because these carries are not equal, an overflow has occurred. (We can easily see that two positive numbers are being added but the result is negative.)

Two’s complement is the most popular choice for representing signed numbers. The algorithm for adding and subtracting is quite easy, has the best representation for 0 (all 0 bits), is self-inverting, and is easily extended to larger numbers of bits. The biggest drawback is in the asymmetry seen in the range of values that can be represented by N bits. With signed-magnitude numbers, for example, 4 bits allow us to represent the values –7 through +7. However, using two’s complement, we can represent the values 8 through +7, which is often confusing to anyone learning about complement representations. To see why +7 is the largest number we can represent using 4-bit two’s complement representation, we need only remember the first bit must be 0. If the remaining bits are all 1s (giving us the largest magnitude possible), we have 0111₂, which is 7. An immediate reaction to this is that the smallest negative number should then be 1111₂, but we can see that 1111₂ is actually –1 (flip the bits, add one, and make the number negative). So how do we represent –8 in two’s complement notation using 4 bits? It is represented as 1000₂. We know this is a negative number. If we flip the bits (0111), add 1 (to get 1000, which is 8), and make it negative, we get –8.

2.5 Floating-Point Representation

If we wanted to build a real computer, we could use any of the integer representations that we just studied. We would pick one of them and proceed with our design tasks. Our next step would be to decide the word size of our system. If we want our system to be really inexpensive, we would pick a small word size, say 16 bits. Allowing for the sign bit, the largest integer that this system can store is 32,767. So now what do we do to accommodate a potential customer who wants to keep a tally of the number of spectators paying admission to professional sports events in a given year? Certainly, the number is larger than 32,767. No problem. Let’s just make the word size larger. Thirty-two bits ought to do it. Our word is now big enough for just about anything that anyone wants to count. But what if this customer also needs to know the amount of money each spectator spends per minute of playing time? This number is likely to be a decimal fraction. Now we’re really stuck.

The easiest and cheapest approach to this problem is to keep our 16-bit system and say, “Hey, we’re building a cheap system here. If you want to do fancy things with it, get yourself a good programmer.” Although this position sounds outrageously flippant in the context of today’s technology, it was a reality in the earliest days of each generation of computers. There simply was no such thing as a floating-point unit in many of the first mainframes or microcomputers. For many years, clever programming enabled these integer systems to act as if they were, in fact, floating-point systems.

If you are familiar with scientific notation, you may already be thinking of how you could handle floating-point operations—how you could provide floating-point emulation—in an integer system. In scientific notation, numbers are expressed in two parts: a fractional part, called a mantissa, and an exponential part that indicates the power of ten to which the mantissa should be raised to obtain the value we need. So to express 32,767 in scientific notation, we could write 3.2767 x 10⁴. Scientific notation simplifies pencil and paper calculations that involve very large or very small numbers. It is also the basis for floating-point computation in today’s digital computers.

2.5.1 A Simple Model

In digital computers, floating-point numbers consist of three parts: a sign bit, an exponent part (representing the exponent on a power of 2), and a fractional part called a significand (which is a fancy word for a mantissa). The number of bits used for the exponent and significand depends on whether we would like to optimize for range (more bits in the exponent) or precision (more bits in the significand). For the remainder of this section, we will use a 14-bit model with a 5-bit exponent, an 8-bit significand, and a sign bit (see Figure 2.2). More general forms are described in Section 2.5.2.

Let’s say that we wish to store the decimal number 17 in our model. We know that 17 = 17.0 x 10⁰ = 1.7 x 10¹ = 0.17 x 10². Analogously, in binary, 17₁₀ = 10001₂ x 2⁰ = 1000.1₂ x 2¹ = 100.01₂ x 2² = 10.001₂ x 2³ = 1.0001₂ x 2⁴ = 0.10001₂ x 2⁵. If we use this last form, our fractional part will be 10001000 and our exponent will be 00101, as shown here:

Using this form, we can store numbers of much greater magnitude than we could using a fixed-point representation of 14 bits (which uses a total of 14 binary digits plus a binary, or radix, point). If we want to represent 65536 = 0.1₂ x 2¹⁷in this model, we have:

One obvious problem with this model is that we haven’t provided for negative exponents. If we wanted to store 0.25 we would have no way of doing so because 0.25 is 2^{– 2} and the exponent –2 cannot be represented. We could fix the problem by adding a sign bit to the exponent, but it turns out that it is more efficient to use a biased exponent, because we can use simpler integer circuits when comparing the values of two floating-point numbers.

The idea behind using a bias value is to convert every integer in the range into a non-negative integer, which is then stored as a binary numeral. The integers in the desired range of exponents are first adjusted by adding this fixed bias value to each exponent. The bias value is a number near the middle of the range of possible values that we select to represent zero. In this case, we could select 16 because it is midway between 0 and 31 (our exponent has 5 bits, thus allowing for 2⁵ or 32 values). Any number larger than 16 in the exponent field will represent a positive value. Values less than 16 will indicate negative values. This is called an excess-16 representation because we have to subtract 16 to get the true value of the exponent. Note that exponents of all zeros or all ones are typically reserved for special numbers (such as zero or infinity).

Returning to our example of storing 17, we calculated 17₁₀ = 0.10001₂ x 2⁵. The biased exponent is now 16 + 5 = 21:

If we wanted to store 0.25 = 1.0 x 2^-2 we would have:

There is still one rather large problem with this system: We do not have a unique representation for each number. All of the following are equivalent:

Because synonymous forms such as these are not well-suited for digital computers, a convention has been established where the leftmost bit of the significand will always be a 1. This is called normalization. This convention has the additional advantage in that the 1 can be implied, effectively giving an extra bit of precision in the significand.

Example 2.23:

Express 0.03125₁₀ in normalized floating-point form with excess-16 bias.

0.03125₁₀ = 0.00001₂ x 2⁰ = 0.0001 x 2^{– 1} = 0.001 x 2^{– 2} = 0.01 x 2^{– 3} = 0.1 x 2^{– 4}. Applying the bias, the exponent field is 16 – 4 = 12.

Note that in this example we have not expressed the number using the normalization notation that implies the 1.

2.5.2 Floating-Point Arithmetic

If we wanted to add two decimal numbers that are expressed in scientific notation, such as 1.5 x 10² + 3.5 x 10³, we would change one of the numbers so that both of them are expressed in the same power of the base. In our example, 1.5 x 10² + 3.5 x 10³ = 0.15 x 10³ + 3.5 x 10³ = 3.65 x 10³. Floating-point addition and subtraction work the same way, as illustrated below.

Example 2.24:

Add the following binary numbers as represented in a normalized 14-bit format with a bias of 16.

We see that the addend is raised to the second power and that the augend is to the zero power. Alignment of these two operands on the binary point gives us:

Renormalizing, we retain the larger exponent and truncate the low-order bit. Thus, we have:

Multiplication and division are carried out using the same rules of exponents applied to decimal arithmetic, such as 2^{– 3} x 2⁴= 2¹, for example.

Example 2.25:

Multiply:

Multiplication of 0.11001000 by 0.10011010 yields a product of 1.11011011. Renormalizing and supplying the appropriate exponent, the floating-point product is:

2.5.3 Floating-Point Errors

When we use pencil and paper to solve a trigonometry problem or compute the interest on an investment, we intuitively understand that we are working in the system of real numbers. We know that this system is infinite, because given any pair of real numbers, we can always find another real number that is smaller than one and greater than the other.

Unlike the mathematics in our imaginations, computers are finite systems, with finite storage. When we call upon our computers to carry out floating-point calculations, we are modeling the infinite system of real numbers in a finite system of integers. What we have, in truth, is an approximation of the real number system. The more bits we use, the better the approximation. However, there is always some element of error, no matter how many bits we use.

Floating-point errors can be blatant, subtle, or unnoticed. The blatant errors, such as numeric overflow or underflow, are the ones that cause programs to crash. Subtle errors can lead to wildly erroneous results that are often hard to detect before they cause real problems. For example, in our simple model, we can express normalized numbers in the range of .11111111₂ x 2¹⁵ through +.11111111 x 2¹⁵. Obviously, we cannot store 2 ^{– 19} or 2¹²⁸; they simply don’t fit. It is not quite so obvious that we cannot accurately store 128.5, which is well within our range. Converting 128.5 to binary, we have 10000000.1, which is 9 bits wide. Our significand can hold only eight. Typically, the low-order bit is dropped or rounded into the next bit. No matter how we handle it, however, we have introduced an error into our system.

We can compute the relative error in our representation by taking the ratio of the absolute value of the error to the true value of the number. Using our example of 128.5, we find:

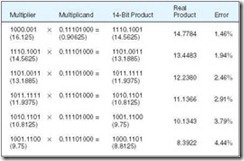
If we are not careful, such errors can propagate through a lengthy calculation, causing substantial loss of precision. Figure 2.3 illustrates the error propagation as we iteratively multiply 16.24 by 0.91 using our 14-bit model. Upon converting these numbers to 8-bit binary, we see that we have a substantial error from the outset.

Figure 2.3: Error Propagation in a 14-Bit Floating-Point Number

As you can see, in six iterations, we have more than tripled the error in the product. Continued iterations will produce an error of 100% because the product eventually goes to zero. Although this 14-bit model is so small that it exaggerates the error, all floating-point systems behave the same way. There is always some degree of error involved when representing real numbers in a finite system, no matter how large we make that system. Even the smallest error can have catastrophic results, particularly when computers are used to control physical events such as in military and medical applications. The challenge to computer scientists is to find efficient algorithms for controlling such errors within the bounds of performance and economics.

2.5.4 The IEEE-754 Floating-Point Standard

The floating-point model that we have been using in this section is designed for simplicity and conceptual understanding. We could extend this model to include whatever number of bits we wanted. Until the 1980s, these kinds of decisions were purely arbitrary, resulting in numerous incompatible representations across various manufacturers’ systems. In 1985, the Institute of Electrical and Electronic Engineers (IEEE) published a floating-point standard for both singleand double-precision floating-point numbers. This standard is officially known as IEEE-754 (1985).

The IEEE-754 single-precision standard uses an excess 127 bias over an 8-bit exponent. The significand is 23 bits. With the sign bit included, the total word size is 32 bits. When the exponent is 255, the quantity represented is infinity (which has a zero significand) or “not a number” (which has a non-zero significand). “Not a number,” or NaN, is used to represent a value that is not a real number and is often used as an error indicator.

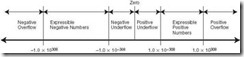
Double-precision numbers use a signed 64-bit word consisting of an 11-bit exponent and 52-bit significand. The bias is 1023. The range of numbers that can be represented in the IEEE double-precision model is shown in Figure 2.4. NaN is indicated when the exponent is 2047.

Figure 2.4: Range of IEEE-754 Double-Precision Numbers

At a slight cost in performance, most FPUs use only the 64-bit model so that only one set of specialized circuits needs to be designed and implemented.

Both the single-precision and double-precision IEEE-754 models have two representations for zero. When the exponent and the significand are both all zero, the quantity stored is zero. It doesn’t matter what value is stored in the sign. For this reason, programmers should use caution when comparing a floating-point value to zero.

Virtually every recently designed computer system has adopted the IEEE-754 floating-point model. Unfortunately, by the time this standard came along, many mainframe computer systems had established their own floating-point systems. Changing to the newer system has taken decades for well-established architectures such as IBM mainframes, which now support both their traditional floating-point system and IEEE-754. Before 1998, however, IBM systems had been using the same architecture for floating-point arithmetic that the original System/360 used in 1964. One would expect that both systems will continue to be supported, owing to the substantial amount of older software that is running on these systems.

2.6 Character Codes

We have seen how digital computers use the binary system to represent and manipulate numeric values. We have yet to consider how these internal values can be converted to a form that is meaningful to humans. The manner in which this is done depends on both the coding system used by the computer and how the values are stored and retrieved.

2.6.1 Binary-Coded Decimal

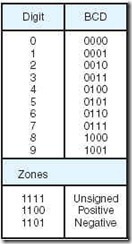
Binary-coded decimal (BCD) is a numeric coding system used primarily in IBM mainframe and midrange systems. As its name implies, BCD encodes each digit of a decimal number to a 4-bit binary form. When stored in an 8-bit byte, the upper nibble is called the zone and the lower part is called the digit. (This convention comes to us from the days of punched cards where each column of the card could have a “zone punch” in one of the top 2 rows and a “digit punch” in one of the 10 bottom rows.) The high-order nibble in a BCD byte is used to hold the sign, which can have one of three values: An unsigned number is indicated with 1111; a positive number is indicated with 1100; and a negative number is indicated with 1101. Coding for BCD numbers is shown in Figure 2.5.

Figure 2.5: Binary-Coded Decimal

As you can see by the figure, six possible binary values are not used, 1010 through 1111. Although it may appear that nearly 40% of our values are going to waste, we are gaining a considerable advantage in accuracy. For example, the number 0.3 is a repeating decimal when stored in binary. Truncated to an 8-bit fraction, it converts back to 0.296875, giving us an error of approximately 1.05%. In BCD, the number is stored directly as 1111 0011 (we are assuming the decimal point is implied by the data format), giving no error at all.

The digits of BCD numbers occupy only one nibble, so we can save on space and make computations simpler when adjacent digits are placed into adjacent nibbles, leaving one nibble for the sign. This process is known as packing and numbers thus stored are called packed decimal numbers.

Example 2.26:

Represent –1265 in 3 bytes using packed BCD.

The zoned-decimal coding for 1265 is:

1111 0001 1111 0010 1111 0110 1111 0101

After packing, this string becomes:

0001 0010 0110 0101

Adding the sign after the low-order digit and padding the high-order digit with ones in 3 bytes we have:

2.6.2 EBCDIC

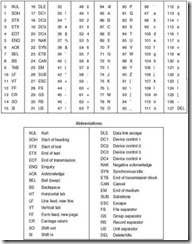
Before the development of the IBM System/360, IBM had used a 6-bit variation of BCD for representing characters and numbers. This code was severely limited in how it could represent and manipulate data; in fact, lowercase letters were not part of its repertoire. The designers of the System/360 needed more information processing capability as well as a uniform manner in which to store both numbers and data. In order to maintain compatibility with earlier computers and peripheral equipment, the IBM engineers decided that it would be best to simply expand BCD from 6 bits to 8 bits. Accordingly, this new code was called Extended Binary Coded Decimal Interchange Code (EBCDIC). IBM continues to use EBCDIC in IBM mainframe and midrange computer systems. The EBCDIC code is shown in Figure 2.6 in zone-digit form. Characters are represented by appending digit bits to zone bits. For example, the character a is 1000 0001 and the digit 3 is 1111 0011 in EBCDIC. Note the only difference between upperand lowercase characters is in bit position 2, making a translation from upperto lowercase (or vice versa) a simple matter of flipping one bit. Zone bits also make it easier for a programmer to test the validity of input data.

Figure 2.6: The EBCDIC Code (Values Given in Binary Zone-Digit Format)

2.6.3 ASCII

While IBM was busy building its iconoclastic System/360, other equipment makers were trying to devise better ways for transmitting data between systems. The American Standard Code for Information Interchange (ASCII) is one outcome of these efforts. ASCII is a direct descendant of the coding schemes used for decades by teletype (telex) devices. These devices used a 5-bit (Murray) code that was derived from the Baudot code, which was invented in the 1880s. By the early 1960s, the limitations of the 5-bit codes were becoming apparent. The International Organization for Standardization (ISO) devised a 7-bit coding scheme that it called International Alphabet Number 5. In 1967, a derivative of this alphabet became the official standard that we now call ASCII.

As you can see in Figure 2.7, ASCII defines codes for 32 control characters, 10 digits, 52 letters (upperand lowercase), 32 special characters (such as $ and #), and the space character. The high-order (eighth) bit was intended to be used for parity.

Figure 2.7: The ASCII Code (Values Given in Decimal)

Parity is the most basic of all error detection schemes. It is easy to implement in simple devices like teletypes. A parity bit is turned “on” or “off” depending on whether the sum of the other bits in the byte is even or odd. For example, if we decide to use even parity and we are sending an ASCII A, the lower 7 bits are 1000001. Because the sum of the bits is even, the parity bit would be set to off and we would transmit 0100 0001. Similarly, if we transmit an ASCII C, 100 0011, the parity bit would be set to on before we sent the 8-bit byte, 1100 0011. Parity can be used to detect only single-bit errors. We will discuss more sophisticated error detection methods in Section 2.8.

To allow compatibility with telecommunications equipment, computer manufacturers gravitated toward the ASCII code. As computer hardware became more reliable, however, the need for a parity bit began to fade. In the early 1980s, microcomputer and microcomputer-peripheral makers began to use the parity bit to provide an “extended” character set for values between 128₁₀ and 255_10.

Depending on the manufacturer, the higher-valued characters could be anything from mathematical symbols to characters that form the sides of boxes to foreign-language characters such as ñ. Unfortunately, no amount of clever tricks can make ASCII a truly international interchange code.

2.6.4 Unicode

Both EBCDIC and ASCII were built around the Latin alphabet. As such, they are restricted in their abilities to provide data representation for the non-Latin alphabets used by the majority of the world’s population. As all countries began using computers, each was devising codes that would most effectively represent their native languages. None of these were necessarily compatible with any others, placing yet another barrier in the way of the emerging global economy.

In 1991, before things got too far out of hand, a consortium of industry and public leaders was formed to establish a new international information exchange code called Unicode. This group is appropriately called the Unicode Consortium.

Unicode is a 16-bit alphabet that is downward compatible with ASCII and the Latin-1 character set. It is conformant with the ISO/IEC 10646-1 international alphabet. Because the base coding of Unicode is 16 bits, it has the capacity to encode the majority of characters used in every language of the world. If this weren’t enough, Unicode also defines an extension mechanism that will allow for the coding of an additional million characters. This is sufficient to provide codes for every written language in the history of civilization.

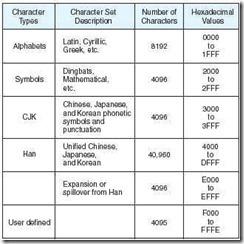
The Unicode codespace consists of five parts, as shown in Figure 2.8. A full Unicode-compliant system will also allow formation of composite characters from the individual codes, such as the combination of ´ and A to form Á. The algorithms used for these composite characters, as well as the Unicode extensions, can be found in the references at the end of this chapter.

Figure 2.8: Unicode Codespace

Although Unicode has yet to become the exclusive alphabet of American computers, most manufacturers are including at least some limited support for it in their systems. Unicode is currently the default character set of the Java programming language. Ultimately, the acceptance of Unicode by all manufacturers will depend on how aggressively they wish to position themselves as international players and how inexpensively disk drives can be produced to support an alphabet with double the storage requirements of ASCII or EBCDIC.

2.7 Codes For Data Recording And Transmission

ASCII, EBCDIC, and Unicode are represented unambiguously in computer memories. (Chapter 3 describes how this is done using binary digital devices.) Digital switches, such as those used in memories, are either “off” or “on” with nothing in between. However, when data is written to some sort of recording medium (such as tape or disk), or transmitted over long distances, binary signals can become blurred, particularly when long strings of ones and zeros are involved. This blurring is partly attributable to timing drifts that occur between senders and receivers. Magnetic media, such as tapes and disks, can also lose synchronization owing to the electrical behavior of the magnetic material from which they are made. Signal transitions between the “high” and “low” states of digital signals help to maintain synchronization in data recording and communications devices. To this end, ASCII, EBCDIC, and Unicode are translated into other codes before they are transmitted or recorded. This translation is carried out by control electronics within data recording and transmission devices. Neither the user nor the host computer is ever aware that this translation has taken place.

Bytes are sent and received by telecommunications devices by using “high” and “low” pulses in the transmission media (copper wire, for example). Magnetic storage devices record data using changes in magnetic polarity called flux reversals. Certain coding methods are better suited for data communications than for data recording. New codes are continually being invented to accommodate evolving recording methods and improved transmission and recording media. We will examine a few of the more popular recording and transmission codes to show how some of the challenges in this area have been overcome. For the sake of brevity, we will use the term data encoding to mean the process of converting a simple character code such as ASCII to some other code that better lends itself to storage or transmission. Encoded data will be used to refer to character codes so encoded.

2.7.1 Non-Return-to-Zero Code

The simplest data encoding method is the non-return-to-zero (NRZ) code. We use this code implicitly when we say that “highs” and “lows” represent ones and zeros: ones are usually high voltage, and zeroes are low voltage. Typically, high voltage is positive 3 or 5 volts; low voltage is negative 3 or 5 volts. (The reverse is logically equivalent.)

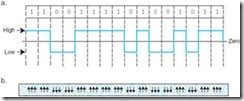
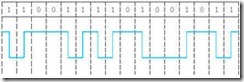
For example, the ASCII code for the English word OK with even parity is: 11001111 01001011. This pattern in NRZ code is shown in its signal form as well as in its magnetic flux form in Figure 2.9. Each of the bits occupies an arbitrary slice of time in a transmission medium or an arbitrary speck of space on a disk. These slices and specks are called bit cells.

Figure 2.9: NRZ Encoding of OK as
a. Transmission Waveform
b. Magnetic Flux Pattern (The direction of the arrows indicates the magnetic polarity.)

As you can see by the figure, we have a long run of ones in the ASCII O. If we transmit the longer form of the word OK, OKAY, we would have a long string of zeros as well as a long string of ones: 11001111 01001011 01000001 01011001. Unless the receiver is synchronized precisely with the sender, it is not possible for either to know the exact duration of the signal for each bit cell. Slow or out-of-phase timing within the receiver might cause the bit sequence for OKAY to be received as: 10011 0100101 010001 0101001, which would be translated back to ASCII as <ETX>(), bearing no resemblance to what was sent. (<ETX> is used here to mean the single ASCII End-of-Text character, 26 in decimal.)

A little experimentation with this example will demonstrate to you that if only one bit is missed in NRZ code, the entire message can be reduced to gibberish.

2.7.2 Non-Return-to-Zero-Invert Encoding

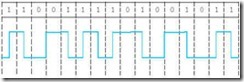
The non-return-to-zero-invert (NRZI) method addresses part of the problem of synchronization loss. NRZI provides a transition-either high-to-low or low-tohigh-for each binary one, and no transition for binary zero. The NRZI coding for OK (with even parity) is shown in Figure 2.10.

Although NRZI eliminates the problem of dropping binary ones, we are still faced with the problem of long strings of zeros causing the receiver or reader to drift out of phase, potentially dropping bits along the way.

The obvious approach to solving this problem is to inject sufficient transitions into the transmitted waveform to keep the sender and receiver synchronized, while preserving the information content of the message. This is the essential idea behind all coding methods used today in the storage and transmission of data.

2.7.3 Phase Modulation (Manchester Coding)

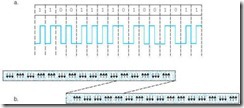
The coding method known commonly as phase modulation (PM), or Manchester coding, deals with the synchronization problem head-on. PM provides a transition for each bit, whether a one or a zero. In PM, each binary one is signaled by an “up” transition, and binary zeros with a “down” transition. Extra transitions are provided at bit cell boundaries when necessary. The PM coding of the word OK is shown in Figure 2.11.

Figure 2.11: Phase Modulation (Manchester Coding) of the Word OK as: a. Transmission Waveform b. Magnetic Flux Pattern

Phase modulation is often used in data transmission applications such as local area networks. It is inefficient for use in data storage, however. If PM were used for tape and disk, phase modulation would require twice the bit density of NRZ. (One flux transition for each half bit cell, depicted in Figure 2.11b.) However, we have just seen how using NRZ might result in unacceptably high error rates. We could therefore define a “good” encoding scheme as a method that most economically achieves a balance between “excessive” storage volume requirements and “excessive” error rates. A number of codes have been created in trying to find this middle ground.

2.7.4 Frequency Modulation

As used in digital applications, frequency modulation (FM) is similar to phase modulation in that at least one transition is supplied for each bit cell. These synchronizing transitions occur at the beginning of each bit cell. To encode a binary 1, an additional transition is provided in the center of the bit cell. The FM coding for OK is shown in Figure 2.12.

Figure 2.12: Frequency Modulation Coding of OK

As you can readily see from the figure, FM is only slightly better than PM with respect to its storage requirements. FM, however, lends itself to a coding method called modified frequency modulation (MFM), whereby bit cell boundary transitions are provided only between consecutive zeros. With MFM, then, at least one transition is supplied for every pair of bit cells, as opposed to each cell in PM or FM.

With fewer transitions than PM and more transitions than NRZ, MFM is a highly effective code in terms of economy and error control. For many years, MFM was virtually the only coding method used for rigid disk storage. The MFM coding for OK is shown in Figure 2.13.

Figure 2.13: Modified Frequency Modulation Coding of OK

2.7.5 Run-Length-Limited Code

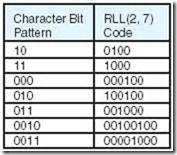
Run-length-limited (RLL) is a coding method in which block character code words such as ASCII or EBCDIC are translated into code words specially designed to limit the number of consecutive zeros appearing in the code. An RLL(d, k) code allows a minimum of d and a maximum of k consecutive zeros to appear between any pair of consecutive ones.

Clearly, RLL code words must contain more bits than the original character code. However, because RLL is coded using NRZI on the disk, RLL-coded data actually occupies less space on magnetic media because fewer flux transitions are involved. The code words employed by RLL are designed to prevent a disk from losing synchronization as it would if a “flat” binary NRZI code were used.

Although there are many variants, RLL(2, 7) is the predominant code used by magnetic disk systems. It is technically a 16-bit mapping of 8-bit ASCII or EBCDIC characters. However, it is nearly 50% more efficient than MFM in terms of flux reversals. (Proof of this is left as an exercise.)

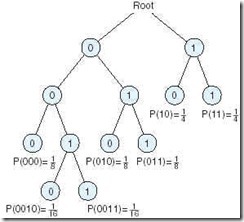
Theoretically speaking, RLL is a form of data compression called Huffman coding (discussed in Chapter 7), where the most likely information bit patterns are encoded using the shortest code word bit patterns. (In our case, we are talking about the fewest number of flux reversals.) The theory is based on the assumption that the presence or absence of a 1 in any bit cell is an equally likely event. From this assumption, we can infer that the probability is 0.25 of the pattern 10 occurring within any pair of adjacent bit cells.

Similarly, the bit pattern 011 has a probability of 0.125 of occurring. Figure 2.14 shows the probability tree for the bit patterns used in RLL(2, 7). Figure 2.15 gives the bit patterns used by RLL(2, 7).

Figure 2.14: The Probability Tree for RLL(2, 7) Coding

Figure 2.15: RLL(2, 7) Coding

As you can see by the table, it is impossible to have more than seven consecutive 0s, while at least two 0s will appear in any possible combination of bits.

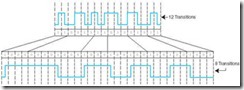
Figure 2.16 compares the MFM coding for OK with its RLL(2, 7) NRZI coding. MFM has 12 flux transitions to 8 transitions for RLL. If the limiting factor in the design of a disk is the number of flux transitions per square millimeter, we can pack 50% more OKs in the same magnetic area using RLL than we could using MFM. For this reason, RLL is used almost exclusively in the manufacture of high-capacity disk drives.

Figure 2.16: MFM (top) and RLL(2, 7) Coding (bottom) for OK

2.8 Error Detection And Correction

Regardless of the coding method used, no communications channel or storage medium can be completely error-free. It is a physical impossibility. As transmission rates are increased, bit timing gets tighter. As more bits are packed per square millimeter of storage, flux densities increase. Error rates increase in direct proportion to the number of bits per second transmitted, or the number of bits per square millimeter of magnetic storage.

In Section 2.6.3, we mentioned that a parity bit could be added to an ASCII byte to help determine whether any of the bits had become corrupted during transmission. This method of error detection is limited in its effectiveness: Simple parity can detect only an odd number of errors per byte. If two errors occur, we are helpless to detect a problem.

In Section 2.7.1, we showed how the 4-byte sequence for the word OKAY could be received as the 3-byte sequence <ETX>(). Alert readers noticed that the parity bits for the second sequence were correct, allowing nonsense to pass for good data. If such errors occur in sending financial information or program code, the effects can be disastrous.

As you read the sections that follow, you should keep in mind that just as it is impossible to create an error-free medium, it is also impossible to detect or correct 100% of all errors that could occur in a medium. Error detection and correction is yet another study in the tradeoffs that one must make in designing computer systems. The well-constructed error control system is therefore a system where a “reasonable” number of the “reasonably” expected errors can be detected or corrected within the bounds of “reasonable” economics. (Note: The word reasonable is implementation-dependent.)

2.8.1 Cyclic Redundancy Check

Checksums are used in a wide variety of coding systems, from bar codes to International Standard Book Numbers (ISBNs). These are self-checking codes that will quickly indicate whether the preceding digits have been misread. Cyclic redundancy check (CRC) is a type of checksum used primarily in data communications that determines whether an error has occurred within a large block or stream of information bytes. The larger the block to be checked, the larger the checksum must be to provide adequate protection. Checksums and CRCs are a type of systematic error detection scheme, meaning that the error-checking bits are appended to the original information byte. The group of error-checking bits is called a syndrome. The original information byte is unchanged by the addition of the error-checking bits.

The word cyclic in cyclic redundancy check refers to the abstract mathematical theory behind this error control system. Although a discussion of this theory is beyond the scope of this text, we can demonstrate how the method works to aid in your understanding of its power to economically detect transmission errors.

Arithmetic Modulo 2

You may be familiar with integer arithmetic taken over a modulus. Twelve-hour clock arithmetic is a modulo 12 system that you use every day to tell time. When we add 2 hours to 11:00, we get 1:00. Arithmetic modulo 2 uses two binary operands with no borrows or carries. The result is likewise binary and is also a member of the modulus 2 system. Because of this closure under addition, and the existence of identity elements, mathematicians say that this modulo 2 system forms an algebraic field.

The addition rules are as follows:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 0

Example 2.27:

Find the sum of 1011₂ and 110₂ modulo 2.

1011

+110

1101₂(mod 2)

This sum makes sense only in modulo 2.

Modulo 2 division operates through a series of partial sums using the modulo 2 addition rules. Example 2.28 illustrates the process.

Example 2.28:

Find the quotient and remainder when 1001011₂ is divided by 1011₂.

The quotient is 1010₂.

Arithmetic operations over the modulo 2 field have polynomial equivalents that are analogous to polynomials over the field of integers. We have seen how positional number systems represent numbers in increasing powers of a radix, for example,

1011₂ = 1 x 2³ + 0 x 2² + 1 x 2¹ + 1 x 2⁰.

By letting X = 2, the binary number 1011₂ becomes shorthand for the polynomial:

1 X³ + 0 X² + 1 X¹ + 1 X⁰.

The division performed in Example 2.28 then becomes the polynomial operation:

Calculating and Using CRCs

With that lengthy preamble behind us, we can now proceed to show how CRCs are constructed. We will do this by example:

Let the information byte I = 1001011₂. (Any number of bytes can be used to form a message block.)
The sender and receiver agree upon an arbitrary binary pattern, say P = 1011₂ . (Patterns beginning and ending with 1 work best.)
Shift I to the left by one less than the number of bits in P, giving a new I = 1001011000₂.
Using I as a dividend and P as a divisor, perform the modulo 2 division (as shown in Example 2.28). We ignore the quotient and note the remainder is 100₂. The remainder is the actual CRC checksum.
Add the remainder to I, giving the message M:

1001011000₂ + 100₂ = 1001011100₂
M is decoded and checked by the message receiver using the reverse process. Only now P divides M exactly:

A remainder other than zero indicates that an error has occurred in the transmission of M. This method works best when a large prime polynomial is used. There are four standard polynomials used widely for this purpose:

CRC-CCITT (ITU-T): X¹⁶ + X¹² + X⁵ + 1
CRC-12: X¹² + X¹¹ + X³ + X² + X + 1
CRC-16 (ANSI): X¹⁶ + X¹⁵ + X² + 1
CRC-32: X³² + X²⁶ + X²³ + X²² + X¹⁶ + X¹² + X¹¹ + X¹⁰ + X⁸ + X⁷ + X⁵ + X⁴ + X +1

CRC-CCITT, CRC-12, and CRC-16 operate over pairs of bytes; CRC-32 uses four bytes, which is appropriate for systems operating on 32-bit words. It has been proven that CRCs using these polynomials can detect over 99.8% of all single-bit errors.

CRCs can be implemented effectively using lookup tables as opposed to calculating the remainder with each byte. The remainder generated by each possible input bit pattern can be “burned” directly into communications and storage electronics. The remainder can then be retrieved using a 1-cycle lookup as compared to a 16 or 32-cycle division operation. Clearly, the tradeoff is in speed versus the cost of more complex control circuitry.

2.8.2 Hamming Codes

Data communications channels are simultaneously more error-prone and more tolerant of errors than disk systems. In data communications, it is sufficient to have only the ability to detect errors. If a communications device determines that a message contains an erroneous bit, all it has to do is request retransmission. Storage systems and memory do not have this luxury. A disk can sometimes be the sole repository of a financial transaction, or other collection of nonreproducible real-time data. Storage devices and memory must therefore have the ability to not only detect but to correct a reasonable number of errors.

Error-recovery coding has been studied intensively over the past century. One of the most effective codes-and the oldest-is the Hamming code. Hamming codes are an adaptation of the concept of parity, whereby error detection and correction capabilities are increased in proportion to the number of parity bits added to an information word. Hamming codes are used in situations where random errors are likely to occur. With random errors, we assume each bit failure has a fixed probability of occurrence independent of other bit failures. It is common for computer memory to experience such errors, so in our following discussion, we present Hamming codes in the context of memory bit error detection and correction.

We mentioned that Hamming codes use parity bits, also called check bits or redundant bits. The memory word itself consists of m bits, but r redundant bits are added to allow for error detection and/or correction. Thus, the final word, called a code word, is an n-bit unit containing m data bits and r check bits. There exists a unique code word consisting for n = m + r bits for each data word as follows:

The number of bit positions in which two code words differ is called the Hamming distance of those two code words. For example, if we have the following two code words:

we see that they differ in 3 bit positions, so the Hamming distance of these two code words is 3. (Please note that we have not yet discussed how to create code words; we do that shortly.)

The Hamming distance between two code words is important in the context of error detection. If two code words are a Hamming distance d apart, d single-bit errors are required to convert one code word to the other, which implies this type of error would not be detected. Therefore, if we wish to create a code that guarantees detection of all single-bit errors (an error in only 1 bit), all pairs of code words must have a Hamming distance of at least 2. If an n-bit word is not recognized as a legal code word, it is considered an error.

Given an algorithm for computing check bits, it is possible to construct a complete list of legal code words. The smallest Hamming distance found among all pairs of the code words in this code is called the minimum Hamming distance for the code. The minimum Hamming distance of a code, often signified by the notation D(min), determines its error detecting and correcting capability. Stated succinctly, for any code word X to be received as another valid code word Y, at least D(min) errors must occur in X. So, to detect k (or fewer) single-bit errors, the code must have a Hamming distance of D(min) = k + 1. Hamming codes can always detect D(min) 1 errors and correct (D(min) 1)/2 errors.¹ Accordingly, the Hamming distance of a code must be at least 2k + 1 in order for it to be able to correct k errors.

Code words are constructed from information words using r parity bits. Before we continue the discussion of error detection and correction, let’s consider a simple example. The most common error detection uses a single parity bit appended to the data (recall the discussion on ASCII character representation). A single-bit error in any bit of the code word produces the wrong parity.

Example 2.29:

Assume a memory with 2 data bits and 1 parity bit (appended at the end of the code word) that uses even parity (so the number of 1s in the codeword must be even). With 2 data bits, we have a total of 4 possible words. We list here the data word, its corresponding parity bit, and the resulting code word for each of these 4 possible words:

Data

Parity

Code

Word

Bit

Word

000

011

101

110

The resulting code words have 3 bits. However, using 3 bits allows for 8 different bit patterns, as follows (valid code words are marked with an *):

000^[*]

100

001

101^[*]

010

110^[*]

011^[*]

111

[*] The brackets denote the integer floor function, which is the largest integer that is smaller than the enclosed quantity. For example, [8.3] = 8 and [8.9] = 8.

If the code word 001 is encountered, it is invalid and thus indicates an error has occurred somewhere in the code word. For example, suppose the correct code word to be stored in memory is 011, but an error produces 001. This error can be detected, but it cannot be corrected. It is impossible to determine exactly how many bits have been flipped and exactly which ones are in error. Error-correcting codes require more than a single parity bit, as we see in the following discussion.

What happens in the above example if a valid code word is subject to two-bit errors? For example, suppose the code word 011 is converted into 000. This error is not detected. If you examine the code in the above example, you will see that D(min) is 2, which implies this code is guaranteed to detect only single bit errors.

We have already stated that the error detecting and correcting capabilities of a code are dependent on D(min), and, from an error detection point of view, we have seen this relationship exhibited in Example 2.29. Error correction requires the code to contain additional redundant bits to ensure a minimum Hamming distance D(min) =2k + 1 if the code is to detect and correct k errors. This Hamming distance guarantees that all legal code words are far enough apart that even with k changes, the original invalid code word is closer to one unique valid code word. This is important, because the method used in error correction is to change the invalid code word into the valid code word that differs in the fewest number of bits. This idea is illustrated in Example 2.30.

Listing 2.30:

Suppose we have the following code (do not worry at this time about how this code was generated; we address this issue shortly):

First, let’s determine D(min). By examining all possible pairs of code words, we discover that the minimum Hamming distance D(min) = 3. Thus, this code can detect up to two errors and correct one single bit error. How is correction handled? Suppose we read the invalid code word 10000. There must be at least one error because this does not match any of the valid code words. We now determine the Hamming distance between the observed code word and each legal code word: it differs in 1 bit from the first code word, 4 from the second, 2 from the third, and 3 from the last, resulting in a difference vector of [1,4,2,3]. To make the correction using this code, we automatically correct to the legal code word closest to the observed word, resulting in a correction to 00000. Note that this “correction” is not necessarily correct! We are assuming the minimum number of possible errors has occurred, namely 1. It is possible that the original code word was supposed to be 10110 and was changed to 10000 when two errors occurred.

Suppose two errors really did occur. For example, assume we read the invalid code word 11000. If we calculate the distance vector of [2,3,3,2], we see there is no “closest” code word, and we are unable to make the correction. The minimum Hamming distance of three permits correction of one error only, and cannot ensure correction, as evidenced in this example, if more than one error occurs.

In our discussion up to this point, we have simply presented you with various codes, but have not given any specifics as to how the codes are generated. There are many methods that are used for code generation; perhaps one of the more intuitive is the Hamming algorithm for code design, which we now present. Before explaining the actual steps in the algorithm, we provide some background material.

Suppose we wish to design a code with words consisting of m data bits and r check bits, which allows for single bit errors to be corrected. This implies there are 2^m legal code words, each with a unique combination of check bits. Since we are focused on single bit errors, let’s examine the set of invalid code words that are a distance of 1 from all legal code words.

Each valid code word has n bits, and an error could occur in any of these n positions. Thus, each valid code word has n illegal code words at a distance of 1. Therefore, if we are concerned with each legal code word and each invalid code word consisting of one error, we have n + 1 bit patterns associated with each code word (1 legal word and n illegal words). Since each code word consists of n bits, where n = m + r, there are 2ⁿ total bit patterns possible. This results in the following inequality:

(n + 1) x 2^m £ 2ⁿ

where n + 1 is the number of bit patterns per code word, 2^m is the number of legal code words, and 2ⁿ is the total number of bit patterns possible. Because n = m + r, we can rewrite the inequality as:

(m + r + 1) x 2^m £ 2^m r

(m + r + 1) £ 2^r

This inequality is important because it specifies the lower limit on the number of check bits required (we always use as few check bits as possible) to construct a code with m data bits and r check bits that corrects all single bit errors.

Suppose we have data words of length m = 4. Then:

(4 + r + 1) £ 2^r

which implies r must be greater than or equal to 3. We choose r = 3. This means to build a code with data words of 4 bits that should correct single bit errors, we must add 3 check bits.

The Hamming algorithm provides a straightforward method for designing codes to correct single bit errors. To construct error correcting codes for any size memory word, we follow these steps:

Determine the number of check bits, r, necessary for the code and then number the n bits (where n = m + r), right to left, starting with 1 (not 0)
Each bit whose bit number is a power of 2 is a parity bit-the others are data bits.
Assign parity bits to check bit positions as follows: Bit b is checked by those parity bits b₁, b₂, . . . , b_j such that b₁ + b₂ + . . . + b_j = b. (Where “+” indicates the modulo 2 sum.)

We now present an example to illustrate these steps and the actual process of error correction.

Example 2.31:

Using the Hamming code just described and even parity, encode the 8-bit ASCII character K. (The high-order bit will be zero.) Induce a single-bit error and then indicate how to locate the error.

We first determine the code word for K.

Step 1: Determine the number of necessary check bits, add these bits to the data bits, and number all n bits.

Since m = 8, we have: (8 + r + 1) £ 2^r, which implies r must be greater than or equal to 4. We choose r = 4.

Step 2: Number the n bits right to left, starting with 1, which results in:

Therefore, the code word for K is 010011010110.

Let’s introduce an error in bit position b₉, resulting in the code word 010111010110. If we use the parity bits to check the various sets of bits, we find the following:

Bit 1 checks 1, 3, 5, 7, 9, and 11: With even parity, this produces an error. Bit 2 checks 2, 3, 6, 7, 10, and 11: This is ok. Bit 4 checks 4, 5, 6, 7, and 12: This is ok. Bit 8 checks 8, 9, 10, 11, and 12: This produces an error.

Parity bits 1 and 8 show errors. These two parity bits both check 9 and 11, so the single bit error must be in either bit 9 or bit 11. However, since bit 2 checks bit 11 and indicates no error has occurred in the subset of bits it checks, the error must occur in bit 9. (We know this because we created the error; however, note that even if we have no clue where the error is, using this method allows us to determine the position of the error and correct it by simply flipping the bit.)

Because of the way the parity bits are positioned, an easier method to detect and correct the error bit is to add the positions of the parity bits that indicate an error. We found that parity bits 1 and 8 produced an error, and 1 + 8 = 9, which is exactly where the error occurred.

In the next chapter, you will see how easy it is to implement a Hamming code using simple binary circuits. Because of their simplicity, Hamming code protection can be added inexpensively and with minimal impact upon performance.

2.8.3 Reed-Soloman

Hamming codes work well in situations where one can reasonably expect errors to be rare events. Fixed magnetic disk drives have error ratings on the order of 1 bit in 100 million. The 3-bit Hamming code that we just studied will easily correct this type of error. However, Hamming codes are useless in situations where there is a likelihood that multiple adjacent bits will be damaged. These kinds of errors are called burst errors. Because of their exposure to mishandling and environmental stresses, burst errors are common on removable media such as magnetic tapes and compact disks.

If we expect errors to occur in blocks, it stands to reason that we should use an error-correcting code that operates at a block level, as opposed to a Hamming code, which operates at the bit level. A Reed-Soloman (RS) code can be thought of as a CRC that operates over entire characters instead of only a few bits. RS codes, like CRCs, are systematic: The parity bytes are appended to a block of information bytes. RS(n, k) codes are defined using the following parameters:

s = The number of bits in a character (or “symbol”)
k = The number of s-bit characters comprising the data block
n = The number of bits in the code word

RS(n, k) can correct errors in the k information bytes.

The popular RS(255, 223) code, therefore, uses 223 8-bit information bytes and 32 syndrome bytes to form 255-byte code words. It will correct as many as 16 erroneous bytes in the information block.

The generator polynomial for a Reed-Soloman code is given by a polynomial defined over an abstract mathematical structure called a Galois field. (A lucid discussion of Galois mathematics would take us far afield. See the references at the end of the chapter.) The Reed-Soloman generating polynomial is:

g(x) = (x aⁱ)(x aⁱ⁺¹) . . . (x a^i+2t)

where t = n k and x is an entire byte (or symbol) and g(x) operates over the field GF(2^s). (Note: This polynomial expands over the Galois field, which is considerably different from the integer fields used in ordinary algebra.)

The n-byte RS code word is computed using the equation:

c(x) = g(x) i(x)

where i(x) is the information block.

Despite the daunting algebra behind them, Reed-Soloman error-correction algorithms lend themselves well to implementation in computer hardware. They are implemented in high-performance disk drives for mainframe computers as well as compact disks used for music and data storage. These implementations will be described in Chapter 7.

Chapter Summary

We have presented the essentials of data representation and numerical operations in digital computers. You should master the techniques described for base conversion and memorize the smaller hexadecimal and binary numbers. This knowledge will be beneficial to you as you study the remainder of this book. Your knowledge of hexadecimal coding will be useful if you are ever required to read a core (memory) dump after a system crash or if you do any serious work in the field of data communications.

You have also seen that floating-point numbers can produce significant errors when small errors are allowed to compound over iterative processes. There are various numerical techniques that can be used to control such errors. These techniques merit detailed study but are beyond the scope of this book.

You have learned that most computers use ASCII or EBCDIC to represent characters. It is generally of little value to memorize any of these codes in their entirety, but if you work with them frequently, you will find yourself learning a number of “key values” from which you can compute most of the others that you need.

Unicode is the default character set used by Java and recent versions of Windows. It is likely to replace EBCDIC and ASCII as the basic method of character representation in computer systems; however, the older codes will be with us for the foreseeable future, owing both to their economy and their pervasiveness.

Your knowledge of how bytes are stored on disks and tape will help you to understand many of the issues and problems relating to data storage. Your familiarity with error control methods will aid you in your study of both data storage and data communications. You will learn more about data storage in Chapter 7. Chapter 11 presents topics relating to data communications.

Error-detecting and correcting codes are used in virtually all facets of computing technology. Should the need arise, your understanding of the various error control methods will help you to make informed choices among the various options available. The method that you choose will depend on a number of factors including computational overhead and the capacity of the storage and transmission media available to you.

Review Of Essential Terms And Concepts

The word bit is a contraction for what two words?
Explain how the terms bit, byte, nibble, and word are related.
Why are binary and decimal called positional numbering systems?
What is a radix?
How many of the “numbers to remember” (in all bases) from Figure 2.1 can you remember?
What does overflow mean in the context of unsigned numbers?
Name the three ways in which signed integers can be represented in digital computers and explain the differences.
Which one of the three integer representations is used most often by digital computer systems?
How are complement systems like the odometer on a bicycle?
Do you think that double-dabble is an easier method than the other binary-to-decimal conversion methods explained in this chapter? Why?
With reference to the previous question, what are the drawbacks of the other two conversion methods?
What is overflow and how can it be detected? How does overflow in unsigned numbers differ from overflow in signed numbers?
If a computer is capable only of manipulating and storing integers, what difficulties present themselves? How are these difficulties overcome?
What are the three component parts of a floating-point number?
What is a biased exponent, and what efficiencies can it provide?
What is normalization and why is it necessary?
Why is there always some degree of error in floating-point arithmetic when performed by a binary digital computer?
How many bits long is a double-precision number under the IEEE-754 floating-point standard?
What is EBCDIC, and how is it related to BCD?
What is ASCII and how did it originate?
How many bits does a Unicode character require?
Why was Unicode created?
Why is non-return-to-zero coding avoided as a method for writing data to a magnetic disk?
Why is Manchester coding not a good choice for writing data to a magnetic disk?
Explain how run-length-limited encoding works.
How do cyclic redundancy checks work?
What is systematic error detection?
What is a Hamming code?
What is meant by Hamming distance and why is it important? What is meant by minimum Hamming distance?
How is the number of redundant bits necessary for code related to the number of data bits?
What is a burst error?
Name an error detection method that can compensate for burst errors.

Exercises

Hints and Answers Perform the following base conversions using subtraction or division-remainder:
1. Hints and Answers 458₁₀ = ________ ₃
2. Hints and Answers 677₁₀ = ________ ₅
3. Hints and Answers 1518₁₀ = _______ ₇
4. Hints and Answers 4401₁₀ = _______ ₉
Perform the following base conversions using subtraction or division-remainder:
1. 588₁₀ = _________ ₃
2. 2254₁₀ = ________ ₅
3. 652₁₀ = ________ ₇
4. 3104₁₀ = ________ ₉
Hints and Answers Convert the following decimal fractions to binary with a maximum of six places to the right of the binary point:
1. Hints and Answers 26.78125
2. Hints and Answers 194.03125
3. Hints and Answers 298.796875
4. Hints and Answers 16.1240234375
Convert the following decimal fractions to binary with a maximum of six places to the right of the binary point:
1. 25.84375
2. 57.55
3. 80.90625
4. 84.874023
Represent the following decimal numbers in binary using 8-bit signed magnitude, one’s complement, and two’s complement:
1. Hints and Answers 77
2. Hints and Answers 42
3. 119
4. 107
Using a “word” of 3 bits, list all of the possible signed binary numbers and their decimal equivalents that are representable in:
1. Signed magnitude
2. One’s complement
3. Two’s complement
Using a “word” of 4 bits, list all of the possible signed binary numbers and their decimal equivalents that are representable in:
1. Signed magnitude
2. One’s complement
3. Two’s complement
From the results of the previous two questions, generalize the range of values (in decimal) that can be represented in any given x number of bits using:
1. Signed magnitude
2. One’s complement
3. Two’s complement
Given a (very) tiny computer that has a word size of 6 bits, what are the smallest negative numbers and the largest positive numbers that this computer can represent in each of the following representations?
1. Hints and Answers One’s complement
2. Two’s complement
You have stumbled on an unknown civilization while sailing around the world. The people, who call themselves Zebronians, do math using 40 separate characters (probably because there are 40 stripes on a zebra). They would very much like to use computers, but would need a computer to do Zebronian math, which would mean a computer that could represent all 40 characters. You are a computer designer and decide to help them. You decide the best thing is to use BCZ, Binary-Coded Zebronian (which is like BCD except it codes Zebronian, not Decimal). How many bits will you need to represent each character if you want to use the minimum number of bits?
Perform the following binary multiplications:
Perform the following binary multiplications:
Perform the following binary divisions:
1. Hints and Answers 101101 ÷ 101
2. 10000001 ÷ 101
3. 1001010010 ÷ 1011
Perform the following binary divisions:
1. 11111101 ÷ 1011
2. 110010101 ÷ 1001
3. 1001111100 ÷ 1100
Hints and Answers Use the double-dabble method to convert 10212₃ directly to decimal. (Hint: you have to change the multiplier.)
Using signed-magnitude representation, complete the following operations:

+ 0 + (-0) =

(-0) + 0 =

0 + 0 =

(-0) + (-0) =
Hints and Answers Suppose a computer uses 4-bit one’s complement numbers. Ignoring overflows, what value will be stored in the variable j after the following pseudocode routine terminates?
```
0  ®  j  // Store 0 in j.
-3  ®  k  // Store -3 in k.
while k ≠ 0
  j = j + 1
  k = k - 1
end while 
```
If the floating-point number storage on a certain system has a sign bit, a 3-bit exponent, and a 4-bit significand:
1. What is the largest positive and the smallest negative number that can be stored on this system if the storage is normalized? (Assume no bits are implied, there is no biasing, exponents use two’s complement notation, and exponents of all zeros and all ones are allowed.)
2. What bias should be used in the exponent if we prefer all exponents to be nonnegative? Why would you choose this bias?
Hints and Answers Using the model in the previous question, including your chosen bias, add the following floating-point numbers and express your answer using the same notation as the addend and augend:

Calculate the relative error, if any, in your answer to the previous question.
Assume we are using the simple model for floating-point representation as given in this book (the representation uses a 14-bit format, 5 bits for the exponent with a bias of 16, a normalized mantissa of 8 bits, and a single sign bit for the number):
1. Show how the computer would represent the numbers 100.0 and 0.25 using this floating-point format.
2. Show how the computer would add the two floating-point numbers in part a by changing one of the numbers so they are both expressed using the same power of 2.
3. Show how the computer would represent the sum in part b using the given floating-point representation. What decimal value for the sum is the computer actually storing? Explain.
What causes divide underflow and what can be done about it?
Why do we usually store floating-point numbers in normalized form? What is the advantage of using a bias as opposed to adding a sign bit to the exponent?
Let a = 1.0 x 2⁹, b = -1.0 x 2⁹ and c = 1.0 x 2¹. Using the floating-point model described in the text (the representation uses a 14-bit format, 5 bits for the exponent with a bias of 16, a normalized mantissa of 8 bits, and a single sign bit for the number), perform the following calculations, paying close attention to the order of operations. What can you say about the algebraic properties of floating-point arithmetic in our finite model? Do you think this algebraic anomaly holds under multiplication as well as addition?

b + (a + c) =

(b + a) + c =
1. Given that the ASCII code for A is 1000001, what is the ASCII code for J?
2. Given that the EBCDIC code for A is 1100 0001, what is the EBCDIC code for J?
Hints and Answers Assume a 24-bit word on a computer. In these 24 bits, we wish to represent the value 295.
1. Hints and Answers If our computer uses even parity, how would the computer represent the decimal value 295?
2. Hints and Answers If our computer uses 8-bit ASCII and even parity, how would the computer represent the string 295?
3. Hints and Answers If our computer uses packed BCD, how would the computer represent the number +295?
Decode the following ASCII message, assuming 7-bit ASCII characters and no parity: 1001010 1001111 1001000 1001110 0100000 1000100 1000101
Hints and Answers Why would a system designer wish to make Unicode the default character set for their new system? What reason(s) could you give for not using Unicode as a default?
Write the 7-bit ASCII code for the character 4 using the following encoding:
1. Non-return-to-zero
2. Non-return-to-zero-invert
3. Manchester code
4. Frequency modulation
5. Modified frequency modulation
6. Run length limited
  
  (Assume 1 is “high,” and 0 is “low.”)
Why is NRZ coding seldom used for recording data on magnetic media?
Assume we wish to create a code using 3 information bits, 1 parity bit (appended to the end of the information), and odd parity. List all legal code words in this code. What is the Hamming distance of your code?
Are the error-correcting Hamming codes systematic? Explain.
Hints and Answers Compute the Hamming distance of the following code:

0011010010111100

0000011110001111

0010010110101101

0001011010011110
Compute the Hamming distance of the following code:

0000000101111111

0000001010111111

0000010011011111

0000100011101111

0001000011110111

0010000011111011

0100000011111101

1000000011111110
Suppose we want an error-correcting code that will allow all single-bit errors to be corrected for memory words of length 10.
1. How many parity bits are necessary?
2. Assuming we are using the Hamming algorithm presented in this chapter to design our error-correcting code, find the code word to represent the 10-bit information word: 1001100110.
Hints and Answers Suppose we are working with an error-correcting code that will allow all single-bit errors to be corrected for memory words of length 7. We have already calculated that we need 4 check bits, and the length of all code words will be 11. Code words are created according to the Hamming algorithm presented in the text. We now receive the following code word:

1 0 1 0 1 0 1 1 1 1 0

Assuming even parity, is this a legal code word? If not, according to our error-correcting code, where is the error?
Repeat exercise 35 using the following code word:

0 1 1 1 1 0 1 0 1 0 1
Name two ways in which Reed-Soloman coding differs from Hamming coding.
When would you choose a CRC code over a Hamming code? A Hamming code over a CRC?
Hints and Answers Find the quotients and remainders for the following division problems modulo 2.
1. Hints and Answers 1010111₂ ÷ 1101₂
2. Hints and Answers 1011111₂ ÷ 11101₂
3. Hints and Answers 1011001101₂ ÷ 10101₂
4. Hints and Answers 111010111₂ ÷ 10111₂
Find the quotients and remainders for the following division problems modulo 2.
1. 1111010₂ ÷ 1011₂
2. 1010101₂ ÷ 1100₂
3. 1101101011₂ ÷ 10101₂
4. 1111101011₂ ÷ 101101₂
Hints and Answers Using the CRC polynomial 1011, compute the CRC code word for the information word, 1011001. Check the division performed at the receiver.
Using the CRC polynomial 1101, compute the CRC code word for the information word, 01001101. Check the division performed at the receiver.
* Pick an architecture (such as 80486, Pentium, Pentium IV, SPARC, Alpha, or MIPS). Do research to find out how your architecture approaches the concepts introduced in this chapter. For example, what representation does it use for negative values? What character codes does it support?