9.1. INTRODUCTION
So far we have considered that resistances, leakage and magnetization inductances are invariable with load.
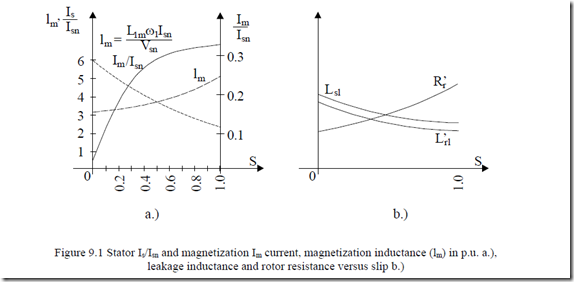
In reality, the magnetization current Im varies only slightly from no-load to full load (from zero slip to rated slip Sn ≈ 0.01 – 0.06), so the magnetization inductance L1m varies little in such conditions.
However, as the slip increases toward standstill, the stator current increases up to (5.5 – 6.5) times rated current at stall (S = 1).
In the same time, as the slip increases, even with constant resistances and leakage inductances, the magnetization current Im decreases.
So the magnetization current decreases while the stator current increases when the slip increases (Figure 9.1).
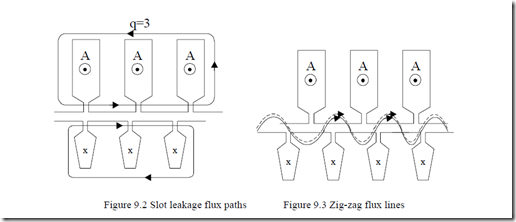
When the rotor (stator) current increases with slip, the leakage magnetic field path in iron tends to saturate. With open slots on stator, this phenomenon is limited, but, with semiopen or semiclosed slots, the slot leakage flux path saturates the tooth tops both in the stator and rotor (Figure 9.2) above (2−3) times rated current.
Also, the differential leakage inductance which is related to main flux path is affected by the tooth top saturation caused by the circumpherential flux produced by slot leakage flux lines (Figure 9.2). As the space harmonics flux
Further on, for large values of stator (and rotor) currents, the zig-zag flux becomes important and contributes notably to teeth top magnetic saturation in addition to slot leakage flux contribution.
Rotor slot skewing is also known to produce variable main flux path saturation along the stack length together with the magnetization current. However the flux densities from the two contributions are phase shifted by an angle which varies and increases towards 900 at standstill. The skewing contribution to the main flux path saturation increases with slip and dominates the picture for S > Sk as the magnetization flux density, in fact, decreases with slip so that at standstill it is usually 55 to 65% of its rated value.
A few remarks are in order.
• The magnetization saturation level in the core decreases with slip, such that at standstill only 55 – 65% of rated airgap flux remains.
• The slot leakage flux tends to increase with slip (current) and saturates the tooth top unless the slots are open.
• Zig – zag circumpherential flux and skewing accentuate the magnetic saturation of teeth top and of entire main flux path, respectively, for high currents (above 2 to 3 times rated current).
• The differential leakage inductance is also reduced when stator (and rotor) current increases as slot, zig-zag, and skewing leakage flux effects increase.
• As the stator (rotor) current increases the main (magnetising) inductance and leakage inductances are simultaneously influenced by saturation. So leakage and main path saturation are not independent of each other. This is why we use the term: on-load saturation.
As expected, accounting for these complex phenomena simultaneously is not an easy tractable mathematical endeavour. Finite element or even refined analytical methods may be suitable. Such methods are presented in this chapter after more crude approximations ready for preliminary design are given.
Besides magnetic saturation, skin (frequency) effect influences both the resistances and slot leakage inductances. Again, a simultaneous treatment of both aspects may be practically done only through FEM.
On the other hand, if slot leakage saturation occurs only on the teeth top and the teeth, additional saturation due to skewing does not influence the flux lines distribution within the slot, the two phenomena can be treated separately. Experience shows that such an approximation is feasible. Skin effect is treated separately for the slot body occupied by a conductor. Its influence on equivalent resistance and slot body leakage geometrical permeance is accounted for by two correction coefficients, KR and KX. The slot neck geometry is corrected for leakage saturation.
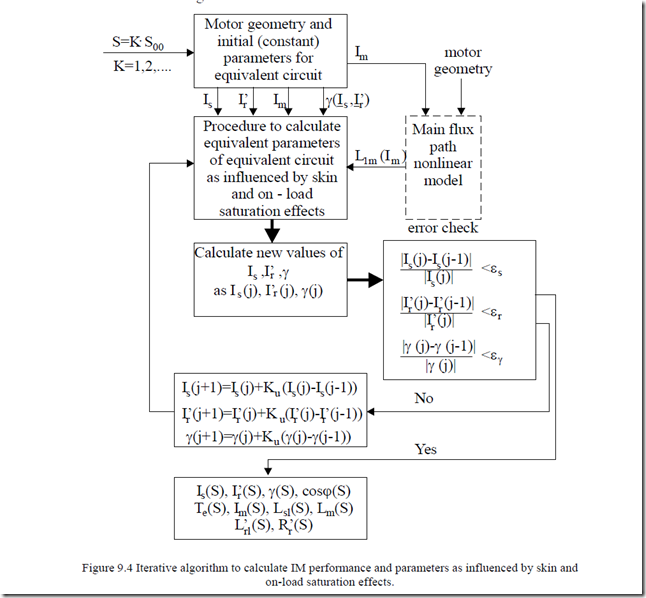
Finally, the on load saturation effects are treated iteratively for given slip values to find, from the equivalent circuit with variable parameters, the steady state performance. The above approach may be summarized as in Figure 9.4. The procedure starts with the equivalent circuit with constant parameters and calculates initial values of stator and rotor currents Is, Ir′ and their phase shift angle γ. Now that we described the whole picture, let us return to its different facets and start with skin effect.
9.2. THE SKIN EFFECT
As already mentioned, skin effects are related to the flux and current density distribution in a conductor (or a group of conductors) flowed by a.c. currents and surrounded by a magnetic core with some airgaps.
Easy to use analytical solutions have been found essentially only for rectangular slots, but adaptation for related shapes has also become traditional. More general slots with notable skin effect (of general shape) have been so far treated through equivalent multiple circuits after slicing the conductor(s) in slots in a few elements.
A refined slicing of conductor into many sections may be solved only numerically, but within a short computation time. Finally, FEM may also be used to account for skin effect. First, we will summarize some standard results for rectangular slots.
9.2.1. Single conductor in rectangular slot
Rectangular slots are typical for the stator of large IMs and for wound rotors of the same motors. Trapezoidal (and rounded) slots are typical for low power motors.
The case of a single conductor in slot is (Figure 9.5) typical to single (standard) cage rotors and is commonplace in the literature. The main results are given here.
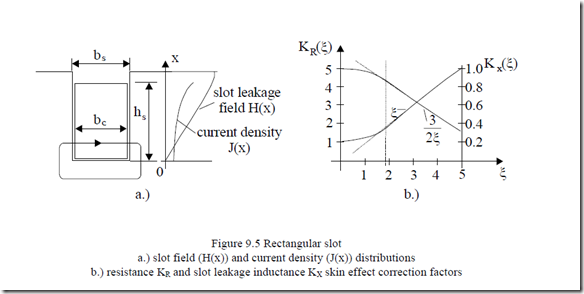
The correction coefficients for resistance and slot leakage inductance KR and KX are
![]() KR = ξ ((coshsinh 22ξ +ξ −sin 2cos2ξξ)) = RRdcac ; KX = 23ξ ((coshsinh 22ξ −ξ −sin 2cos2ξξ)) = ((LLslssls ))dcac (9.1) with ξ = βhs = δhAls ; β = δ1Al = Sω µ σ1 20 Al bbcs ; σAl − electrical conductivity (9.2)
KR = ξ ((coshsinh 22ξ +ξ −sin 2cos2ξξ)) = RRdcac ; KX = 23ξ ((coshsinh 22ξ −ξ −sin 2cos2ξξ)) = ((LLslssls ))dcac (9.1) with ξ = βhs = δhAls ; β = δ1Al = Sω µ σ1 20 Al bbcs ; σAl − electrical conductivity (9.2)
The slip S signifies that in this case the rotor (or secondary) of the IM is considered.
Figure 9.5 depicts KR and Kx as functions of ξ, which, in fact, represents the ratio between the conductor height and the field penetration depth δAl in the conductor for given frequency Sω1. With one conductor in the slot, the skin effects, as reflected in KR and Kx, increase with the slot (conductor) height, hs, for given slip frequency Sω1.
This rotor resistance increase, accompanied by slot leakage inductance (reactance) decrease, leads to both a lower starting current and a higher starting torque.
This is how the deep bar cage rotor has evolved. To increase further the skin effects, and thus increase starting torque for even lower starting current
(Istart = (4.5−5)Irated), the double cage rotor was introduced by the turn of this century already by Dolivo – Dobrovolski and later by Boucherot.
The advent of power electronics, however, has led to low frequency starts and thus, up to peak torque at start, may be obtained with (2.5−3) times rated current. Skin effect in this case is not needed. Reducing skin effect in large induction motors with cage rotors lead to particular slot shapes adequate for variable frequency supply.
9.2.2. Multiple conductors in rectangular slots: series connection
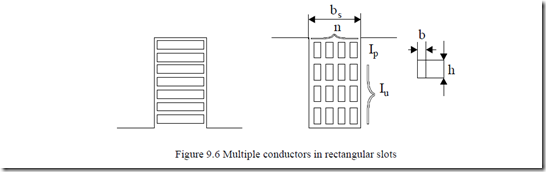
Multiple conductors are placed in the stator slots, or in the rotor slots of wound rotors (Figure 9.6).
According to Emde and R.Richter [1,2] who continued the classic work of Field [3], the resistance correction coefficient KRP for the pth layer in slot (Figure
9.6) with current Ip, when total current below pth layer is Iu, is
KRP = ϕ ξ +( ) Iu (I cosu Ip2γ + Ip )ψ ξ( ) (9.3)
ϕ ξ = ξ( ) ![]() ; ψ ξ =( ) 2ξ
; ψ ξ =( ) 2ξ![]() (9.4)
(9.4)
![]() ξ =βn h; β =n Sω µ σ1 20 Al nbbs
ξ =βn h; β =n Sω µ σ1 20 Al nbbs
There are n conductors in each layer and γ is the angle between Ip and Iu phasors.
In two-layer windings with chorded coils, there are slots where the current in all conductors is the same and some in which two phases are located and thus the currents are different (or there is a phase shift γ = 600). For the case of γ = 0 with Iu = Ip(p – 1) Equation (9.3) becomes
KRP = ϕ ξ +( ) (p2 − p)ψ ξ( ) (9.5)
This shows that the skin effect is not the same in all layers. The average value of KRP for m layers,
KRm = m1 ∑m KRP( )p = ϕ ξ +( ) m23−1ψ ξ >( ) 1 (9.6)
1
Based on [4], for γ ≠ 0 in (9.6) (m2−1)/3 is replaced by
24
A similar expression is obtained for the slot-body leakage inductance correction Kx [4].
Kxm = ϕ ξ +'( ) (m2 −m12)ψ ξ'( ) <1 (9.7)
ϕ ξ ='( ) ![]() (9.8) ψ ξ ='( )
(9.8) ψ ξ ='( ) ![]() (9.9)
(9.9)
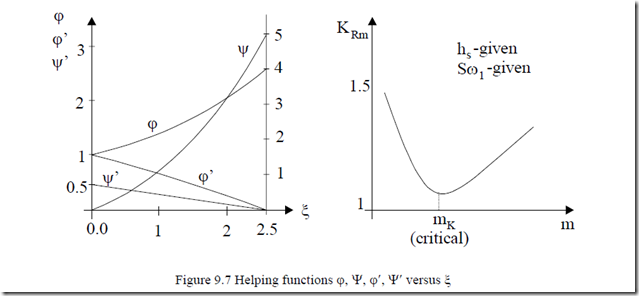
Please note that the first terms in KRm and Kxm are identical to KR and Kx of (9.1) valid for a single conductor in slot. As expected, KRm and Kxm degenerate into KR and Kx for one layer (conductor) per slot. The helping functions ϕ, ψ, ϕ′, ψ′ are quite general (Figure 9.7).
For a given slot geometry, increasing the number of conductor layers in slot reduces their height h = hs/m and thus reduces ξ, which ultimately reduces ψ(ξ) in (9.6). On the other hand, increasing the number of layers, the second term in (9.6) tends to increase.
It is thus evident that there is a critical conductor height hc for which the resistance correction coefficient is minimum. Reducing the conductor height below hc does not produce a smaller KRm.
In large power or in high speed (frequency), small/medium power machines this problem of critical conductor height is of great importance to minimize the additional (a.c.) losses in the windings.
A value of KRm ≈ (1.1 – 1.2) is in most cases, acceptable. At power grid frequency (50 – 60 Hz), the stator skin effect resistance correction coefficient is very small (close to 1.0) as long as power is smaller than a few hundred kW. Inverter-fed IMs, however, show high frequency time harmonics for which KRm may be notable and has to be accounted for.
Example 9.1. Derivation of resistance and reactance corrections
Let us calculate the magnetic field H(x) and current density J(x) in the slot of an IM with m identical conductors (layers) in series making a single layer winding.
Solution
To solve the problem we use the field equation in complex numbers for the slot space where only along slot depth (OX) the magnetic field and current density vary.