Accelerometer systems
For sensing the quantities of acceleration, velocity and distance travelled, systems based on accelerometers are used. The basis of all accelerometers is the action of acceleration on a mass to produce force, following the equation F = Ma where F is force measured in newtons, M is mass in kilograms and a is acceleration in units of mjs2. The use of a mass, often termed an inertiaL mass, in this way is complicated by the effect of the acceleration of gravity which causes any mass to exert a force (its weight) that is directed towards the centre of the Earth. The mass that is used as part of an acceleration sensor must therefore be supported in the vertical plane, and the type of support that is used will depend on whether accelerations in this plane are to be measured.
• Accelerometers are widely used in vibration and shock measurements, particularly in studies of the effectiveness of packaging. This applies also
to car crash testing and to metering systems used to assess the performance of racing cars.
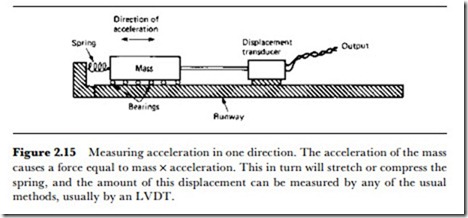
If the acceleration to be measured is always in a horizontal direction, then the mass can be supported on wheels, ball bearings or air-jets, depending on the sensitivity that is required. Since a force on the mass is to be sensed, the mass will also have to be coupled to a sensor. The method of sensing force is to measure the displacement of the mass against the restoring force of a spring, so that the outline system for a horizontal accelerometer is as sketched in Figure 2.15. The weight of the mass is supported on ball bearings, and the mass is held in the horizontal plane by springs. In Figure 2.15, acceleration in only one direction is to be measured, so that only one spring is illustrated, and it is assumed that sideways movements of the mass are restrained in some other way, by another set of springs or by guide rails. Vhen an acceleration in the chosen direction affects the mass, it will be displaced against the springs, extending one spring and compressing the other. The amount of linear movement will be proportional to the force, so that any sensor for linear displacement can be used to give an output that is proportional to acceleration. Suitable transducers include potentiometers, capacitive distance gauges, inductive gauges and LVDTs for the larger ranges of movement that are possible. Sensors for acceleration that use this spring and displacement principle are generally intended for the measurement of very small accelerations, usually in one plane.
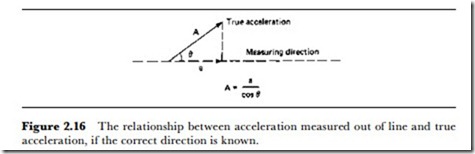
If only a single dimensional acceleration can be measured, the acceleration in any other direction will produce a false reading, equal to the component of acceleration in that direction. Figure 2.16 shows how this component of acceleration is related to the true value and to the angle between the true acceleration and the measured acceleration directions.
• If the mass can be supported in a cradle of springs and three displacement sensors connected, one for each axis of motion (two horizontal and one vertical), then the outputs can be used to compute the magnitude and direction of an acceleration that can be in any direction.
A strain-gauge sensor can be connected to an inertial mass, with or without spring suspension in order to measure acceleration, but the most common type of accelerometer uses an inertial mass coupled to a piezoelectric crystal. The piezoelectric effect has been known since the end of the 19th century, even though in 1960 one major University textbook of physics did not mention it. The principle is that some crystalline materials such as quartz (silicon oxide), Rochelle salt and barium titanate are composed of charged particles (ions) which do not move uniformly when the crystal is stressed. Because of this non-uniformity, movement of the ions produces a difference in charge between opposing faces of the crystal, and if these faces are metallized, a voltage can be measured. The voltage is proportional to the strain of the crystal and can be very large, of the order of kilovolts for some ceramic crystal types, if the strain of the crystal is large. This principle is used to provide a spark for cigarette lighters, gas fires, and gas or oil boiler ignition systems.
The use of an inertial mass bonded to a piezoelectric crystal therefore provides an accelerometer that requires no springs or special supports for the mass. It is even possible to obtain two-dimensional signals from one crystal, and the system will respond to a very wide range of accelerations.
Although the unit of acceleration is mjs2, acceleration is very often
measured relative to the ‘standard’ value of the acceleration of gravity, which is 9.81 mjs2. This leads to figures of acceleration in ‘g’ units, from which the value in scientific units can be calculated by multiplying by 9.81. Piezoelectric transducers can cope with acceleration values from a very small fraction of ‘g’ to several thousand ‘g’, a huge range compared to those that can be obtained by using spring and displacement systems. The snag is that the piezoelectric crystal is, from the circuit point of view, a capacitor, and the signal is in the form of a charge. The connection of a resistance to the contacts on the faces of the crystal will therefore allow this capacitance to discharge with a time constant equal to CR seconds, where C is the capacitance between the crystal faces in JlF and R is the resistance between the faces in Ml. If, for example, the capacitance is 1000 pF (= 0.001 JlF) and the resistance is 10000 Ml (the input of a FET DC amplifier, perhaps), then the time constant is only 10 s. This makes the piezoelectric type of sensor more suitable for measuring changes of acceleration that occur over a short time, perhaps a fraction of a second, than for measuring fairly constant values of acceleration for a long period.
As it happens, most accelerations are not sustained. Newton’s first law states in effect that the natural state of any object in the universe is uniform motion in a straight line with no form of acceleration, and acceleration comes about only because of force. The only steady and constant value of acceleration that we normally encounter is the acceleration of gravity, and most of our acceleration measurements are on accelerations that are caused by short-duration forces, such as those encountered when one object hits another. To put this into perspective, an acceleration of only 1 g for 10 s corresponds to falling a distance of about 500 m in a vacuum. In general, unless you are working with propulsion systems for outer space, the measurement of small accelerations that are applied for long periods will be of no practical interest.
Vhen an accelerometer of any type produces an electrical output, this output can be used for computing other quantities. One of these quantities is speed or, more correctly, veLocity because an acceleration exists when a change of direction or a change of speed, or both, take place. The relation- ship between speed or velocity value and acceleration is shown in Figure 2.17, so that if the starting speed of an object, its acceleration (assumed constant) and the time of acceleration are all known, then the final speed can be calculated.
The mathematical action needed to find change of speed from acceleration and time is called integration, and analogue computers can carry out this action on a voltage signal from an accelerometer. The initial speed can be set in the form of a voltage applied from a potentiometer, and the output of the analogue computer is proportional to final speed. A second integration of the voltage output (the speed output) will produce a signal proportional to distance, so that this quantity can also be found by using an analogue computing action on the output of the accelerometer. If the starting point of the motion is rest (no starting speed), then no constants need to be fed in. The analogue computer can consist of little more than a pair of operational amplifiers if a simple one-dimensional motion is being sensed. If quantities are expressed in digital terms, then a digital computer can be used to calculate the integral values.