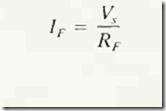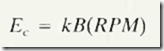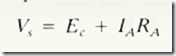In most industrial situations. motors are operated directly from the ac or de supply lines. That is, the motor winding terminal s are connected directly to the lines which supply the electric current. In these situation s, the operating behavior of the motor is determined by the nature of the mechanical load connected to the motor’s shaft. In simple term s. if the load is easy to drive. the motor will tend to deliver relatively little torque , and it will run at a high speed. If the load is difficult to drive, the motor will tend to deliver a lot of torqu e. and it will run at a lower speed. The point is that the operating behavior of th e motor is set by it s load (for a fixed supply line voltage). and the operator has no control over motor behavior.
In modern industrial situations, there are many applications which require that the operator be able to intervene t o control th e motor speed. Such contro l is u sually accomp li shed with thyri stor s. The combination of the motor , the controllin g thyristor( s) , and the associated electronic components is referred to as a speed control systc111 or a drit ·e sys tem.
OBJECTIVES
After compl etmg this ch apte r . you will be able to:
I. Explain the two basic method of adjuting the speed of a de shunt motor.
2.Discuss the relative advantages and disadvantages of speed adjustment of a de motor from th e field a nd from the armature.
3. Explain why armature control with thyristors is superior to all other de motor speed
control methods.
4 . Discuss how counter-EMF feedback can ·be used to improve a motor’s load regulation.
5. Calculate a motor’s load regulation, given a graph of shaft speed versus load torque
(or horsepower).
6. Expla in the operation of th e single-pha se and three-phase thyristor drive systems which
are presented.
7. Explain the operation of a switchgear-co ntrolled rever sible drive system.
8 . For a three-phase inverter circuit. analyze the SCR swit ching schedule and relate it
to the three-phase ac output waveforms.
9. Recognize the necessity for forced commut ation of th e SCRs in a dc-to-ac inverter , and describe the operation of the method that is presented.
10. For an ac drive system, explain why the voltage ma gnitude must be varied in proportion to the frequency: show how this can be accomplish ed by combining a variable rectifier with an inverter.
11. For a 6- or 12-SCR single-pha se cycloconverter, describe the SCR switching sequence
ami relate it to the ac output waveform.
12. Describe the techniqu es for improving the output waveshape of a cycloconverter.
13. Show how three single-ph ase cycloconverte:s are connected to drive a three-phase motor.
15-1 DC MOTORS-OPERATION AND CHARACTERISTICS
De motors are important in indu strial control because they are more adaptable than rotating-field ac motors to adjustable speed systems.
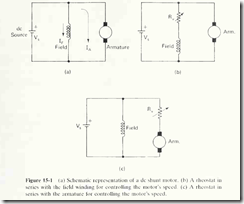
Figure 15-1 shows the schematic symbol of a de shunt motor. The motor’s
field winding is drawn as a coil. Physically, the field winding is composed of many turns of thin (high-resistance) wire wrapped around the field poles. The field poles are ferromagnetic metal cores. which are attached to the stator of the machine. The high resistance of the field winding limits the field current to a fairly small value, allowing the field winding to be connected directly across the de supply lines. However, the relatively small field current (IF) is compensated for by the field winding’s large number of turns. enabling the winding to create a strong magnetic field.
The field winding is unaffected by cha nging conditions in the armature. That is. as the armature current varies t o meet varying load conditions. the field winding current stays essentially constant, and the strength of the resulting magnetic field stays constant. The field current can be found easily from Ohm’s law as
where vs, i s the source voltage applied to the field winding [Fig. 15- 1(a)j and RF is the winding ‘s de resistance .
The armature winding i s shown in Fig. 15-l(a) as a circle contacted by two small squares. It is drawn like this beca u se th e a rmatur e winding is constructed on the cylindrical rotor of the machin e and current is carried to and from the armature winding via carbon bru shes contacting commutator segmen t s.
The armature winding of a de motor is constructed of relatively few turns of thicker wire, so it has a low de resi stance . The armature winding resistance of a
medium- or large-sized de motor i s usually less th an 1 ohm.
When power is first applied to the armature winding, only the de ohmic resistance of the winding i s available to limit th e current. so th e inrush current surge is quite great. However , as th e m otor begins to accelerate, it begins to induce (generate) a countcr-EAIF by the u sua l gen erator action. This counter-EMF op poses the applied source voltage and limit s th e armatur e curr ent to a reasonable value.
When a de motor has reached normal operating speed, its counter-EMF is about t}() ”c as grea t as the a ppli ed armature voltage vs, in Fig. 15- 1 (a)]. The I R
voltage drop across the armature winding resistance accounts for the other 10% of th e applie voltage, neglecting any voltage drop across the carbon brushes.
The exact size of the counter-EMF ‘generated by the armature winding depends on two things:
I. The strength of the magnetic field. The stronger the magnetic field, the greater th e counter-EMF tend s t o be.
2. The speed of rotation. The greater the speed, the greater the counter-EMF tends to be .
Equation (15-2) expresses the dependence of counter-EMF on field strength and rota ti onal speed:
In Eq. (15-2). Ec stands for the counter-EMF created by the spinning armature windin g, B stands for th e strength of the magnetic field created by the field winding, and RPM i s the rotational speed in revolutions per minut e. The proportionality constant k depends on the construc ti on details of the armature (the number of winJing turns. th e length of the conductor s. etc.) .
Kirchhoff’s voltage law for the armature loop is expressed in Eq. (15-3), which simply state s that th e applied armature voltage is equal to the sum of the voltage drops in the armatur e. The sum of the voltage drops in the armature winding equals th e counter-EMF added to the IR resistive voltage drop, again neglecting the min or effect of th e brush drop .
In Eq . (15-3), RA stand s for the de resistance of the armature winding, and of course I A is th e armature current.